| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
D.61 Chemical potential in the distributions
The following convoluted derivation of the distribution functions
comes fairly straightly from Baierlein [4, pp. 170-].
Let it not deter you from reading the rest of this otherwise very
clearly written and engaging little book. Even a nonengineering
author should be allowed one mistake.
The derivations of the Maxwell-Boltzmann, Fermi-Dirac, and
Bose-Einstein distributions given previously, {D.57}
and {D.58}, were based on finding the most numerous or
most probable distribution. That implicitly assumes that significant
deviations from the most numerous/probable distributions will be so
rare that they can be ignored. This note will bypass the need for
such an assumption since it will directly derive the actual
expectation values of the single-particle state occupation numbers
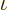 . In particular for fermions, the derivation will be
solid as a rock.
. In particular for fermions, the derivation will be
solid as a rock.
The mission is to derive the expectation number 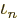 of particles
in an arbitrary single-particle state
of particles
in an arbitrary single-particle state 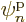 . This
expectation value, as any expectation value, is given by the possible
values times their probability:
. This
expectation value, as any expectation value, is given by the possible
values times their probability:
where 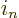 is the number of particles that system energy
eigenfunction
is the number of particles that system energy
eigenfunction 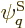 has in single-particle state
has in single-particle state
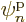 , and
, and 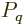 the probability of the eigenfunction.
Since thermal equilibrium is assumed, the canonical probability value
the probability of the eigenfunction.
Since thermal equilibrium is assumed, the canonical probability value
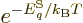

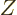 can be substituted for
can be substituted for 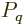 . Then, if
the energy
. Then, if
the energy 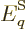 is written as the sum of the ones of the single
particle states times the number of particles in that state, it gives:
is written as the sum of the ones of the single
particle states times the number of particles in that state, it gives:
Note that 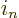 is the occupation number of single-particle state
is the occupation number of single-particle state
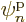 , just like
, just like 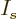 was the occupation number of shelf
was the occupation number of shelf
 . Dealing with single-particle state occupation numbers has
an advantage over dealing with shelf numbers: you do not have to
figure out how many system eigenfunctions there are. For a given set
of single-particle state occupation numbers
. Dealing with single-particle state occupation numbers has
an advantage over dealing with shelf numbers: you do not have to
figure out how many system eigenfunctions there are. For a given set
of single-particle state occupation numbers 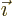

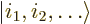 , there is exactly one system
energy eigenfunction. Compare figures 11.2 and
11.3: if you know how many particles there are in each
single-particle state, you know everything there is to know about the
eigenfunction depicted. (This does not apply to distinguishable
particles, figure 11.1, because for them the numbers on
the particles can still vary for given occupation numbers, but as
noted in chapter 11.11, there is no such thing as identical
distinguishable particles anyway.)
, there is exactly one system
energy eigenfunction. Compare figures 11.2 and
11.3: if you know how many particles there are in each
single-particle state, you know everything there is to know about the
eigenfunction depicted. (This does not apply to distinguishable
particles, figure 11.1, because for them the numbers on
the particles can still vary for given occupation numbers, but as
noted in chapter 11.11, there is no such thing as identical
distinguishable particles anyway.)
It has the big consequence that the sum over the eigenfunctions can be
replaced by sums over all sets of occupation numbers:
Each set of single-particle state occupation numbers corresponds to
exactly one eigenfunction, so each eigenfunction is still counted
exactly once. Of course, the occupation numbers do have to add up to
the correct number of particles in the system.
Now consider first the case of  identical bosons. For them the
occupation numbers may have values up to a maximum of I:
identical bosons. For them the
occupation numbers may have values up to a maximum of I:
One simplification that is immediately evident is that all the terms
that have 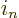
 0 are zero and can be ignored. Now apply a
trick that only a mathematician would think of: define a new summation
index
0 are zero and can be ignored. Now apply a
trick that only a mathematician would think of: define a new summation
index 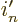 by setting
by setting 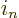

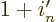 . Then the
summation over
. Then the
summation over 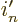 can start at 0 and will run up to
can start at 0 and will run up to  .
Plugging
.
Plugging 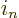

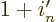 into the sum above gives
into the sum above gives
This can be simplified by taking the constant part of the exponential
out of the summation. Also, the constraint in the bottom shows that
the occupation numbers can no longer be any larger than  (since
the original
(since
the original 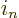 is at least one), so the upper limits can be
reduced to
is at least one), so the upper limits can be
reduced to  . Finally, the prime on
. Finally, the prime on 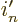 may as well be
dropped, since it is just a summation index and it does not make a
difference what name you give it. So, altogether,
may as well be
dropped, since it is just a summation index and it does not make a
difference what name you give it. So, altogether,
The right hand side falls apart into two sums: one for the 1 in
 and one for the
and one for the 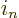 in
in  . The first sum is
essentially the partition function
. The first sum is
essentially the partition function 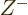 for a system with
for a system with  particles instead of
particles instead of  . The second sum is essentially
. The second sum is essentially 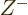 times the expectation value
times the expectation value 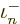 for such a system. To be
precise
for such a system. To be
precise
This equation is exact, no approximations have been made yet.
The system with  particles is the same in all respects to the one
for
particles is the same in all respects to the one
for  particles, except that it has one less particle. In
particular, the single-particle energy eigenfunctions are the same,
which means the volume of the box is the same, and the expression for
the canonical probability is the same, meaning that the temperature is
the same.
particles, except that it has one less particle. In
particular, the single-particle energy eigenfunctions are the same,
which means the volume of the box is the same, and the expression for
the canonical probability is the same, meaning that the temperature is
the same.
But when the system is macroscopic, the occupation counts for  particles must be virtually identical to those for
particles must be virtually identical to those for  particles.
Clearly the physics should not change noticeably depending on whether
10
particles.
Clearly the physics should not change noticeably depending on whether
10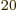 or 10
or 10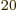 + 1 particles are present. If
+ 1 particles are present. If
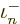

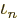 , then the above equation can be
solved to give:
, then the above equation can be
solved to give:
The final formula is the Bose-Einstein distribution with
Solve for  :
:
The final fraction is a difference quotient approximation for the
derivative of the Helmholtz free energy with respect to the number of
particles. Now a single particle change is an extremely small change
in the number of particles, so the difference quotient will be to very
great accuracy be equal to the derivative of the Helmholtz free energy
with respect to the number of particles. And as noted earlier, in the
obtained expressions, volume and temperature are held constant. So,


 , and
(11.39) identified that as the chemical potential. Do note
that
, and
(11.39) identified that as the chemical potential. Do note
that  is on a single-particle basis, while
is on a single-particle basis, while 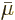 was taken to
be on a molar basis. The Avogadro number
was taken to
be on a molar basis. The Avogadro number 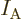
 6.022 1
10
6.022 1
10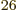 particles per kmol converts between the two.
particles per kmol converts between the two.
Now consider the case of  identical fermions. Then, according to
the exclusion principle, there are only two allowed possibilities for
the occupation numbers: they can be zero or one:
identical fermions. Then, according to
the exclusion principle, there are only two allowed possibilities for
the occupation numbers: they can be zero or one:
Again, all terms with 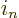
 0 are zero, so you can set
0 are zero, so you can set 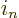

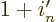 and get
and get
But now there is a difference: even for a system with  particles
particles
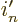 can still have the value 1 but the upper limit is zero.
Fortunately, since the above sum only sums over the single value
can still have the value 1 but the upper limit is zero.
Fortunately, since the above sum only sums over the single value
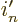
 0, the factor
0, the factor 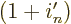 can be replaced by
can be replaced by  without
changing the answer. And then the summation can include
without
changing the answer. And then the summation can include 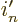
 1
again, because
1
again, because  is zero when
is zero when 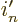
 1. This sign change
produces the sign change in the Fermi-Dirac distribution compared to
the Bose-Einstein one; the rest of the analysis is the same.
1. This sign change
produces the sign change in the Fermi-Dirac distribution compared to
the Bose-Einstein one; the rest of the analysis is the same.
Here are some additional remarks about the only approximation made,
that the systems with  and
and  particles have the same
expectation occupation numbers. For fermions, this approximation is
justified to the gills, because it can be easily be seen that the
obtained value for the occupation number is in between those of the systems with
particles have the same
expectation occupation numbers. For fermions, this approximation is
justified to the gills, because it can be easily be seen that the
obtained value for the occupation number is in between those of the systems with  and
and  particles.
Since nobody is going to count whether a macroscopic system has
10
particles.
Since nobody is going to count whether a macroscopic system has
10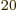 particles or 10
particles or 10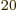 + 1, this is truly as good as
any theoretical prediction can possibly get.
+ 1, this is truly as good as
any theoretical prediction can possibly get.
But for bosons, it is a bit trickier because of the possibility of
condensation. Assume, reasonably, that when a particle is added, the
occupation numbers will not go down. Then the derived expression
overestimates both expectation occupation numbers 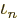 and
and
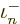 . However, it could at most be wrong, (i.e. have a
finite relative error) for a finite number of states, and the number
of single-particle states will be large. (In the earlier derivation
using shelf numbers, the actual
. However, it could at most be wrong, (i.e. have a
finite relative error) for a finite number of states, and the number
of single-particle states will be large. (In the earlier derivation
using shelf numbers, the actual 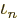 was found to be lower than
the Bose-Einstein value by a factor
was found to be lower than
the Bose-Einstein value by a factor 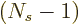

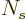 with
with 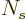 the
number of states on the shelf.)
the
number of states on the shelf.)
If the factor 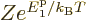

 is one exactly, which
definitely means Bose-Einstein condensation, then
is one exactly, which
definitely means Bose-Einstein condensation, then 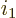

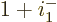 . In that case, the additional particle that the
system with
. In that case, the additional particle that the
system with  particles has goes with certainty into the ground
state. So the ground state better be unique then; the particle cannot
go into two ground states.
particles has goes with certainty into the ground
state. So the ground state better be unique then; the particle cannot
go into two ground states.
![]() .
.![]()
![]() .
.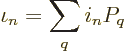
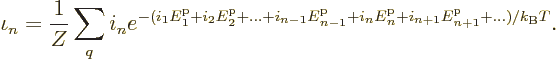
![]()
![]() ,
,![]()
![]() .
.![]()
![]()
![]() ,
,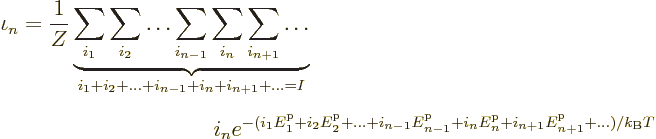
![]()
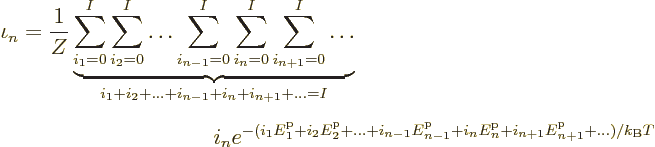
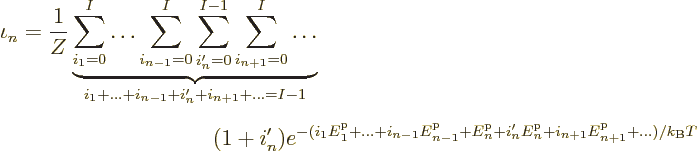

![]()
![]()
![]() .
.![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![\begin{displaymath}
\iota_n = 1\left/\left[\frac{Z}{Z^-} e^{{\vphantom' E}^{\rm p}_n/{k_{\rm B}}T} - 1 \right]\right.
\end{displaymath}](img7268.gif)
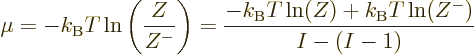
![]()
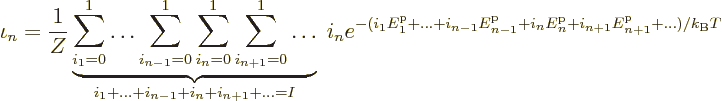
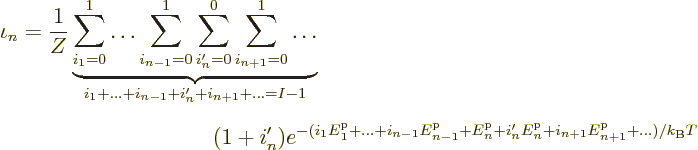
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()