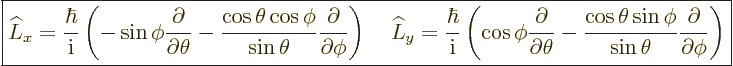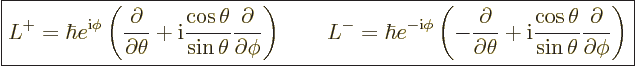| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
D.64 Spherical harmonics by ladder operators
One application of ladder operators is to find the spherical harmonics, which as noted in chapter 4.2.3 is not
an easy problem. To do it with ladder operators, show that
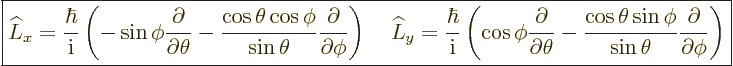 |
(D.41) |
then that
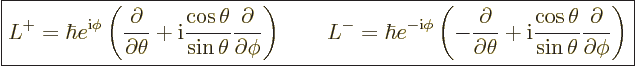 |
(D.42) |
Note that the spherical harmonics are of the form 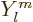

 , so
, so
Find the 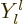 harmonic from
harmonic from 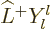
 0. That gives
0. That gives
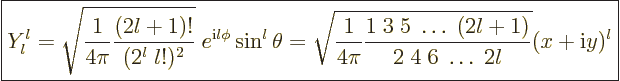 |
(D.43) |
Now apply 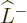 to find the rest of the ladder.
to find the rest of the ladder.
Interestingly enough, the solution of the one-dimensional harmonic
oscillator problem can also be found using ladder operators. It turns
out that, in the notation of that problem,
are commutator eigenoperators of the harmonic oscillator Hamiltonian,
with eigenvalues 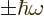 . So, you can play the same
games of constructing ladders. Easier, really, since there is no
equivalent to square angular momentum to worry about in that problem:
there is only one ladder. See [25, pp. 42-47] for
details. An equivalent derivation is given in addendum
{A.15.5} based on quantum field theory.
. So, you can play the same
games of constructing ladders. Easier, really, since there is no
equivalent to square angular momentum to worry about in that problem:
there is only one ladder. See [25, pp. 42-47] for
details. An equivalent derivation is given in addendum
{A.15.5} based on quantum field theory.