| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
Subsections
4.2 Angular Momentum
Before a solution can be found for the important electronic structure
of the hydrogen atom, the basis for the description of all the other
elements and chemical bonds, first angular momentum must be discussed.
Like in the classical Newtonian case, angular momentum is essential
for the analysis, and in quantum mechanics, angular momentum is also
essential for describing the final solution. Moreover, the quantum
properties of angular momentum turn out to be quite unexpected and
important for practical applications.
4.2.1 Definition of angular momentum
The old Newtonian physics defines angular momentum  as
the vectorial product
as
the vectorial product 

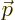 , where
, where  is the
position of the particle in question and
is the
position of the particle in question and 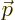 is its linear
momentum.
is its linear
momentum.
Following the Newtonian analogy, quantum mechanics substitutes
the gradient operator 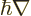

 for the linear momentum,
so the angular momentum operator becomes:
for the linear momentum,
so the angular momentum operator becomes:
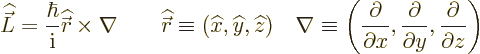 |
(4.18) |
Unlike the Hamiltonian, the angular momentum operator is not
specific to a given system. All observations about angular momentum
will apply regardless of the physical system being studied.
Key Points

- The angular momentum operator (4.18) has been
identified.
4.2.2 Angular momentum in an arbitrary direction
The intent in this subsection is to find the operator for the angular
momentum in an arbitrary direction and its eigenfunctions and
eigenvalues.
For convenience, the direction in which the angular momentum is
desired will be taken as the  -axis of the coordinate system. In
fact, much of the mathematics that you do in quantum mechanics
requires you to select some arbitrary direction as your
-axis of the coordinate system. In
fact, much of the mathematics that you do in quantum mechanics
requires you to select some arbitrary direction as your  -axis, even
if the physics itself does not have any preferred direction. It is
further conventional in the quantum mechanics of atoms and molecules
to draw the chosen
-axis, even
if the physics itself does not have any preferred direction. It is
further conventional in the quantum mechanics of atoms and molecules
to draw the chosen  -axis horizontal, (though not in
[25] or [52]), and that is what will be done
here.
-axis horizontal, (though not in
[25] or [52]), and that is what will be done
here.
Figure 4.7:
Spherical coordinates of an arbitrary point P.
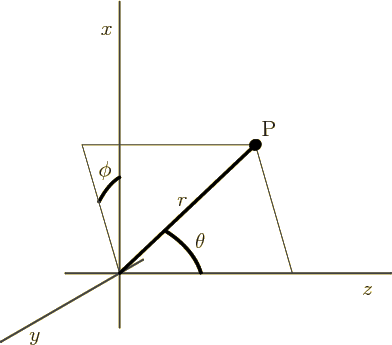 |
Things further simplify greatly if you switch from Cartesian
coordinates  ,
,  , and
, and  to “spherical coordinates”
to “spherical coordinates”  ,
,  , and
, and
 , as shown in figure 4.7. The coordinate
, as shown in figure 4.7. The coordinate  is the distance from the chosen origin,
is the distance from the chosen origin,  is the angular
position away from the chosen
is the angular
position away from the chosen  -axis, and
-axis, and  is the angular
position around the
is the angular
position around the  -axis, measured from the chosen
-axis, measured from the chosen  -axis.
-axis.
In terms of these spherical coordinates, the  -component of angular
momentum simplifies to:
-component of angular
momentum simplifies to:
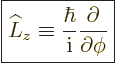 |
(4.19) |
This can be verified by looking up the gradient operator  in
spherical coordinates in [41, pp. 124-126] and then
taking the component of
in
spherical coordinates in [41, pp. 124-126] and then
taking the component of 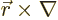 in the
in the  -direction.
-direction.
In any case, with a bit of thought, it clearly makes sense: the
 -component of linear momentum classically describes the
motion in the direction of the
-component of linear momentum classically describes the
motion in the direction of the  -axis, while the
-axis, while the
 -component of angular momentum describes the motion
around the
-component of angular momentum describes the motion
around the  -axis. So if in quantum mechanics the
-axis. So if in quantum mechanics the  linear momentum is
linear momentum is 

 times the derivative with respect
the coordinate
times the derivative with respect
the coordinate  along the
along the  -axis, then surely the logical
equivalent for
-axis, then surely the logical
equivalent for  angular momentum is
angular momentum is 

 times the
derivative with respect to the angle
times the
derivative with respect to the angle  around the
around the  -axis?
-axis?
Anyway, the eigenfunctions of the operator  above turn out to be
exponentials in
above turn out to be
exponentials in  . More precisely, the eigenfunctions are
of the form
. More precisely, the eigenfunctions are
of the form
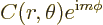 |
(4.20) |
Here  is a constant and
is a constant and 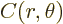 can be any arbitrary function
of
can be any arbitrary function
of  and
and  . For historical reasons, the number
. For historical reasons, the number  is
called the “magnetic quantum number”. Historically, physicists have never
seen a need to get rid of obsolete and confusing terms. The magnetic
quantum number must be an integer, one of
is
called the “magnetic quantum number”. Historically, physicists have never
seen a need to get rid of obsolete and confusing terms. The magnetic
quantum number must be an integer, one of
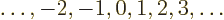 The reason is that if you increase the
angle
The reason is that if you increase the
angle  by
by  , you make a complete circle around the
, you make a complete circle around the
 -axis and return to the same point. Then the eigenfunction
(4.20) must again be the same, but that is only the case if
-axis and return to the same point. Then the eigenfunction
(4.20) must again be the same, but that is only the case if
 is an integer. To verify this, use the Euler formula
(2.5).
is an integer. To verify this, use the Euler formula
(2.5).
Note further that the orbital momentum is associated with a particle
whose mass is also indicated by  . This book will more
specifically indicate the magnetic quantum number as
. This book will more
specifically indicate the magnetic quantum number as  if
confusion between the two is likely.
if
confusion between the two is likely.
The above solution is easily verified directly, and the eigenvalue 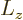 identified, by substitution into the eigenvalue
problem
identified, by substitution into the eigenvalue
problem 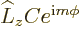

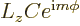 using the
expression for
using the
expression for  above:
above:
It follows that every eigenvalue is of the form:
 |
(4.21) |
So the angular momentum in a given direction cannot just take on any
value: it must be a whole multiple  , (possibly negative),
of Planck's constant
, (possibly negative),
of Planck's constant  .
.
Compare that with the linear momentum component  which can take
on any value, within the accuracy that the uncertainty principle
allows.
which can take
on any value, within the accuracy that the uncertainty principle
allows. 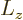 can only take discrete values, but they will be
precise. And since the
can only take discrete values, but they will be
precise. And since the  -axis was arbitrary, this is true in any
direction you choose.
-axis was arbitrary, this is true in any
direction you choose.
It is important to keep in mind that if the surroundings of the
particle has no preferred direction, the angular momentum in the
arbitrarily chosen  -direction is physically irrelevant. For
example, for the motion of the electron in an isolated hydrogen atom,
no preferred direction of space can be identified. Therefore, the
energy of the electron will only depend on its total angular momentum,
not on the angular momentum in whatever is completely arbitrarily
chosen to be the
-direction is physically irrelevant. For
example, for the motion of the electron in an isolated hydrogen atom,
no preferred direction of space can be identified. Therefore, the
energy of the electron will only depend on its total angular momentum,
not on the angular momentum in whatever is completely arbitrarily
chosen to be the  -direction. In terms of quantum mechanics, that
means that the value of
-direction. In terms of quantum mechanics, that
means that the value of  does not affect the energy. (Actually,
this is not exactly true, although it is true to very high accuracy.
The electron and nucleus have magnetic fields that give them inherent
directionality. It remains true that the
does not affect the energy. (Actually,
this is not exactly true, although it is true to very high accuracy.
The electron and nucleus have magnetic fields that give them inherent
directionality. It remains true that the  -component of net angular
momentum of the complete atom is not relevant. However, the space in
which the electron moves has a preferred direction due to the magnetic
field of the nucleus and vice-versa. It affects energy very slightly.
Therefore the electron and nucleus must coordinate their angular
momentum components, addendum {A.39}.)
-component of net angular
momentum of the complete atom is not relevant. However, the space in
which the electron moves has a preferred direction due to the magnetic
field of the nucleus and vice-versa. It affects energy very slightly.
Therefore the electron and nucleus must coordinate their angular
momentum components, addendum {A.39}.)
Key Points

- Even if the physics that you want to describe has no preferred
direction, you usually need to select some arbitrary
 -axis
to do the mathematics of quantum mechanics.
-axis
to do the mathematics of quantum mechanics.

- Spherical coordinates based on the chosen
 -axis are needed in
this and subsequent analysis. They are defined in figure
4.7.
-axis are needed in
this and subsequent analysis. They are defined in figure
4.7.

- The operator for the
 -component of angular momentum is
(4.19), where
-component of angular momentum is
(4.19), where  is the angle around the
is the angle around the  -axis.
-axis.

- The eigenvalues, or measurable values, of angular momentum in
any arbitrary direction are whole multiples
 , possibly
negative, of
, possibly
negative, of  .
.

- The whole multiple
 is called the magnetic quantum number.
is called the magnetic quantum number.
4.2.2 Review Questions
-
1.
-
If the angular momentum in a given direction is a multiple of 
 1.054 57 10
1.054 57 10 J s, then
J s, then  should have units of angular momentum. Verify that.
should have units of angular momentum. Verify that.
Solution angub-a
-
2.
-
What is the magnetic quantum number of a macroscopic, 1 kg, particle that is encircling the  -axis at a distance of 1 m at a speed of 1 m/s? Write out as an integer, and show digits you are not sure about as a question mark.
-axis at a distance of 1 m at a speed of 1 m/s? Write out as an integer, and show digits you are not sure about as a question mark.
Solution angub-b
-
3.
-
Actually, based on the derived eigenfunction,  , would any macroscopic particle ever be at a single magnetic quantum number in the first place? In particular, what can you say about where the particle can be found in an eigenstate?
, would any macroscopic particle ever be at a single magnetic quantum number in the first place? In particular, what can you say about where the particle can be found in an eigenstate?
Solution angub-c
4.2.3 Square angular momentum
Besides the angular momentum in an arbitrary direction, the other
quantity of primary importance is the magnitude of the angular
momentum. This is the length of the angular momentum vector,
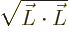 . The square root is awkward,
though; it is easier to work with the square angular momentum:
. The square root is awkward,
though; it is easier to work with the square angular momentum:
This subsection discusses the 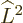 operator and its eigenvalues.
operator and its eigenvalues.
Like the  operator of the previous subsection,
operator of the previous subsection, 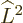 can be
written in terms of spherical coordinates. To do so, note first that
can be
written in terms of spherical coordinates. To do so, note first that
(That is the basic vector identity (D.2) with vectors
 ,
,  , and
, and 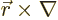 .) Next look
up the gradient and the curl in [41, pp. 124-126]. The
result is:
.) Next look
up the gradient and the curl in [41, pp. 124-126]. The
result is:
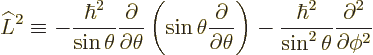 |
(4.22) |
Obviously, this result is not as intuitive as the  operator of
the previous subsection, but once again, it only involves the
spherical coordinate angles. The measurable values of square
angular momentum will be the eigenvalues of this operator. However,
that eigenvalue problem is not easy to solve. In fact the solution is
not even unique.
operator of
the previous subsection, but once again, it only involves the
spherical coordinate angles. The measurable values of square
angular momentum will be the eigenvalues of this operator. However,
that eigenvalue problem is not easy to solve. In fact the solution is
not even unique.
Table 4.2:
The first few spherical harmonics.
![\begin{table}\begin{displaymath}
\renewedcommand{arraystretch}{2.8}
\begin{arr...
...-2{\rm i}\phi}
\\ [5pt]\hline\hline
\end{array} \end{displaymath}
\end{table}](img616.gif) |
The solution to the problem may be summarized as follows. First, the
nonuniqueness is removed by demanding that the eigenfunctions are
also eigenfunctions of  , the operator of angular
momentum in the
, the operator of angular
momentum in the  -direction. This makes the problem solvable,
{D.14}, and the resulting eigenfunctions are called
the
-direction. This makes the problem solvable,
{D.14}, and the resulting eigenfunctions are called
the spherical harmonics
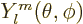 .
The first few are given explicitly in table 4.2. In case you
need more of them for some reason, there is a generic expression
(D.5) in derivation {D.14}.
.
The first few are given explicitly in table 4.2. In case you
need more of them for some reason, there is a generic expression
(D.5) in derivation {D.14}.
These eigenfunctions can additionally be multiplied by any arbitrary
function of the distance from the origin  . They are
normalized to be orthonormal integrated over the surface of the unit
sphere:
. They are
normalized to be orthonormal integrated over the surface of the unit
sphere:
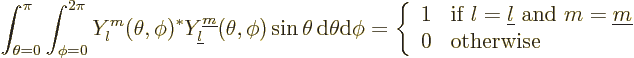 |
(4.23) |
The spherical harmonics 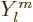 are sometimes symbolically written in
“ket notation” as
are sometimes symbolically written in
“ket notation” as 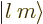 .
.
What to say about them, except that they are in general a mess? Well,
at least every one is proportional to 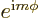 , as an
eigenfunction of
, as an
eigenfunction of  should be. More importantly, the very first
one,
should be. More importantly, the very first
one, 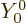 is independent of angular position compared to the origin
(it is the same for all
is independent of angular position compared to the origin
(it is the same for all  and
and  angular positions.) This
eigenfunction corresponds to the state in which there is no angular
momentum around the origin at all. If a particle has no angular
momentum around the origin, it can be found at all angular locations
relative to it with equal probability.
angular positions.) This
eigenfunction corresponds to the state in which there is no angular
momentum around the origin at all. If a particle has no angular
momentum around the origin, it can be found at all angular locations
relative to it with equal probability.
Table 4.3:
The first few spherical harmonics rewritten.
![\begin{table}\begin{displaymath}
\renewedcommand{arraystretch}{2.8}
\begin{arr...
...x- {\rm i}y)^2
\\ [5pt]\hline\hline
\end{array} \end{displaymath}
\end{table}](img623.gif) |
There is a different way of looking at the angular momentum
eigenfunctions. It is shown in table 4.3. It shows that
 is always a polynomial in the position component of degree
is always a polynomial in the position component of degree
 . Furthermore, you can check that
. Furthermore, you can check that 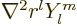
 0: the Laplacian of
0: the Laplacian of  is always zero. This way of looking at
the spherical harmonics is often very helpful in understanding more
advanced quantum topics. These solutions may be indicated as
is always zero. This way of looking at
the spherical harmonics is often very helpful in understanding more
advanced quantum topics. These solutions may be indicated as
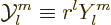 |
(4.24) |
and referred to as the “harmonic polynomials.” In general the term
harmonic
indicates a function whose Laplacian
 is zero.
is zero.
Far more important than the details of the eigenfunctions themselves
are the eigenvalues that come rolling out of the analysis. A
spherical harmonic 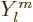 has an angular momentum in the
has an angular momentum in the
 -direction
-direction
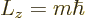 |
(4.25) |
where the integer  is called the magnetic quantum number, as noted
in the previous subsection. That is no surprise, because the analysis
demanded that they take that form. The new result is that a spherical
harmonic has a square angular momentum
is called the magnetic quantum number, as noted
in the previous subsection. That is no surprise, because the analysis
demanded that they take that form. The new result is that a spherical
harmonic has a square angular momentum
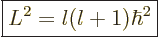 |
(4.26) |
where  is also an integer, and is called the “azimuthal quantum number” for reasons you do not want to know.
It is maybe a weird result, (why not simply
is also an integer, and is called the “azimuthal quantum number” for reasons you do not want to know.
It is maybe a weird result, (why not simply 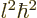 ?) but
that is what square angular momentum turns out to be.
?) but
that is what square angular momentum turns out to be.
The azimuthal quantum number is at least as large as the magnitude of
the magnetic quantum number  :
:
 |
(4.27) |
The reason is that 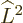

 must be at
least as large as
must be at
least as large as  ; in terms of eigenvalues,
; in terms of eigenvalues,
 must be at least as large as
must be at least as large as 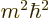 . As
it is, with
. As
it is, with 
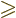
 , either the angular momentum is
completely zero, for
, either the angular momentum is
completely zero, for 


 0, or
0, or  is always greater
than
is always greater
than  .
.
Key Points

- The operator for square angular momentum is (4.22).

- The eigenfunctions of both square angular momentum and angular
momentum in the chosen
 -direction are called the spherical
harmonics
-direction are called the spherical
harmonics 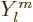 .
.

- If a particle has no angular momentum around the origin, it can
be found at all angular locations relative to it with equal
probability.

- The eigenvalues for square angular momentum take the
counter-intuitive form


 where
where  is a nonnegative integer, one of 0, 1, 2, 3, ..., and is called
the azimuthal quantum number.
is a nonnegative integer, one of 0, 1, 2, 3, ..., and is called
the azimuthal quantum number.

- The azimuthal quantum number
 is always at least as big as
the absolute value of the magnetic quantum number
is always at least as big as
the absolute value of the magnetic quantum number  .
.
4.2.3 Review Questions
-
1.
-
The general wave function of a state with azimuthal quantum number  and magnetic quantum number
and magnetic quantum number  is
is 

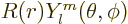 , where
, where 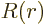 is some further arbitrary function of
is some further arbitrary function of  . Show that the condition for this wave function to be normalized, so that the total probability of finding the particle integrated over all possible positions is one, is that
. Show that the condition for this wave function to be normalized, so that the total probability of finding the particle integrated over all possible positions is one, is that
Solution anguc-a
-
2.
-
Can you invert the statement about zero angular momentum and say: if a particle can be found at all angular positions compared to the origin with equal probability, it will have zero angular momentum?
Solution anguc-b
-
3.
-
What is the minimum amount that the total square angular momentum is larger than just the square angular momentum in the  -direction for a given value of
-direction for a given value of  ?
?
Solution anguc-c
4.2.4 Angular momentum uncertainty
Rephrasing the final results of the previous subsection, if there is
nonzero angular momentum, the angular momentum in the  -direction is
always less than the total angular momentum. There is something funny
going on here. The
-direction is
always less than the total angular momentum. There is something funny
going on here. The  -direction can be chosen arbitrarily, and if you
choose it in the same direction as the angular momentum vector, then
the
-direction can be chosen arbitrarily, and if you
choose it in the same direction as the angular momentum vector, then
the  -component should be the entire vector. So, how can it always
be less?
-component should be the entire vector. So, how can it always
be less?
The answer of quantum mechanics is that the looked-for angular
momentum vector does not exist. No axis, however arbitrarily chosen, can align
with a nonexisting vector.
There is an uncertainty principle here, similar to the one of
Heisenberg for position and linear momentum. For angular momentum, it
turns out that if the component of angular momentum in a given
direction, here taken to be  , has a definite value, then the
components in both the
, has a definite value, then the
components in both the  and
and  directions will be uncertain.
(Details will be given in chapter 12.2). The wave
function will be in a state where
directions will be uncertain.
(Details will be given in chapter 12.2). The wave
function will be in a state where  and
and 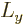 have a range of
possible values
have a range of
possible values 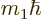 ,
, 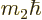 , ..., each with
some probability. Without definite
, ..., each with
some probability. Without definite  and
and  components, there
simply is no angular momentum vector.
components, there
simply is no angular momentum vector.
It is tempting to think of quantities that have not been measured,
such as the angular momentum vector in this example, as being merely
“hidden.” However, the impossibility for the  -axis to ever
align with any angular momentum vector shows that there is a
fundamental difference between
-axis to ever
align with any angular momentum vector shows that there is a
fundamental difference between being hidden
and
not existing
.
Key Points

- According to quantum mechanics, an exact nonzero angular
momentum vector will never exist. If one component of angular
momentum has a definite value, then the other two components
will be uncertain.
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]() -
-![]() -
-![]() -
-![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,![]() ,
,![]()
![]()
![]() -
-![]()
![]() -
-![]() -
-![]() -
-![]() -
-![]() -
-![]() -
-![]() -
-![]()
![]()
![]()
![]()
![]()
![]() -
-![]()
![]()
![]()
![]()
![]()
![]() -
-![]()
![]() .
.![]() .
.![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]() -
-![]() -
-![]() -
-![]()
![]() -
--
-
-
-
,
.
![]()
![]()
![]()
![]()
![]() -
-![]() ,
,![]() .
.![]()
![]()
![]() ,
,![]() -
-![]() .
.![]() .
.![]() ,
,![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]() -
-![]() :
:-
.
.
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]() .
.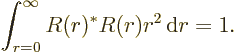
![]() -
-![]() ?
?![]() -
-![]() -
-![]() -
-![]() ,
,![]()
![]()
![]()
![]()
![]() ,
,![]() ,
,![]()
![]()
![]() -
-