| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
N.26 Physics of the fundamental commutators
The fundamental commutation relations look much like a mathematical
axiom. Surely, there should be some other reasons for physicists to
believe that they apply to nature, beyond that they seem to produce
the right answers?
Addendum {A.19} explained that the angular momentum
operators correspond to small rotations of the axis system through
space. So, the commutator ![$[{\widehat J}_x,{\widehat J}_y]$](img2680.gif) really corresponds to the
difference between a small rotation around the
really corresponds to the
difference between a small rotation around the  -axis followed
by a small rotation around the
-axis followed
by a small rotation around the  -axis, versus a small rotation
around the
-axis, versus a small rotation
around the  -axis followed by a small rotation around the
-axis followed by a small rotation around the  axis. As shown below, in our normal world this difference is
equivalent to the effect of a small rotation about the
axis. As shown below, in our normal world this difference is
equivalent to the effect of a small rotation about the  -axis.
-axis.
So, the fundamental commutator relations do have physical meaning;
they say that this basic relationship between rotations around
different axes continues to apply in the presence of spin.
This idea can be written out more precisely by using the symbols
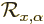 ,
,  , and
, and 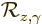 for,
respectively, a rotation around the
for,
respectively, a rotation around the  -axis over an angle
-axis over an angle
 , around the
, around the  -axis over an angle
-axis over an angle 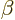 ,
and the
,
and the  -axis over an angle
-axis over an angle  . Then following
{A.19}, the angular momentum around the
. Then following
{A.19}, the angular momentum around the
 -axis is by definition:
-axis is by definition:
(To get this true exactly, you have to take the limit
 . But to keep things more physical, taking the
mathematical limit will be delayed to the end. The above expression
can be made arbitrarily accurate by just taking
. But to keep things more physical, taking the
mathematical limit will be delayed to the end. The above expression
can be made arbitrarily accurate by just taking  small
enough.)
small
enough.)
Of course, the  and
and  components of angular momentum can be
written similarly. So their commutator can be written as:
components of angular momentum can be
written similarly. So their commutator can be written as:
or multiplying out
The final expression is what was referred to above. Suppose you do a
rotation of your axis system around the  -axis over a small angle
-axis over a small angle
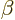 followed by a rotation around the
followed by a rotation around the  -axis around a small
angle
-axis around a small
angle  . Then you will change the position coordinates
of every point slightly. And so you will if you do the same two
rotations in the opposite order. Now if you look at the difference
between these two results, it is described by the numerator in the
final ratio above.
. Then you will change the position coordinates
of every point slightly. And so you will if you do the same two
rotations in the opposite order. Now if you look at the difference
between these two results, it is described by the numerator in the
final ratio above.
All those small rotations are of course a complicated business. It
turns out that in our normal world you can get the same differences in
position in a much simpler way: simply rotate the axis system around a
small angle 

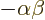 around the
around the  -axis. The
change produced by that is the numerator in the expression for the
angular momentum in the
-axis. The
change produced by that is the numerator in the expression for the
angular momentum in the  -direction given above. If the two
numerators are the same for small
-direction given above. If the two
numerators are the same for small  and
and 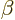 , then the
fundamental commutation relation follows. At least in our normal
world. So if physicists extend the fundamental commutation relations
to spin, they are merely generalizing a normal property of rotations.
, then the
fundamental commutation relation follows. At least in our normal
world. So if physicists extend the fundamental commutation relations
to spin, they are merely generalizing a normal property of rotations.
To show that the two numerators are the indeed the same for small
angles requires a little linear algebra. You may want to take the
remainder of this section for granted if you never had a course in it.
First, in linear algebra, the effects of rotations on position
coordinates are described by matrices. In particular,
By multiplying out, the commutator is found as
Similarly, the angular momentum around the  -axis is
-axis is
If you take the limit that the angles become zero in both expressions,
using either l’Hôpital or Taylor series expansions, you get the
fundamental commutation relationship.
And of course, it does not make a difference which of your three axes
you take to be the  -axis. So you get a total of three of these
relationships.
-axis. So you get a total of three of these
relationships.
![]()
![]() -
-![]() -
-![]() -
-![]()
![]() -
-![]() ,
,![]() ,
,![]()
![]() -
-![]() ,
,![]() -
-![]() ,
,![]() -
-![]() .
.![]() -
-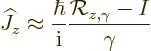
![]()
![]()
![\begin{displaymath}[{\widehat J}_x,{\widehat J}_y]\equiv {\widehat J}_x {\wideha...
...\beta}-I}{\beta} \frac{{\cal R}_{x,\alpha}-I}{\alpha}
\right)
\end{displaymath}](img7867.gif)
![\begin{displaymath}[{\widehat J}_x,{\widehat J}_y]\approx \frac{\hbar^2}{{\rm i}...
...,\beta} - {\cal R}_{y,\beta} {\cal R}_{x,\alpha}}{\alpha\beta}
\end{displaymath}](img7868.gif)
![]() -
-![]()
![]() -
-![]() .
.![]()
![]()
![]()
![]() -
-![]() -
-![]()
![]() ,
,
![\begin{displaymath}[{\widehat J}_x,{\widehat J}_y]\approx
\frac{\hbar^2}{{\rm i...
...\alpha) & -\sin\alpha(1-\cos\beta) & 0 \\
\end{array}\right)
\end{displaymath}](img7871.gif)

![]() -
-