| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
N.27 Magnitude of components of vectors
You might wonder whether the fact that the square components of
angular momentum must be less than total square angular momentum still
applies in the quantum case. After all, those components do not exist
at the same time. But it does not make a difference: just evaluate
them using expectation values. Since states 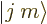 are
eigenstates, the expectation value of total square angular momentum is
the actual value, and so is the square angular momentum in the
are
eigenstates, the expectation value of total square angular momentum is
the actual value, and so is the square angular momentum in the
 -direction. And while the
-direction. And while the 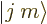 states are not eigenstates of
states are not eigenstates of
 and
and 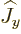 , the expectation values of square Hermitian
operators such as
, the expectation values of square Hermitian
operators such as  and
and  is always positive anyway (as
can be seen from writing it out in terms of the eigenstates of them.)
is always positive anyway (as
can be seen from writing it out in terms of the eigenstates of them.)
![]()
![]() -
-![]()
![]()
![]() ,
,![]()
![]()