| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
A.10 Spin inner product
In quantum mechanics, the angle between two angular momentum vectors
is not really defined. That is because at least two components of a
nonzero angular momentum vector are uncertain. However, the inner
product of angular momentum vectors can be well defined. In some
sense, that gives an angle between the two vectors.
An important case is the inner product between the spins of two
particles. It is related to the square net combined spin of the
particles as
If you multiply out the right hand side and rearrange, you find the
inner product between the spins as
 |
(A.29) |
Now an elementary particle has a definite square spin angular momentum
where  is the spin quantum number. If the square combined spin
also has a definite value, then so does the dot product between the
spins as given above.
is the spin quantum number. If the square combined spin
also has a definite value, then so does the dot product between the
spins as given above.
As an important example, consider two fermions with spin 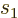

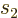

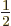 . These fermions may be in a singlet state
with combined spin
. These fermions may be in a singlet state
with combined spin 
 0. Or they may be in a
triplet state with combined spin
0. Or they may be in a
triplet state with combined spin 
 1. If that is
plugged into the formulae above, the inner product between the spins
is found to be
1. If that is
plugged into the formulae above, the inner product between the spins
is found to be
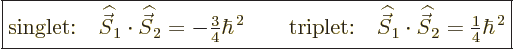 |
(A.30) |
Based on that, you could argue that in the singlet state the angle
between the spin vectors is 180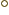 . In the triplet state
the angle is not zero, but about 70
. In the triplet state
the angle is not zero, but about 70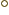 .
.

![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]() .
.![]() .
.