|
|
|
|
|
Next: A.12 Heisenberg picture |
|
This note gives additional information on thermoelectric effects.
The approximate expressions for the semiconductor Peltier coefficients
come from [29]. Straub et al (App. Phys. Let. 95,
052107, 2009) note that to better approximation, ![]()
![]()
![]()
![]() .
.
The estimate for the Peltier coefficient of a metal assumes that the
electrons form a free-electron gas. The conduction will be assumed to
be in the ![]() -
-![]()
![]() .
.![]()
![]() -
-![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
In this notation, the average charge and energy flows per electron
become
To get the heat flow, the energy must be taken relative to the Fermi
level ![]() .
.![]()
![]() .
.
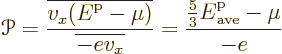
To get Seebeck coefficient ballparks, simply divide the Peltier
coefficients by the absolute temperature. That works because of
Kelvin’s second relationship discussed below. To get the Seebeck
coefficient ballpark for a metal directly from the Seebeck effect,
equate the increase in electrostatic potential energy of an electron
migrating from hot to cold to the decrease in average electron kinetic
energy. Using the average kinetic energy of derivation
{D.62}:

To compare thermoelectric materials, an important quantity is the
figure of merit of the material. The figure of merit is by convention
written as ![]()
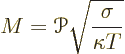
nondimensional,it has no units. In SI units, the Peltier coefficient
To see why that is relevant, suppose you have a material with a low Peltier coefficient. You might consider compensating for that by, say, scaling up the size of the material or the current through it. And maybe that does give you a better device than you would get with a material with a higher Peltier coefficient. Maybe not. How do you know?
dimensional analysis can help answer that question. It says that
nondimensional quantities depend only on nondimensional quantities.
For example, for a Peltier cooler you might define an efficiency as
the heat removed from your ice cubes per unit electrical energy used.
That is a nondimensional number. It will not depend on, say, the
actual size of the semiconductor blocks, but it will depend on such
nondimensional parameters as their shape, and their size relative to
the overall device. Those are within your complete control during the
design of the cooler. But the efficiency will also depend on the
nondimensional figure of merit ![]()
To be sure, it is somewhat more complicated than that because two
different materials are involved. That makes the efficiency depend on
at least two nondimensional figures of merit, one for each material.
And it might also depend on other nondimensional numbers that can be
formed from the properties of the materials. For example, the
efficiency of a simple thermoelectric generator turns out to depend on
a net figure of merit given by, [9],
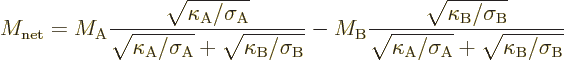
The given qualitative description of the Seebeck mechanism is very crude. For example, for semiconductors it ignores variations in the number of charge carriers. Even for a free-electron gas model for metals, there may be variations in charge carrier density that offset velocity effects. Worse, for metals it ignores the exclusion principle that restricts the motion of the electrons. And it ignores that the hotter side does not just have electrons with higher energy relative to the Fermi level than the colder side, it also has electrons with lower energy that can be excited to move. If the lower energy electrons have a larger mean free path, they can come from larger distances than the higher energy ones. And for metal electrons in a lattice, the velocity might easily go down with energy instead of up. That is readily appreciated from the spectra in chapter 6.22.2.
For a much more detailed description, see “Thermoelectric Effects in Metals: Thermocouples” by S. O. Kasap, 2001. This paper is available on the web for personal study. It includes actual data for metals compared to the simple theory.
To understand the Peltier, Seebeck, and Thomson effects more precisely, the full equations of heat and charge flow are needed. That is classical thermodynamics, not quantum mechanics. However, standard undergraduate thermodynamics classes do not cover it, and even the thick standard undergraduate text books do not provide much more than a superficial mention that thermoelectric effects exist. Therefore this subsection will describe the equations of thermoelectrics in a nutshell.
The discussion will be one-dimensional. Think of a bar of material
aligned in the ![]() -
-![]()
Heat flow is primarily driven by variations in temperature, and electric current by variations in the chemical potential of the electrons. The question is first of all what is the precise relation between those variations and the heat flow and current that they cause.
Now the microscopic scales that govern the motion of atoms and
electrons are normally extremely small. Therefore an atom or electron
sees
only a very small portion of the macroscopic
temperature and chemical potential distributions. The atoms and
electrons do notice that the distributions are not constant, otherwise
they would not conduct heat or current at all. But they see so little
of the distributions that to them they appear to vary linearly with
position. As a result it is simple gradients, i.e. first derivatives,
of the temperature and potential distributions that drive heat flow
and current in common solids. Symbolically:

heat flux density;“flux” is a fancy word for
flowand the qualifier
densityindicates that it is per unit cross-sectional area of the bar. Similarly
The above equations are not valid if the temperature and potential distributions change nontrivially on microscopic scales. For example, shock waves in supersonic flows of gases are extremely thin; therefore you cannot use equations of the type above for them. Another example is highly rarefied flows, in which the molecules move long distances without collisions. Such extreme cases can really only be analyzed numerically and they will be ignored here. It is also assumed that the materials maintain their internal integrity under the conduction processes.
Under normal conditions, a further approximation can be made. The
functions ![]()
![]()
![]()
![]()
By convention, the four coefficients are rewritten in terms of four
other, more intuitive, ones:
If conditions are isothermal, the second equation is Ohm’s law for
a unit cube of material, with ![]()
 |
(A.33) |
It is often convenient to express the heat flux density ![]()
![]() .
.
The total energy flowing through the bar is the sum of the thermal
heat flux and the energy carried along by the electrons:
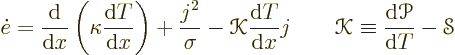
The equations (A.31) are often said to be representative of nonequilibrium thermodynamics. However, they correspond to a vanishingly small perturbation from thermodynamical equilibrium. The equations would more correctly be called quasi-equilibrium thermodynamics. Nonequilibrium thermodynamics is what you have inside a shock wave.
The statement that the charge density is neutral inside the material comes from [[8]].
A simplified macroscopic derivation can be given based on the thermoelectric equations (A.31). The derivation assumes that the temperature and chemical potential are almost constant. That means that derivatives of thermodynamic quantities and electric potential are small. That makes the heat flux and current also small.
Next, in three dimensions replace the ![]()
![]() .
.
Therefore, taking the divergence of the equations (A.31) and ignoring the variations of the coefficients, which give again quadratically small contributions, it follows that the Laplacians of both the temperature and the chemical potential are zero.
Now the chemical potential includes both the intrinsic chemical potential and the additional electrostatic potential. The intrinsic chemical potential depends on temperature. Using again the assumption that quadratically small terms can be ignored, the Laplacian of the intrinsic potential is proportional to the Laplacian of the temperature and therefore zero.
Then the Laplacian of the electrostatic potential must be zero too, to make the Laplacian of the total potential zero. And that then implies the absence of net charge inside the material according to Maxwell’s first equation, chapter 13.2. Any net charge must accumulate at the surfaces.
This subsection gives an explanation of the definition of the thermal
heat flux in thermoelectrics. It also explains that the Kelvin (or
Thomson) relationships are a special case of the more general
Onsager reciprocal relations.
If you do not know what
thermodynamical entropy is, you should not be reading this subsection.
Not before reading chapter 11, at least.
For simplicity, the discussion will again assume one-dimensional
conduction of heat and current. The physical picture is therefore
conduction along a bar aligned in the ![]() -
-
The primary question is what is going on in a single short segment
![]()
![]()
reservoirs
1 and 2 of the same material,
as shown in figure A.1. The idealized reservoirs are
assumed to remain at uniform, thermodynamically reversible,
conditions. Reservoir 1 is at the considered time at the same
temperature and chemical potential as the start of the segment, and
reservoir 2 at the same temperature and chemical potential as the end
of the segment. The reservoirs are assumed to be big enough that
their properties change slowly in time. Therefore it is assumed that
their time variations do not have an effect on what happens inside the
bar segment at the considered time. For simplicity, it will also be
assumed that the material consists of a single particle type. Some of
these particles are allowed to move through the bar segment from
reservoir 1 to reservoir 2.
In other words, there is a flow, or flux, of particles through the bar
segment. The corresponding particle flux density ![]()
![]()
![]()
![]()
Further, due to the energy carried along by the moving particles, as
well as due to thermal heat flow, there will be a net energy flow
![]()
One question is how to define the heat flux through the bar segment.
In the absence of particle motion, the second law of thermodynamics
allows an unambiguous answer. The heat flux ![]()
To understand the relationship between heat flux and energy flux more
clearly, some basic thermodynamics can be used. See chapter
11.12 for more details, including generalization to more
than one particle type. A combination of the first and second laws of
thermodynamics produces
(Chapter 11.13 does not include an additional electrostatic energy due to an ambient electric field. But an intrinsic chemical potential can be defined by subtracting the electrostatic potential energy. The corresponding intrinsic energy also excludes the electrostatic potential energy. That makes the expression for the chemical potential the same in terms of intrinsic quantities as in terms of nonintrinsic ones. See also the discussion in chapter 6.14.)
Using the above expression for the change in entropy in the definition
of the heat flux gives, noting that the volume is constant,
The Kelvin relationships are related to the net entropy generated by the segment of the bar. The second law implies that irreversible processes always increase the net entropy in the universe. And by definition, the complete system figure A.1 examined here is isolated. It does not exchange work nor heat with its surroundings. Therefore, the entropy of this system must increase in time due to irreversible processes. More specifically, the net system entropy must go up due to the irreversible heat conduction and particle transport in the segment of the bar. The reservoirs are taken to be thermodynamically reversible; they do not create entropy out of nothing. But the heat conduction in the bar is irreversible; it goes from hot to cold, not the other way around, in the absence of other effects. Similarly, the particle transport goes from higher chemical potential to lower.
While the conduction processes in the bar create net entropy, the
entropy of the bar still does not change. The bar is assumed to be in
a steady state. Instead the entropy created in the bar causes a net
increase in the combined entropy of the reservoirs. Specifically,
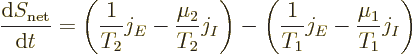
The above expression for the entropy generation implies that a nonzero
derivative of ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
The so-called Onsager reciprocal relations provide a further, and much
more specific constraint. They say that the coefficients of the
secondary effects, ![]()
![]() ,
,![]()
The Onsager relations remain valid for much more general systems,
involving flows of other quantities. Their validity can be argued
based on experimental evidence, or also theoretically based on the
symmetry of the microscopic dynamics with respect to time reversal.
If there is a magnetic field involved, a coefficient ![]()
![]()
The equations (A.36) for ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
It should be noted that while the second Kelvin relationship is named after Kelvin, he never gave a valid proof of the relationship. Neither did many other authors that tried. It was Onsager who first succeeded in giving a more or less convincing theoretical justification. Still, the most convincing support for the reciprocal relations remains the overwhelming experimental data. See Miller (Chem. Rev. 60, 15, 1960) for examples. Therefore, the reciprocal relationships are commonly seen as an additional axiom to be added to thermodynamics to allow quasi-equilibrium systems to be treated.