| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
N.8 Why the s states have the least energy
The probability of being found near the nucleus, i.e. the origin, is
determined by the magnitude of the relevant hydrogen wave function
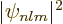 near the origin. Now the power series expansion of
near the origin. Now the power series expansion of
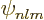 in terms of the distance
in terms of the distance  from the origin starts with
power
from the origin starts with
power 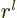 , (D.8). For small enough
, (D.8). For small enough  , a p,
(i.e.
, a p,
(i.e. 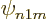 ), state involving a factor
), state involving a factor  will be much smaller
than an s, (
will be much smaller
than an s, (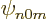 ), state without such a factor. Similarly a
d, (
), state without such a factor. Similarly a
d, (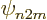 ), state involving a factor
), state involving a factor 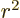 will be much less
still than a p state with just single factor
will be much less
still than a p state with just single factor  , etcetera. So
states of higher angular momentum quantum number
, etcetera. So
states of higher angular momentum quantum number  stay increasingly
strongly out of the immediate vicinity of the nucleus. This reflects
in increased energy since the nuclear attraction is much greater close
the nucleus than elsewhere in the presence of shielding.
stay increasingly
strongly out of the immediate vicinity of the nucleus. This reflects
in increased energy since the nuclear attraction is much greater close
the nucleus than elsewhere in the presence of shielding.
![]()
![]()
![]()
![]() ,
,![]() ,
,![]() )
)![]()
![]() )
)![]() )
)![]()
![]() ,
,![]()