| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
N.9 Explanation of the band gaps
Chapter 6.21 showed that the spectra of the electrons of
solids have band gaps;
energy ranges for which there
are no quantum states for the electrons. These band gaps were
qualitatively explained as the remnants of the discrete electron
energy states of the individual atoms. These discrete energy states
spread out when multiple atoms start interacting, but not necessarily
enough to completely remove the gaps.
However, if you start from the free-electron gas point of view, it is
much less clear why and when addition of just a bit of crystal potential
would suddenly pop up band gaps out of nothing. If you are curious,
this note is for you.
To understand what is going on, the Kronig & Penney model will be
used. The crystal
is again taken to be one-dimensional.
The potential consists again of a sequence of straight dips, as was
shown in green in 6.22. The dips represent the attraction
of the atoms on the individual atomic electrons. However, to allow an
easier comparison with the free-electron gas solutions, this time the
dips will taken far less deep than before. Think of it as a model for
a metal, where the outer electrons are only very weakly bound to their
atomic cores.
For these shallower atomic
dips, and for a crystal
consisting of very many atoms,
the energy levels are
as shown to the left in figure N.1. Note that for the
higher energies, this is generally speaking very similar to the energy
levels for the free-electron spectrum shown to the left. That should
be expected; why would the shallow potential energy dips have much of
an effect when the kinetic energy of the electron considered is very
large? But even for high energy levels, there are still occasional
thin gaps. At these gaps, the electron velocity plunges to zero.
Why are these gaps there?
Figure N.1:
Spectrum for a weak potential.
![\begin{figure}\centering
\setlength{\unitlength}{1pt}
\begin{picture}(400,21...
...al}}
\put(100,-2){\makebox(0,0)[b]{free electrons}}
\end{picture}
\end{figure}](img7777.gif) |
To qualitatively understand what is going on, from here on it will be
assumed that the periodic crystal
consists of just 12
atoms,
(rather than, say, a million). Mathematically,
after twelve atoms, the quantum wave function becomes the same as it
was initially and the solution repeats. You may think of the twelve
atoms as physically being arranged in a ring shape.
Figure N.2:
The 17 real
wave functions of lowest energy for a small one-dimensional periodic
box with only 12 atomic cells. Black curves show the square
wave function, which gives the relative probability of finding
the electron at that location.
![\begin{figure}\centering
\setlength{\unitlength}{1pt}
\begin{picture}(405,46...
...bwwf82.eps}}}
\put(0,450){\makebox(0,0)[b]{$z=16$}}
\end{picture}
\end{figure}](img7778.gif) |
To make things easier to understand, it is also desirable to switch
from the complex Bloch wave
wave functions to the
equivalent real ones. These real wave functions may be found as the
real and imaginary parts of the Bloch waves. That is easiest for the
free-electron gas, where the Bloch waves are simply complex
exponentials; the Euler identity says
So for the free-electron gas, the real wave functions are 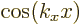 and
and 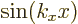 , ignoring an unimportant normalization constant. As
before, the wave number
, ignoring an unimportant normalization constant. As
before, the wave number 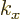 is a measure of the “crystal
momentum”
is a measure of the “crystal
momentum” 

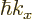 , which is turn
related to the electron velocity
, which is turn
related to the electron velocity 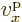 through the energy.
through the energy.
For the Kronig-Penney model, the real wave functions are more complex
than simple sines and cosines, but can be found the same way.
Note that normally there are two different wave functions for each
value of the wave number 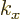 . The one exception is for the ground
state of lowest energy where
. The one exception is for the ground
state of lowest energy where 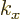 is zero. In terms of the free
electron gas,
is zero. In terms of the free
electron gas, 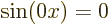 . Zero is not a valid wave function.
Remember that the square magnitude of a wave function gives the
probability of finding the electron. So if a wave function would be
zero, there would not be any chance of finding the electron anywhere.
So there would be no electron.
. Zero is not a valid wave function.
Remember that the square magnitude of a wave function gives the
probability of finding the electron. So if a wave function would be
zero, there would not be any chance of finding the electron anywhere.
So there would be no electron.
For the free-electron gas, that leaves as only ground state wave
function 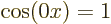 times some constant. That is just a constant.
And since the square of a constant is still a constant, that means
that the probability of finding the electron is the same everywhere in
the period.
times some constant. That is just a constant.
And since the square of a constant is still a constant, that means
that the probability of finding the electron is the same everywhere in
the period.
For the Kronig-Penney case, the situation is a less simple. Consider
first the ground state, shown in the picture at the bottom of figure
N.2. (In figure N.2 the height of a wave
function picture illustrates the relative amount of energy of that
wave function. So the ground state picture is at the bottom.) The
square magnitude of the ground state wave function, shown as the black
line, is no longer a constant. It is higher than average at the dips
in the potential, at the atoms.
It is lower than
average in between atoms.
So the electron is somewhat
more likely to be found near an atom that attracts it than in between
atoms. The electron reduces its potential energy that way. But it
cannot do this without limit; if the electron is only found at the
atoms, the reduced uncertainty in position increases the kinetic
energy more than the potential energy is lowered. The best compromise
is given by the black line at the bottom of figure N.2.
To understand the energy states above the ground state, a key concept
of the general mathematical properties of real one-dimensional wave
functions is needed: The more zero crossings in the wave
function, the higher the energy.
Qualitatively, the reason is not that hard to understand. The more
zero crossings, the more wildly the wave function swings back and
forward between positive and negative values, raising the kinetic
energy. In figure N.2 the number of zero crossings is
listed as  . Note that by squaring the wave functions, the zero
crossings become touching zero, not crossing it.
. Note that by squaring the wave functions, the zero
crossings become touching zero, not crossing it.
Note further that only even numbers of zero crossings  appear. A
periodic wave function must return to the same sign at the end of the
period as at the start, and that is only possible if the number of
zero crossings is even.
appear. A
periodic wave function must return to the same sign at the end of the
period as at the start, and that is only possible if the number of
zero crossings is even.
Note next that in almost all cases, there are two different
wave functions of the same energy at a given number of zero
crossings. That is because if you have one wave function at a given
 , you can simply shift it over by one atomic cell, and you have
another wave function of the same energy. This second wave function
is almost always a different one. In particular, it can only
be the same wave function if the
, you can simply shift it over by one atomic cell, and you have
another wave function of the same energy. This second wave function
is almost always a different one. In particular, it can only
be the same wave function if the  zeros are still in the same
place. But if you have 12 atomic cells and, say,
zeros are still in the same
place. But if you have 12 atomic cells and, say, 
 8 zeros,
then some of the 12 atomic cells must have zeros and other ones not.
So the shifted wave function cannot possibly have all its zeros in the
same place. So the shifted wave function is a second, different, wave
function of the same energy. So there are two different wave
functions with the same
8 zeros,
then some of the 12 atomic cells must have zeros and other ones not.
So the shifted wave function cannot possibly have all its zeros in the
same place. So the shifted wave function is a second, different, wave
function of the same energy. So there are two different wave
functions with the same  and energy.
and energy.
The only way this can possibly fail, and does, is if each atomic cell
has the same number of zeros as its next neighbor. So every atomic
cell must have the same number of zeros in it.
That, then, is why it is possible at all that there is only one wave
function in the ground state. In the ground state there are no zeros,
so every atomic cell has the same number, none. Indeed, looking
closer, in the ground state the wave function is identical in every
atomic cell. Mathematically, for 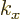
 0, the exponential part
of the Bloch wave is just a trivial constant, making the complete
Bloch wave the same for all atomic cells. So shifting the wave
function over one atomic cell gives you back the exact same thing.
0, the exponential part
of the Bloch wave is just a trivial constant, making the complete
Bloch wave the same for all atomic cells. So shifting the wave
function over one atomic cell gives you back the exact same thing.
The next possibility that the shifted wave function does not give a
different one occurs when every atomic cell has one zero crossing.
For a crystal
of 12 atomic cells, that requires that
there are 
 12 zero crossings. This happens when the
wavenumber
12 zero crossings. This happens when the
wavenumber 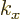

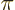

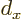 where
where 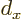 is the atomic cell
size. Then the exponential part of the Bloch wave function in any
atomic cell is identical to that in the next atomic cell except for a
mere minus sign. So the shifted wave function is only different by a
minus sign. This means it is physically equivalent to the original
one. Not a separate wave function.
is the atomic cell
size. Then the exponential part of the Bloch wave function in any
atomic cell is identical to that in the next atomic cell except for a
mere minus sign. So the shifted wave function is only different by a
minus sign. This means it is physically equivalent to the original
one. Not a separate wave function.
But even if shifting the wave function does not give you a second one,
still there must be two different eigenfunctions for each even
number of zeros  greater than zero. In particular, the wave
functions in figure N.2 were obtained in two ways. For the
wave functions in the left-hand column, it was assumed that the
derivative of the wave function is zero at the start of the period
(like it is for the
greater than zero. In particular, the wave
functions in figure N.2 were obtained in two ways. For the
wave functions in the left-hand column, it was assumed that the
derivative of the wave function is zero at the start of the period
(like it is for the 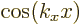 free-electron gas solutions). For
the wave functions in the right-hand column, it was assumed that the
wave function itself is zero at the start of the period (like it is
for the
free-electron gas solutions). For
the wave functions in the right-hand column, it was assumed that the
wave function itself is zero at the start of the period (like it is
for the 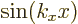 free-electron gas solutions). These are two
different solutions; they cannot be equivalent because the right-hand
wave function has a zero at the start of the period, but the left-hand
one does not.
free-electron gas solutions). These are two
different solutions; they cannot be equivalent because the right-hand
wave function has a zero at the start of the period, but the left-hand
one does not.
For one, this explains why for the ground state where 
 0,
there is no right-hand wave function. If you start out with a zero
crossing, you must have at least one of them. It also explains why a
wave function in the right column is not just the wave function in the
left column shifted by an atomic cell. The two wave functions were
separately computed. In almost all cases, the right-hand wave
function is then a combination of the shifted and unshifted
left-hand wave functions, the combination that is zero at the start of
the period. In about half the cases, that turns out to be the left
wave function shifted by a quarter period, in the other half of the
cases it is just all different. The energy of the two solutions is
still the same.
0,
there is no right-hand wave function. If you start out with a zero
crossing, you must have at least one of them. It also explains why a
wave function in the right column is not just the wave function in the
left column shifted by an atomic cell. The two wave functions were
separately computed. In almost all cases, the right-hand wave
function is then a combination of the shifted and unshifted
left-hand wave functions, the combination that is zero at the start of
the period. In about half the cases, that turns out to be the left
wave function shifted by a quarter period, in the other half of the
cases it is just all different. The energy of the two solutions is
still the same.
But for the special case of 
 12 zeros for the 12 atomic
cells, figure N.2 shows that the left and right wave
functions are physically fundamentally different. In the left-hand
wave function, the electron is most likely to be found in the region
of high potential energy between atoms. All the peaks in wave
function are there. In the right-hand wave function, the electron is
most likely to be found in the region of low potential energy at the
atoms. The peaks are there. That means that the left hand wave
function has a lot more potential energy than the right-hand one. So
the two wave functions do not have the same energy in this
case. We have a band gap when the number of zeros is exactly the same
as the number of atoms.
12 zeros for the 12 atomic
cells, figure N.2 shows that the left and right wave
functions are physically fundamentally different. In the left-hand
wave function, the electron is most likely to be found in the region
of high potential energy between atoms. All the peaks in wave
function are there. In the right-hand wave function, the electron is
most likely to be found in the region of low potential energy at the
atoms. The peaks are there. That means that the left hand wave
function has a lot more potential energy than the right-hand one. So
the two wave functions do not have the same energy in this
case. We have a band gap when the number of zeros is exactly the same
as the number of atoms.
Similarly there will be a band gap at 
 24, where there are two
zero crossings in each atomic cell, etcetera. The band gaps occur at
whole multiples of the number of atomic cells. And there are 12
energy states in each band. For a physically realistic number of
atomic cells, call it a million instead of 12, there are a million
energy states between band gaps, effectively forming a continuum band
between the gaps.
24, where there are two
zero crossings in each atomic cell, etcetera. The band gaps occur at
whole multiples of the number of atomic cells. And there are 12
energy states in each band. For a physically realistic number of
atomic cells, call it a million instead of 12, there are a million
energy states between band gaps, effectively forming a continuum band
between the gaps.
One thing that may still be counter-intuitive is why the right-hand

 12 wave function has higher, rather than much lower energy
than the
12 wave function has higher, rather than much lower energy
than the 
 10 ones. In particular, the peaks in the
right-hand wave function at
10 ones. In particular, the peaks in the
right-hand wave function at 
 12 are all perfectly aligned
with the atomic locations. That greatly reduces the potential energy.
But in the
12 are all perfectly aligned
with the atomic locations. That greatly reduces the potential energy.
But in the 
 10 case the peaks are not aligned with the atoms.
While the
10 case the peaks are not aligned with the atoms.
While the 
 10 case has some advantage in kinetic energy with
less zero crossings, that advantage is small. That would not be able
to explain it if the right-hand
10 case has some advantage in kinetic energy with
less zero crossings, that advantage is small. That would not be able
to explain it if the right-hand 
 12 would really have a big
advantage in potential energy over the
12 would really have a big
advantage in potential energy over the 
 10 states.
10 states.
To see why it is possible, look more closely at the 
 10 case
in figure N.2. It is true that a significant fraction of
the peaks in wave function are in between atoms instead of on top of
atoms. However, the physics modulates the height of the peaks
so that the big peaks are the ones on top of the atoms, and the small
peaks the ones in between atoms. That still has the effect that the
electron is most likely found at an atom, still greatly reducing the
potential energy. That eliminates the apparent advantage of the
right-hand
10 case
in figure N.2. It is true that a significant fraction of
the peaks in wave function are in between atoms instead of on top of
atoms. However, the physics modulates the height of the peaks
so that the big peaks are the ones on top of the atoms, and the small
peaks the ones in between atoms. That still has the effect that the
electron is most likely found at an atom, still greatly reducing the
potential energy. That eliminates the apparent advantage of the
right-hand 
 12 state in potential energy.
12 state in potential energy.
Also note that for 
 10, the number of zeros is still close to
the number of atoms. So the distance between peaks is still almost
the same as the distance between atoms, (especially for a million
atoms instead of 12). So if, say, a peak is pretty much on top of an
atom, the neighboring peaks are too. Therefore the modulation of peak
amplitudes can be done in a way that slowly varies along the length of
the crystal. So it does not add a big amount to the kinetic energy.
10, the number of zeros is still close to
the number of atoms. So the distance between peaks is still almost
the same as the distance between atoms, (especially for a million
atoms instead of 12). So if, say, a peak is pretty much on top of an
atom, the neighboring peaks are too. Therefore the modulation of peak
amplitudes can be done in a way that slowly varies along the length of
the crystal. So it does not add a big amount to the kinetic energy.
However, because of the modulation, the 
 10 wave functions do
give up almost all their small kinetic energy advantage compared to
the right-hand
10 wave functions do
give up almost all their small kinetic energy advantage compared to
the right-hand 
 12 case. That means that the two energies
become very close together. Since the change in energy is a measure
of the electron propagation velocity
12 case. That means that the two energies
become very close together. Since the change in energy is a measure
of the electron propagation velocity 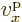 , that velocity plunges
to zero. Which is exactly what you see in figure N.1.
, that velocity plunges
to zero. Which is exactly what you see in figure N.1.
Similarly for the 
 14 wave functions, the peaks are modulated
so that the electron is most likely to be found in between atoms, just
like for the left-hand
14 wave functions, the peaks are modulated
so that the electron is most likely to be found in between atoms, just
like for the left-hand 
 12 wave function. So the
12 wave function. So the 
 14 wave functions have about the same potential energy as the
left-hand
14 wave functions have about the same potential energy as the
left-hand 
 12 one. And because the
12 one. And because the 
 12 wave
function is so effective in raising its potential energy, you would
expect that the energy difference with the
12 wave
function is so effective in raising its potential energy, you would
expect that the energy difference with the 
 14 case would be
relatively small, producing small electron velocity. And that is
indeed what happens.
14 case would be
relatively small, producing small electron velocity. And that is
indeed what happens.
So the only finite energy gaps occur when the number of zeros is a
whole multiple of the number of atoms. And the gap is between the two
states with that number of zeros.
And between the states immediately above and below the gaps, the
energy difference is even smaller than elsewhere in the band. That
makes the electron velocity 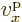 zero at the edges of the bands
zero at the edges of the bands
Since the wave functions at the edges of the bands have zero
propagation velocity, electrons in these states cannot move through
the crystal. Now an implicit result of the analysis above is that for
these states, a whole multiple of the Bloch wave length must equal
double the atomic spacing. The Bloch exponential can change sign
going from one atomic cell to the next, then return to the original
sign at the next cell, but nothing more. If you train a beam of
electrons with a wave length like that onto the crystal, the beam
cannot propagate and will be totally reflected. That is in fact a key
result of the Bragg reflection theory of wave mechanics,
(10.16) in chapter 10.7.2. Thus Bragg theory
can provide an intuitive justification for some of the features of the
band structure.
If you want to see mathematically that the propagation velocity is
indeed zero at the band gaps, and you know linear algebra, you can
find the derivation in {D.84}. That also explains
how the wave function figures in figure N.2 were made.
![\begin{figure}\centering
\setlength{\unitlength}{1pt}
\begin{picture}(405,46...
...bwwf82.eps}}}
\put(0,450){\makebox(0,0)[b]{$z=16$}}
\end{picture}
\end{figure}](img7778.gif)
![]() .
.![]()
![]() .
.![]()
![]() .
.![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()