| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
D.66 The triangle inequality
The normal triangle inequality continues to apply for expectation
values in quantum mechanics.
The way to show that is, like other triangle inequality proofs, rather
curious: examine the combination of 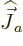 , not with
, not with
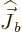 , but with an arbitrary multiple
, but with an arbitrary multiple 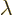 of
of
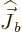 :
:
For 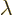
 1 this produces the expectation value of
1 this produces the expectation value of
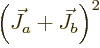 , for
, for 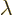

 1,
the one for
1,
the one for 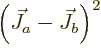 . In addition,
it is positive for all values of
. In addition,
it is positive for all values of 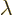 , since it consists of
expectation values of square Hermitian operators. (Just examine each
term in terms of its own eigenstates.)
, since it consists of
expectation values of square Hermitian operators. (Just examine each
term in terms of its own eigenstates.)
If you multiply out, you get
where 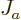

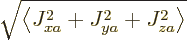 ,
,
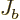

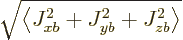 ,
and
,
and  represents mixed terms that do not need to be written out. In
order for this quadratic form in
represents mixed terms that do not need to be written out. In
order for this quadratic form in 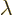 to always be positive, the
discriminant must be negative:
to always be positive, the
discriminant must be negative:
which means, taking square roots,
and so
or
and taking square roots gives the triangle inequality.
Note that this derivation does not use any properties specific to
angular momentum and does not require the simultaneous existence of
the components. With a bit of messing around, the azimuthal quantum
number relation 

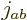

 can be
derived from it if a unique value for
can be
derived from it if a unique value for 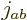 exists; the key is to
recognize that
exists; the key is to
recognize that 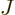

 where
where 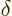 is an increasing
function of
is an increasing
function of  that stays below
that stays below  , and the
, and the  values
must be half integers. This derivation is not as elegant as using the
ladder operators, but the result is the same.
values
must be half integers. This derivation is not as elegant as using the
ladder operators, but the result is the same.
![]() ,
,![]() ,
,![]()
![]() :
: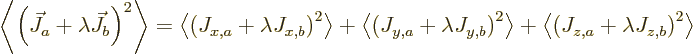
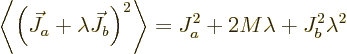
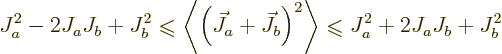
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()