| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
D.67 Momentum of shells
Table 12.1 was originally taken from
[36], who in turn took it from the book of Mayer
and Jensen. However, the final table contains three typos, as can be
seen from the fact that in three cases the numbers of states do not
add up to the correct total. (The errors are: for 3 particles with
spin 9/2, the 13/2 combined state is omitted, for 4 particles with
spin 9/2, the spin 8 state should be double, and for 4 particles with
spin 11/2, a spin 7 (double) state is missing. Similarly,
[5, p. 140] has the same missing 13/2 combined state,
and in addition for 3 particles with spin 7/2, there is a 1/2 state
that should not be there.)
So table 12.1 was instead computer-generated, and should
therefore be free of typos. Since the program had to be written
anyway, some more values were generated and are in table
D.1.
Deducing the table using Clebsch-Gordan coefficients would be a messy
exercise indeed. A simpler procedure, [31], will here be
illustrated for the example that the number of fermions is 
 3
and the angular momentum of the single-particle states is
3
and the angular momentum of the single-particle states is 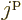

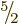 . Then the possibilities for the single-particle
angular momentum in the
. Then the possibilities for the single-particle
angular momentum in the  -direction are
-direction are 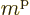

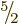 ,
,  ,
,  ,
,
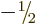 ,
, 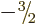 , and
, and 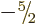 . So there
are 6 different one particle states, and these will give rise to
6!
. So there
are 6 different one particle states, and these will give rise to
6! 3!(6-3)! = 20 different antisymmetric states for 3 particles,
chapter 5.7.
3!(6-3)! = 20 different antisymmetric states for 3 particles,
chapter 5.7.
Table D.1:
Additional combined angular momentum values.
 |
The combination states can be chosen to have definite values of the
combined angular momentum  and momentum in the
and momentum in the  -direction
-direction
 . In the absence of any antisymmetrization requirements,
that can be seen from the way that states combine using Clebsch-Gordan
coefficients. And these states of definite combined angular momentum
must either be antisymmetric and allowable, or symmetric and not
allowed. The reason is that exchanging fermions does not do anything
physically, since the fermions are identical. So the angular momentum
and particle exchange operators commute. Therefore, the eigenstates
of the angular momentum operators can also be taken to be eigenstates
of the particle exchange operators, which means either symmetric
(eigenvalue 1) or antisymmetric (eigenvalue
. In the absence of any antisymmetrization requirements,
that can be seen from the way that states combine using Clebsch-Gordan
coefficients. And these states of definite combined angular momentum
must either be antisymmetric and allowable, or symmetric and not
allowed. The reason is that exchanging fermions does not do anything
physically, since the fermions are identical. So the angular momentum
and particle exchange operators commute. Therefore, the eigenstates
of the angular momentum operators can also be taken to be eigenstates
of the particle exchange operators, which means either symmetric
(eigenvalue 1) or antisymmetric (eigenvalue  1).
1).
Let  be the total magnetic quantum number of the 3 fermions in any
combination of
be the total magnetic quantum number of the 3 fermions in any
combination of 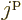

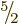 single-particle states. First
note that
single-particle states. First
note that  is the sum of the three
is the sum of the three 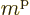 values of the individual
particles. Next, the highest that
values of the individual
particles. Next, the highest that 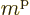 can be is
can be is 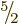 ,
but the fermions cannot all three be in the same
,
but the fermions cannot all three be in the same 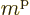

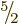 state, only one can. Three fermions need three different
states, so the highest the combined
state, only one can. Three fermions need three different
states, so the highest the combined  can be is
can be is
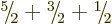 . This triplet of values of
. This triplet of values of 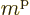 gives exactly one antisymmetric combination of states with
gives exactly one antisymmetric combination of states with 

 . (There is only one Slater determinant for three
different given states, chapter 5.7). Since the
combined angular momentum of this state in any arbitrary direction can
never be observed to be more than
. (There is only one Slater determinant for three
different given states, chapter 5.7). Since the
combined angular momentum of this state in any arbitrary direction can
never be observed to be more than  , because that would
violate the above argument in a rotated coordinate system, it must be
a
, because that would
violate the above argument in a rotated coordinate system, it must be
a 

 state. The first conclusion is therefore that
the angular momenta cannot combine into a total greater than
state. The first conclusion is therefore that
the angular momenta cannot combine into a total greater than 

 . And since
. And since  cannot be less than
cannot be less than  , there
must be states with
, there
must be states with 

 .
.
But note that if 



 is a valid combination
of single-particle states, then so should be the states with
is a valid combination
of single-particle states, then so should be the states with 

 for the other values of
for the other values of  ; these can be thought of
as fully equivalent states simply oriented under a different angle.
That means that there are a total of 10 combination states with
; these can be thought of
as fully equivalent states simply oriented under a different angle.
That means that there are a total of 10 combination states with 

 , in which
, in which  is any one of
is any one of  ,
,
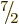 , ...,
, ...,  .
.
Next consider what combinations have 

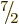 . The
only combination of three different
. The
only combination of three different 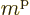 values that adds up to
values that adds up to
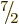 is
is 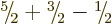 . So there is only
one combined state with
. So there is only
one combined state with 

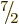 . Since it was
already inferred above that there must be one such state with
. Since it was
already inferred above that there must be one such state with 

 , that must be the only one. So apparently
there is no state with
, that must be the only one. So apparently
there is no state with 

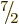 : such a state would
show up as a second
: such a state would
show up as a second 

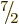 state under the right
orientation.
state under the right
orientation.
There are two independent possibilities to create a triplet of
different states with 

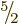 :
:
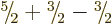 or
or 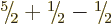 .
One combination of such a type is already identified as being a
.
One combination of such a type is already identified as being a 

 state, so the second must correspond to a
state, so the second must correspond to a 

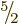 state. Since the orientation should again not make a
difference, there must be a total of 6 such states, one for each of
the different values of
state. Since the orientation should again not make a
difference, there must be a total of 6 such states, one for each of
the different values of  in the range from
in the range from 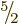 to
to
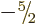 .
.
There are three ways to create a triplet of states with 

 :
: 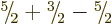 ,
,
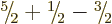 , and
, and
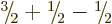 . Two of these are already
identified as being
. Two of these are already
identified as being 

 and
and 

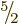 , so there must be one set of 4 states with
, so there must be one set of 4 states with 

 .
.
That makes a total of 20 states, so there must not be any states with


 . Indeed, there are only three ways to
produce
. Indeed, there are only three ways to
produce 

 :
:
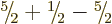 ,
,
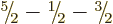 , and
, and
 , and each of these three states is
already assigned to a value of
, and each of these three states is
already assigned to a value of  .
.
It is tricky, but it works. And it is easily put on a computer.
For bosons, the idea is the same, except that states with equal values
of 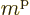 can no longer be excluded.
can no longer be excluded.
![]()
![]()
![]()
![]()
![]() .
.![]() -
-![]()
![]()
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.![]()
![]()
![]() -
-![]() .
.![]() 1
1![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]() .
.![]() ,
,![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]() ,
,![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ;
;![]()
![]()
![]() ,
,![]()
![]() ,
,![]() ,
,![]() .
.![]()
![]()
![]() .
.![]()
![]()
![]() .
.![]()
![]()
![]() .
.![]()
![]()
![]() ,
,![]()
![]()
![]() :
:![]()
![]()
![]()
![]()
![]()
![]() :
:![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]() :
:![]() ,
,![]() ,
,![]() .
.![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]() .
.![]()
![]()
![]() .
.![]()
![]()
![]() :
:![]() ,
,![]() ,
,![]() ,
,![]() .
.![]()