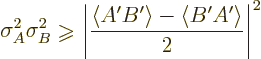| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
D.19 The generalized uncertainty relationship
This note derives the generalized uncertainty relationship.
For brevity, define 

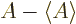 and
and 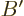

 , then the general expression for standard
deviation says
, then the general expression for standard
deviation says
Hermitian operators can be taken to the other side of inner products,
so
Now the Cauchy-Schwartz inequality says that for any  and
and
 ,
,
(See the notations for more on this theorem.) Using the
Cauchy-Schwartz inequality in reversed order, you get
Now by the definition of the inner product, the complex conjugate of
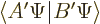 is
is  , so the complex
conjugate of
, so the complex
conjugate of  is
is 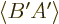 , and averaging a complex
number with minus its complex conjugate reduces its size, since the
real part averages away, so
, and averaging a complex
number with minus its complex conjugate reduces its size, since the
real part averages away, so
The quantity in the top is the expectation value of the commutator
![$[A',B']$](img6212.gif) . Writing it out shows that
. Writing it out shows that ![$[A',B']$](img6212.gif)

![$[A,B]$](img786.gif) .
.
![]()
![]()
![]()
![]()
![]()
![]() ,
,