| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
11.3 How Many System Eigenfunctions?
The fundamental question from which all of quantum statistics springs
is a very basic one: How many system energy eigenstates are there with
given generic properties? This section will address that question.
Of course, by definition each system energy eigenfunction is unique.
Figures 11.1-11.3 give examples of such
unique energy eigenfunctions for systems of distinguishable particles,
indistinguishable bosons, and indistinguishable fermions. But trying
to get accurate data on each individual eigenfunction just does not
work. That is much too big a challenge.
Quantum statistics must satisfy itself by figuring out the
probabilities on groups of system eigenfunctions with similar
properties. To do so, the single-particle energy eigenstates are best
grouped together on shelves of similar energy, as illustrated in
figures 11.1-11.3. Doing so allows for more
answerable questions such as: “How many system energy
eigenfunctions 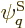 have
have  out of the
out of the  total particles on
shelf 1, another
total particles on
shelf 1, another 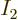 on shelf 2, etcetera?” In other words,
if
on shelf 2, etcetera?” In other words,
if 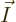 stands for a given set of shelf occupation numbers
stands for a given set of shelf occupation numbers
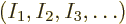 , then what is the number
, then what is the number 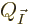 of
system eigenfunctions
of
system eigenfunctions 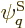 that have those shelf occupation
numbers?
that have those shelf occupation
numbers?
That question is answerable with some clever mathematics; it is a big
thing in various textbooks. However, the suspicion is that this is
more because of the neat
mathematics than because of
the actual physical insight that these derivations provide. In this
book, the derivations are shoved away into {D.56}. But
here are the results. (Drums please.) The system eigenfunction
counts for distinguishable particles, bosons, and fermions are:
where  means the product of all the terms of the form shown to
its right that can be obtained by substituting in every possible value
of the shelf number
means the product of all the terms of the form shown to
its right that can be obtained by substituting in every possible value
of the shelf number  . That is just like
. That is just like  would mean
the sum of all these terms. For example, for distinguishable
particles
would mean
the sum of all these terms. For example, for distinguishable
particles
where  is the number of single-particle energy states on shelf 1
and
is the number of single-particle energy states on shelf 1
and  the number of particles on that shelf,
the number of particles on that shelf, 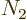 the number of
single-particle energy states on shelf 2 and
the number of
single-particle energy states on shelf 2 and 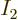 the number of
particles on that shelf, etcetera. Also an exclamation mark indicates
the factorial function, defined as
the number of
particles on that shelf, etcetera. Also an exclamation mark indicates
the factorial function, defined as
For example, 5! = 1  2
2  3
3  4
4  5 =
120. The eigenfunction counts may also involve 0!, which is defined
to be 1, and
5 =
120. The eigenfunction counts may also involve 0!, which is defined
to be 1, and  ! for negative
! for negative  , which is defined to
be infinity. The latter is essential to ensure that the eigenfunction
count is zero as it should be for fermion eigenfunctions that try to
put more particles on a shelf than there are states on it.
, which is defined to
be infinity. The latter is essential to ensure that the eigenfunction
count is zero as it should be for fermion eigenfunctions that try to
put more particles on a shelf than there are states on it.
This section is mainly concerned with explaining qualitatively why
these system eigenfunction counts matter physically. And to do
so, a very simple model system having only three shelves will suffice.
Figure 11.4:
Illustrative small model system having 4
distinguishable particles. The particular eigenfunction shown
is arbitrary.
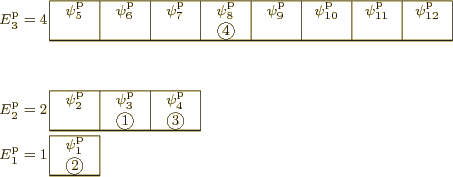 |
The first example is illustrated in quantum-mechanical terms in figure
11.4. Like the other examples, it has only three
shelves, and it has only 
 4 distinguishable particles. Shelf 1
has
4 distinguishable particles. Shelf 1
has 
 1 single-particle state with energy
1 single-particle state with energy 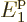
 1
(arbitrary units), shelf 2 has
1
(arbitrary units), shelf 2 has 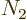
 3 single-particle states with
energy
3 single-particle states with
energy 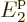
 2, (note that 3
2, (note that 3 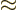
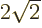 ), and shelf
3 has
), and shelf
3 has 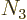

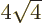
 8 single-particle states with energy
8 single-particle states with energy
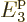
 4. One major deficiency of this model is the small number of
particles and states, but that will be fixed in the later examples.
More seriously is that there are no shelves with energies above
4. One major deficiency of this model is the small number of
particles and states, but that will be fixed in the later examples.
More seriously is that there are no shelves with energies above
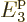
 4. To mitigate that problem, for the time being the average
energy per particle of the system eigenfunctions will be restricted to
no more than 2.5. This will leave shelf 3 largely empty, reducing the
effects of the missing shelves of still higher energy.
4. To mitigate that problem, for the time being the average
energy per particle of the system eigenfunctions will be restricted to
no more than 2.5. This will leave shelf 3 largely empty, reducing the
effects of the missing shelves of still higher energy.
Figure 11.5:
The number of system energy eigenfunctions for a simple
model system with only three energy shelves. Positions of the
squares indicate the numbers of particles on shelves 2 and 3;
darkness of the squares indicates the relative number of
eigenfunctions with those shelf numbers. Left: system with 4
distinguishable particles, middle: 16, right: 64.
![\begin{figure}\centering
{}%
\setlength{\unitlength}{1pt}
\begin{picture}(4...
...]{$I_3/I$}}
\put(278,68){\makebox(0,0)[l]{$I_3/I$}}
\end{picture}
\end{figure}](img2329.gif) |
Now the question is, how many energy eigenfunctions are there for a
given set of shelf occupation numbers 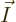

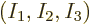 ? The answer, as given by (11.1), is
shown graphically in the left graph of figure 11.5. Darker
squares indicate more eigenfunctions with those shelf occupation
numbers. The oblique line in figure 11.5 is the line above
which the average energy per particle exceeds the chosen limit of 2.5.
? The answer, as given by (11.1), is
shown graphically in the left graph of figure 11.5. Darker
squares indicate more eigenfunctions with those shelf occupation
numbers. The oblique line in figure 11.5 is the line above
which the average energy per particle exceeds the chosen limit of 2.5.
Some example observations about the figure may help to understand it.
For example, there is only one system eigenfunction with all 4
particles on shelf 1, i.e. with 
 4 and
4 and 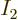

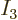
 0; it is
0; it is
This is represented by the white square at the origin in the left
graph of figure 11.5.
As another example, the darkest square in the left graph of figure
11.5 represents system eigenfunctions that have shelf
numbers 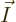

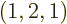 , i.e.
, i.e. 
 1,
1, 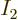
 2,
2, 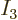
 1: one particle on shelf 1, two particles on
shelf 2, and one particle on shelf 3. A completely arbitrary example
of such a system energy eigenfunction,
1: one particle on shelf 1, two particles on
shelf 2, and one particle on shelf 3. A completely arbitrary example
of such a system energy eigenfunction,
is the one depicted in figure 11.4. It has particle
1 in single-particle state  , which is on shelf 2,
particle 2 in
, which is on shelf 2,
particle 2 in 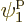 , which is on shelf 1, particle 3 in
, which is on shelf 1, particle 3 in
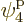 which is on shelf 2, and particle 4 in
which is on shelf 2, and particle 4 in 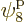 ,
which is on shelf 3. But there are a lot more system eigenfunctions
with the same shelf occupation numbers; in fact, there are
,
which is on shelf 3. But there are a lot more system eigenfunctions
with the same shelf occupation numbers; in fact, there are

such eigenfunctions, since there are 4 possible choices for the
particle that goes on shelf 1, times a remaining 3 possible choices
for the particle that goes on shelf 3, times 8 possible choices
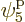 through
through 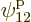 for the single-particle
eigenfunction on shelf 3 that that particle can go into, times 3
possible choices
for the single-particle
eigenfunction on shelf 3 that that particle can go into, times 3
possible choices  through
through 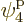 that each of the
remaining two particles on shelf 2 can go into.
that each of the
remaining two particles on shelf 2 can go into.
Next, consider a system four times as big. That means that there are
four times as many particles, so 
 16 particles, in a box that
has four times the volume. If the volume of the box becomes 4 times
as large, there are four times as many single-particle states on each
shelf, since the number of states per unit volume at a given
single-particle energy is constant, compare (6.6). Shelf 1
now has 4 states, shelf 2 has 12, and shelf 3 has 32. The number of
energy states for given shelf occupation numbers is shown as grey
tones in the middle graph of figure 11.5. Now the number
of system energy eigenfunctions that have all particles on shelf 1 is
not one, but 4
16 particles, in a box that
has four times the volume. If the volume of the box becomes 4 times
as large, there are four times as many single-particle states on each
shelf, since the number of states per unit volume at a given
single-particle energy is constant, compare (6.6). Shelf 1
now has 4 states, shelf 2 has 12, and shelf 3 has 32. The number of
energy states for given shelf occupation numbers is shown as grey
tones in the middle graph of figure 11.5. Now the number
of system energy eigenfunctions that have all particles on shelf 1 is
not one, but 4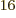 or 4 294 967 296, since there are 4
different states on shelf 1 that each of the 16 particles can go into.
That is obviously quite lot of system eigenfunctions, but it is
dwarfed by the darkest square, states with shelf occupation numbers
or 4 294 967 296, since there are 4
different states on shelf 1 that each of the 16 particles can go into.
That is obviously quite lot of system eigenfunctions, but it is
dwarfed by the darkest square, states with shelf occupation numbers
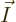
 (4,6,6). There are about 1.4 10
(4,6,6). There are about 1.4 10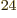 system energy
eigenfunctions with those shelf occupation numbers. So the
system energy
eigenfunctions with those shelf occupation numbers. So the 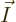
 (16,0,0) square at the origin stays lily-white despite having
over 4 billion energy eigenfunctions.
(16,0,0) square at the origin stays lily-white despite having
over 4 billion energy eigenfunctions.
If the system size is increased by another factor 4, to 64 particles,
the number of states with occupation numbers 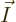
 (64,0,0),
all particles on shelf 1, is 1.2 10
(64,0,0),
all particles on shelf 1, is 1.2 10 , a tremendous number, but
totally humiliated by the 2.7 10
, a tremendous number, but
totally humiliated by the 2.7 10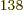 eigenfunctions that have
occupation numbers
eigenfunctions that have
occupation numbers 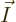
 (14,27,23). Taking the ratio of
these two numbers shows that there are 2.3 10
(14,27,23). Taking the ratio of
these two numbers shows that there are 2.3 10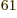 energy eigenfunctions
with shelf numbers
energy eigenfunctions
with shelf numbers 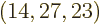 for each eigenfunction with shelf
numbers
for each eigenfunction with shelf
numbers 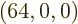 . By the time the system reaches, say, 10
. By the time the system reaches, say, 10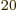 particles, still less than a millimol, the number of system energy
eigenstates for each set of occupation numbers is astronomical, but so
are the differences between the shelf numbers that have the most and
those that have less. The tick marks in figure 11.5
indicate that for large systems, the darkest square will have 40% of
the particles on shelf 2, 37% on shelf 3, and the remaining 23% on
shelf 1.
particles, still less than a millimol, the number of system energy
eigenstates for each set of occupation numbers is astronomical, but so
are the differences between the shelf numbers that have the most and
those that have less. The tick marks in figure 11.5
indicate that for large systems, the darkest square will have 40% of
the particles on shelf 2, 37% on shelf 3, and the remaining 23% on
shelf 1.
These general trends do not just apply to this simple model system;
they are typical:
The number of system energy eigenfunctions for a macroscopic
system is astronomical, and so are the differences in numbers.
Another trend illustrated by figure 11.5 has to do with the
effect of system energy. The system energy of an energy eigenfunction
is given in terms of its shelf numbers by
so all eigenfunctions with the same shelf numbers have the same system
energy. In particular, the squares just below the oblique cut-off
line in figure 11.5 have the highest system energy. It is
seen that these shelf numbers also have by far the most energy
eigenfunctions:
The number of system energy eigenfunctions with a higher energy
typically dwarfs the number of system eigenfunctions with a lower
energy.
Figure 11.6:
Number of energy eigenfunctions on the oblique energy line
in the previous figure. (The curves are mathematically
interpolated to allow a continuously varying fraction of
particles on shelf 2.) Left: 4 particles, middle: 64, right:
1,024.
![\begin{figure}\centering
{}%
\setlength{\unitlength}{1pt}
\begin{picture}(4...
...iput(110,-13)(140.3,0){3}{\makebox(0,0)[b]{$I_2/I$}}
\end{picture}
\end{figure}](img2348.gif) |
Next assume that the system has exactly the energy of the oblique
cut-off line in figure 11.5, with zero uncertainty.
The number of energy eigenstates 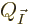 on that oblique line is
plotted in figure 11.6 as a function of the fraction of
particles
on that oblique line is
plotted in figure 11.6 as a function of the fraction of
particles 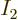

 on shelf 2. (To get a smooth continuous curve,
the values have been mathematically interpolated in between the
integer values of
on shelf 2. (To get a smooth continuous curve,
the values have been mathematically interpolated in between the
integer values of 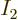 . The continuous function that
interpolates
. The continuous function that
interpolates 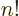 is called the gamma function; see the notations
section under
is called the gamma function; see the notations
section under !
for details.) The maximum number of
energy eigenstates occurs at about 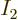


 40%,
corresponding to
40%,
corresponding to 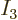
 37% and
37% and 
 23%. This set of
occupation numbers,
23%. This set of
occupation numbers,  = (0.23,0.40,0.37)
= (0.23,0.40,0.37) , is
called the
, is
called the most probable set of occupation numbers.
If
you pick an eigenfunction at random, you have more chance of getting
one with that set of occupation numbers than one with a different
given set of occupation numbers.
To be sure, if the number of particles is large, the chances of
picking any eigenfunction with an exact set of occupation
numbers is small. But note how the spike
in figure
11.6 becomes narrower with increasing number of particles.
You may not pick an eigenfunction with exactly the most
probable set of shelf numbers, but you are quite sure to pick one with
shelf numbers very close to it. By the time the system size reaches,
say, 10 particles, the spike becomes for all practical
purposes a mathematical line. Then essentially all
eigenfunctions have very precisely 23% of their particles on shelf 1
at energy
particles, the spike becomes for all practical
purposes a mathematical line. Then essentially all
eigenfunctions have very precisely 23% of their particles on shelf 1
at energy 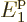 , 40% on shelf 2 at energy
, 40% on shelf 2 at energy 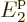 , and
37% on shelf 3 at energy
, and
37% on shelf 3 at energy 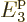 .
.
Since there is only an incredibly small fraction of eigenfunctions
that do not have very accurately the most probable occupation numbers,
it seems intuitively obvious that in thermal equilibrium, the physical
system must have the same distribution of particle energies. Why
would nature prefer one of those extremely rare eigenfunctions that do
not have these occupation numbers, rather than one of the vast
majority that do? In fact, {N.23},
It is a fundamental assumption of statistical mechanics that in
thermal equilibrium, all system energy eigenfunctions with the
same energy have the same probability.
So the most probable set of shelf numbers, as found from the count of
eigenfunctions, gives the distribution of particle energies in thermal
equilibrium.
This then is the final conclusion: the particle energy distribution of
a macroscopic system of weakly interacting particles at a given
energy can be obtained by merely counting the system energy eigenstates. It can be done without doing any physics. Whatever physics may want to do, it
is just not enough to offset the vast numerical superiority of the
eigenfunctions with very accurately the most probable shelf numbers.
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()

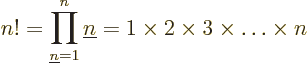

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() )
)![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![\begin{figure}\centering
{}%
\setlength{\unitlength}{1pt}
\begin{picture}(4...
...]{$I_3/I$}}
\put(278,68){\makebox(0,0)[l]{$I_3/I$}}
\end{picture}
\end{figure}](img2329.gif)
![]()
![]()
![]() ?
?![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![\begin{figure}\centering
{}%
\setlength{\unitlength}{1pt}
\begin{picture}(4...
...iput(110,-13)(140.3,0){3}{\makebox(0,0)[b]{$I_2/I$}}
\end{picture}
\end{figure}](img2348.gif)
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 2
2![]()
![]() ,
,![]()
![]() ,
,![]() ,
,![]() .
.