| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
13.5 Stern-Gerlach Apparatus
A constant magnetic field will exert a torque, but no net force on a
magnetic dipole like an electron; if you think of the dipole as a
magnetic north pole and south pole close together, the magnetic forces
on north pole and south pole will be opposite and produce no net force
on the dipole. However, if the magnetic field strength varies with
location, the two forces will be different and a net force will
result.
The Stern-Gerlach apparatus exploits this process by sending a beam of
atoms through a magnetic field with spatial variation, causing the
atoms to deflect upwards or downwards depending on their magnetic
dipole strength. The magnetic dipole strengths of the atoms will be
proportional to the relevant electron angular momenta, (the nucleus
can be ignored because of the large mass in its gyromagnetic ratio),
and that will be quantized. So the incoming beam will split into
distinct beams corresponding to the quantized values of the
electron angular momentum.
The experiment was a great step forward in the development of
quantum mechanics, because there is really no way that classical
mechanics can explain the splitting into separate beams; classical
mechanics just has to predict a smeared-out beam. Angular momentum in
classical mechanics can have any value, not just the values 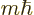 of quantum mechanics. Moreover, by capturing one of the split beams,
you have a source of particles all in the same state without
uncertainty, to use for other experiments or practical applications
such as masers.
of quantum mechanics. Moreover, by capturing one of the split beams,
you have a source of particles all in the same state without
uncertainty, to use for other experiments or practical applications
such as masers.
Stern and Gerlach used a beam of silver atoms in their experiment, and
the separated beams deposited this silver on a plate. Initially,
Gerlach had difficulty seeing any deposited silver on those plates
because the layer was extremely thin. But fortunately for quantum
mechanics, Stern was puffing his usual cheap cigars when he had a
look, and the large amount of sulphur in the smoke was enough to turn
some of the silver into jet-black silver sulfide, making it show
clearly.
An irony is that that Stern and Gerlach assumed that that they had
verified Bohr's orbital momentum. But actually, they had discovered
spin. The net magnetic moment of silver’s inner electrons is zero, and
the lone valence electron is in a 5s orbit with zero orbital angular
momentum. It was the spin of the valence electron that caused the
splitting. While spin has half the strength of orbital angular
momentum, its magnetic moment is about the same due to its  -factor
being two rather than one.
-factor
being two rather than one.
To use the Stern Gerlach procedure with charged particles such as lone
electrons, a transverse electric field must be provided to counteract
the large Lorentz force that the magnet imparts on the moving
electrons.
![]()
![]() -
-