13.6 Nuclear Magnetic Resonance

Nuclear magnetic resonance, or NMR, is a valuable tool for examining nuclei, for probing the structure of molecules, in particular organic ones, and for medical diagnosis, as MRI. This section will give a basic quantum description of the idea. Linear algebra will be used.

13.6.1 Description of the method

First demonstrated independently by Bloch and Purcell in 1946, NMR probes nuclei with net spin, in particular hydrogen nuclei or other nuclei with spin $\leavevmode\kern.03em \raise.7ex\hbox{\the\scriptfont0 1}\kern-.2em /\kern-.2em\lower.4ex\hbox{\the\scriptfont0 2}\kern.05em$. Various common nuclei, like carbon and oxygen do not have net spin; this can be a blessing since they cannot mess up the signals from the hydrogen nuclei, or a limitation, depending on how you want to look at it. In any case, if necessary isotopes such as carbon 13 can be used which do have net spin.

It is not actually the spin, but the associated magnetic dipole moment of the nucleus that is relevant, for that allows the nuclei to be manipulated by magnetic fields. First the sample is placed in an extremely strong steady magnetic field. Typical fields are in terms of Tesla. (A Tesla is about 20,000 times the strength of the magnetic field of the earth.) In the field, the nucleus has two possible energy states; a ground state in which the spin component in the direction of the magnetic field is aligned with it, and an elevated energy state in which the spin is opposite {N.33}. (Despite the large field strength, the energy difference between the two states is extremely small compared to the thermal kinetic energy at room temperature. The number of nuclei in the ground state may only exceed those in the elevated energy state by say one in 100,000, but that is still a large absolute number of nuclei in a sample.)

Now perturb the nuclei with a second, much smaller and radio frequency, magnetic field. If the radio frequency is just right, the excess ground state nuclei can be lifted out of the lowest energy state, absorbing energy that can be observed. The “resonance” frequency at which this happens then gives information about the nuclei. In order to observe the resonance frequency very accurately, the perturbing rf field must be very weak compared to the primary steady magnetic field.

In Continuous Wave NMR, the perturbing frequency is varied and the absorption examined to find the resonance. (Alternatively, the strength of the primary magnetic field can be varied, that works out to the same thing using the appropriate formula.)

In Fourier Transform NMR, the perturbation is applied in a brief pulse just long enough to fully lift the excess nuclei out of the ground state. Then the decay back towards the original state is observed. An experienced operator can then learn a great deal about the environment of the nuclei. For example, a nucleus in a molecule will be shielded a bit from the primary magnetic field by the rest of the molecule, and that leads to an observable frequency shift. The amount of the shift gives a clue about the molecular structure at the nucleus, so information about the molecule. Additionally, neighboring nuclei can cause resonance frequencies to split into several through their magnetic fields. For example, a single neighboring perturbing nucleus will cause a resonance frequency to split into two, one for spin up of the neighboring nucleus and one for spin down. It is another clue about the molecular structure. The time for the decay back to the original state to occur is another important clue about the local conditions the nuclei are in, especially in MRI. The details are beyond this author's knowledge; the purpose here is only to look at the basic quantum mechanics behind NMR.

13.6.2 The Hamiltonian

The magnetic fields will be assumed to be of the form

$$\skew2\vec{\cal B}= {\cal B}_0 {\hat k} + {\cal B}_1 \... ...{\hat\imath}\cos\omega t - {\hat\jmath}\sin\omega t\right) %$$ (13.44)

where ${\cal B}_0$ is the Tesla-strength primary magnetic field, ${\cal B}_1$ the very weak perturbing field strength, and $\omega$ is the frequency of the perturbation.

The component of the magnetic field in the $xy$-plane, ${\cal B}_1$, rotates around the $z$-axis at angular velocity $\omega$. Such a rotating magnetic field can be achieved using a pair of properly phased coils placed along the $x$ and $y$ axes. (In Fourier Transform NMR, a single perturbation pulse actually contains a range of different frequencies $\omega$, and Fourier transforms are used to take them apart.) Since the apparatus and the wave length of a radio frequency field is very large on the scale of a nucleus, spatial variations in the magnetic field can be ignored.

Now suppose you place a spin $\leavevmode\kern.03em \raise.7ex\hbox{\the\scriptfont0 1}\kern-.2em /\kern-.2em\lower.4ex\hbox{\the\scriptfont0 2}\kern.05em$ nucleus in the center of this magnetic field. As discussed in section 13.4, a particle with spin will act as a little compass needle, and its energy will be lowest if it is aligned with the direction of the ambient magnetic field. In particular, the energy is given by

$$H = - \vec \mu \cdot \skew2\vec{\cal B}$$

where $\vec\mu$ is called the magnetic dipole strength of the nucleus. This dipole strength is proportional to its spin angular momentum ${\skew 6\widehat{\vec S}}$:

$$\vec \mu = \gamma {\skew 6\widehat{\vec S}}$$

where the constant of proportionality $\gamma$ is called the gyromagnetic ratio. The numerical value of the gyromagnetic ratio can be found as

$$\gamma = \frac{g q}{2 m}$$

In case of a hydrogen nucleus, a proton, the mass $m_{\rm p}$ and charge $q_p=e$ can be found in the notations section, and the proton's experimentally found $g$-factor is $g_p=5.59$.

The bottom line is that you can write the Hamiltonian of the interaction of the nucleus with the magnetic field in terms of a numerical gyromagnetic ratio value, spin, and the magnetic field:

$$H = - \gamma {\skew 6\widehat{\vec S}}\cdot \skew2\vec{\cal B} %$$ (13.45)

Now turning to the wave function of the nucleus, it can be written as a combination of the spin-up and spin-down states,

$$\Psi= a{\uparrow}+b{\downarrow},$$

where ${\uparrow}$ has spin $\frac12\hbar$ in the $z$-direction, along the primary magnetic field, and ${\downarrow}$ has $-\frac12\hbar$. Normally, $a$ and $b$ would describe the spatial variations, but spatial variations are not relevant to the analysis, and $a$ and $b$ can be considered to be simple numbers.

You can use the concise notations of linear algebra by combining $a$ and $b$ in a two-component column vector (more precisely, a spinor),

$$\Psi = \left(\begin{array}{c}a\\ b\end{array}\right)$$

In those terms, the spin operators become matrices, the so-called Pauli spin matrices of section 12.10,

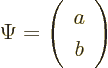
$${\widehat S}_x = \frac{\hbar}{2} \left(\begin{array}{rr}... ...2} \left(\begin{array}{rr} 1 & 0\\ 0 & -1\end{array}\right)$$ (13.46)

Substitution of these expressions for the spin, and (13.44) for the magnetic field into (13.45) gives after cleaning up the final Hamiltonian:

$$H = - \frac{\hbar}2 \left( \begin{array}{cc} \omeg... ...0 = \gamma {\cal B}_0 \quad \omega_1 = \gamma {\cal B}_1 %$$ (13.47)

The constants $\omega_0$ and $\omega_1$ have the dimensions of a frequency; $\omega_0$ is called the “Larmor frequency.” As far as $\omega_1$ is concerned, the important thing to remember is that it is much smaller than the Larmor frequency $\omega_0$ because the perturbation magnetic field is small compared to the primary one.

13.6.3 The unperturbed system

Before looking at the perturbed case, it helps to first look at the unperturbed solution. If there is just the primary magnetic field affecting the nucleus, with no radio-frequency perturbation $\omega_1$, the Hamiltonian derived in the previous subsection simplifies to

$$H = -\frac{\hbar}2 \left( \begin{array}{cc} \omega_0 & 0 \\ 0 & -\omega_0 \end{array} \right)$$

The energy eigenstates are the spin-up state, with energy $-\frac12\hbar\omega_0$, and the spin-down state, with energy $\frac12\hbar\omega_0$.

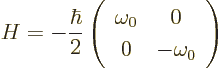
The difference in energy is in relativistic terms exactly equal to a photon with the Larmor frequency $\omega_0$. While the treatment of the electromagnetic field in this discussion will be classical, rather than relativistic, it seems clear that the Larmor frequency must play more than a superficial role.

The unsteady Schrödinger equation tells you that the wave function evolves in time like ${\rm i}\hbar\dot\Psi= H\Psi$, so if $\Psi=a{\uparrow}+b{\downarrow}$,

$${\rm i}\hbar\left(\begin{array}{c}\dot a\\ \dot b\end{arra... ...ay} \right) \left(\begin{array}{c}a\\ b\end{array}\right)$$

The solution for the coefficients $a$ and $b$ of the spin-up and -down states is:

$$a = a_0 e^{{\rm i}\omega_0 t/2} \qquad b = b_0 e^{-{\rm i}\omega_0 t/2}$$

if $a_0$ and $b_0$ are the values of these coefficients at time zero.

Since $\vert a\vert^2=\vert a_0\vert^2$ and $\vert b\vert^2=\vert b_0\vert^2$ at all times, the probabilities of measuring spin-up or spin-down do not change with time. This was to be expected, since spin-up and spin-down are energy states for the steady system. To get more interesting physics, you really need the unsteady perturbation.

But first, to understand the quantum processes better in terms of the ideas of nonquantum physics, it will be helpful to write the unsteady quantum evolution in terms of the expectation values of the angular momentum components. The expectation value of the $z$-component of angular momentum is

$$\langle S_z\rangle = \vert a\vert^2 \frac{\hbar}{2} - \vert b\vert^2 \frac{\hbar}{2}$$

To more clearly indicate that the value must be in between $-\hbar/2$ and $\hbar/2$, you can write the magnitude of the coefficients in terms of an angle $\alpha$, the “precession angle”,

$$\vert a\vert = \vert a_0\vert \equiv \cos(\alpha/2) \qquad \vert b\vert = \vert b_0\vert \equiv \sin(\alpha/2)$$

In terms of the so-defined $\alpha$, you simply have, using the half-angle trig formulae,

$$\langle S_z\rangle = \frac{\hbar}{2} \cos\alpha$$

The expectation values of the angular momenta in the $x$- and $y$-directions can by found as the inner products $\langle\Psi\vert{\widehat S}_x\Psi\rangle$ and $\langle\Psi\vert{\widehat S}_y\Psi\rangle$, chapter 4.4.3. Substituting the representation in terms of spinors and Pauli spin matrices, and cleaning up using the Euler formula (2.5), you get

$$\langle S_x\rangle = \frac{\hbar}{2} \sin\alpha \cos(\omeg... ...rangle = - \frac{\hbar}{2} \sin\alpha \sin(\omega_0 t+\alpha)$$

where $\alpha$ is some constant phase angle that is further unimportant.

The first thing that can be seen from these results is that the length of the expectation angular momentum vector is $\hbar/2$. Next, the component with the $z$-axis, the direction of the primary magnetic field, is at all times $\frac12\hbar\cos\alpha$. That implies that the expectation angular momentum vector is under a constant angle $\alpha$ with the primary magnetic field.

Figure 13.18: Larmor precession of the expectation spin (or magnetic moment) vector around the magnetic field.

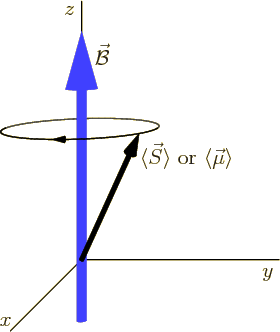The component in the $x,y$-plane is $\frac12\hbar\sin\alpha$, and this component rotates around the $z$-axis, as shown in figure 13.18, causing the end point of the expectation angular momentum vector to sweep out a circular path around the magnetic field $\skew2\vec{\cal B}$. This rotation around the $z$-axis is called “Larmor precession.” Since the magnetic dipole moment is proportional to the spin, it traces out the same conical path.

Caution should be used against attaching too much importance to this classical picture of a precessing magnet. The expectation angular momentum vector is not a physically measurable quantity. One glaring inconsistency in the expectation angular momentum vector versus the true angular momentum is that the square magnitude of the expectation angular momentum vector is $\hbar^2/4$, three times smaller than the true square magnitude of angular momentum.

13.6.4 Effect of the perturbation

In the presence of the perturbing magnetic field, the unsteady Schrödinger equation ${\rm i}\hbar\dot\Psi= H\Psi$ becomes

$${\rm i}\hbar\left(\begin{array}{c}\dot a\\ \dot b\end{arra... ... \right) \left(\begin{array}{c}a\\ b\end{array}\right) %$$ (13.48)

where $\omega_0$ is the Larmor frequency, $\omega$ is the frequency of the perturbation, and $\omega_1$ is a measure of the strength of the perturbation and small compared to $\omega_0$.

The above equations can be solved exactly using standard linear algebra procedures, though the the algebra is fairly stifling {D.77}. The analysis brings in an additional quantity that will be called the “resonance factor”

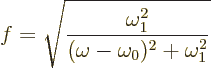$$f = \sqrt{\frac{\omega_1^2}{(\omega - \omega_0)^2 + \omega_1^2}}$$ (13.49)

Note that $f$ has its maximum value, one, at “resonance,” i.e. when the perturbation frequency $\omega$ equals the Larmor frequency $\omega_0$.

The analysis finds the coefficients of the spin-up and spin-down states to be:

$$a = \left[ a_0 \left( \cos\bigg(\frac{\omega_1 t}{2f}\bigg) -... ...\sin\bigg(\frac{\omega_1 t}{2f}\bigg) \right] e^{{\rm i}\omega t/2}\quad\quad$$ (13.50)

$$b = \left[ b_0 \left( \cos\bigg(\frac{\omega_1 t}{2f}\bigg) +... ...sin\bigg(\frac{\omega_1 t}{2f}\bigg) \right] e^{-{\rm i}\omega t/2}\quad\quad$$ (13.51)

where $a_0$ and $b_0$ are the initial coefficients of the spin-up and spin-down states.

This solution looks pretty forbidding, but it is not that bad in application. The primary interest is in nuclei that start out in the spin-up ground state, so you can set $\vert a_0\vert=1$ and $b_0=0$. Also, the primary interest is in the probability that the nuclei may be found at the elevated energy level, which is

$$\vert b\vert^2 = f^2 \sin^2\bigg(\frac{\omega_1 t}{2f}\bigg)$$ (13.52)

That is a pretty simple result. When you start out, the nuclei you look at are in the ground state, so $\vert b\vert^2$ is zero, but with time the rf perturbation field increases the probability of finding the nuclei in the elevated energy state eventually to a maximum of $f^2$ when the sine becomes one.

Figure 13.19: Probability of being able to find the nuclei at elevated energy versus time for a given perturbation frequency $\omega$.

Continuing the perturbation beyond that time is bad news; it decreases the probability of elevated states again. As figure 13.19 shows, over extended times, there is a flip-flop between the nuclei being with certainty in the ground state, and having a probability of being in the elevated state. The frequency at which the probability oscillates is called the “Rabi flopping frequency”. The author’s sources differ about the precise definition of this frequency, but the one that seems to be most logical is $\omega_1/f$.

Figure 13.20: Maximum probability of finding the nuclei at elevated energy.

Anyway, by keeping up the perturbation for the right time you can raise the probability of elevated energy to a maximum of $f^2$. A plot of $f^2$ against the perturbing frequency $\omega$ is called the “resonance curve,“ shown in figure 13.20. For the perturbation to have maximum effect, its frequency $\omega$ must equal the nuclei's Larmor frequency $\omega_0$. Also, for this frequency to be very accurately observable, the “spike” in figure 13.20 must be narrow, and since its width is proportional to $\omega_1=\gamma{\cal B}_1$, that means the perturbing magnetic field must be very weak compared to the primary magnetic field.

Figure 13.21: A perturbing magnetic field, rotating at precisely the Larmor frequency, causes the expectation spin vector to come cascading down out of the ground state.

There are two qualitative ways to understand the need for the frequency of the perturbation to equal the Larmor frequency. One is geometrical and classical: as noted in the previous subsection, the expectation magnetic moment precesses around the primary magnetic field with the Larmor frequency. In order for the small perturbation field to exert a long-term downward “torque” on this precessing magnetic moment as in figure 13.21, it must rotate along with it. If it rotates at any other frequency, the torque will quickly reverse direction compared to the magnetic moment, and the vector will start going up again. The other way to look at it is from a relativistic quantum perspective: if the magnetic field frequency equals the Larmor frequency, its photons have exactly the energy required to lift the nuclei from the ground state to the excited state.

At the Larmor frequency, it would naively seem that the optimum time to maintain the perturbation is until the expectation spin vector is vertically down; then the nucleus is in the exited energy state with certainty. If you then allow nature the time to probe its state, every nucleus will be found to be in the excited state, and will emit a photon. (If not messed up by some collision or whatever, little in life is ideal, is it?) However, according to actual descriptions of NMR devices, it is better to stop the perturbation earlier, when the expectation spin vector has become horizontal, rather than fully down. In that case, nature will only find half the nuclei in the excited energy state after the perturbation, presumably decreasing the radiation yield by a factor 2. The classical explanation that is given is that when the (expectation) spin vector is precessing at the Larmor frequency in the horizontal plane, the radiation is most easily detected by the coils located in that same plane. And that closes this discussion.