| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
12.6 Triplet and singlet states
With the ladder operators, you can determine how different angular
momenta add up to net angular momentum. As an example, this section
will examine what net spin values can be produced by two particles,
each with spin  . They may be the proton and electron
in a hydrogen atom, or the two electrons in the hydrogen molecule, or
whatever. The actual result will be to rederive the triplet and
singlet states described in chapter 5.5.6, but it will
also be an example for how more complex angular momentum states can be
combined.
. They may be the proton and electron
in a hydrogen atom, or the two electrons in the hydrogen molecule, or
whatever. The actual result will be to rederive the triplet and
singlet states described in chapter 5.5.6, but it will
also be an example for how more complex angular momentum states can be
combined.
The particles involved will be denoted as  and
and 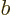 . Since
each particle can have two different spin states
. Since
each particle can have two different spin states  and
and
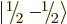 , there are four different combined
, there are four different combined
product
states:
In these product states, each particle is in a single individual spin
state. The question is, what is the combined angular momentum of
these four product states? And what combination states have
definite net values for square and  angular momentum?
angular momentum?
The angular momentum in the  -direction is simple; it is just the
sum of those of the individual particles. For example, the
-direction is simple; it is just the
sum of those of the individual particles. For example, the
 -momentum of the
-momentum of the 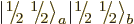 state follows from
state follows from
which makes the net angular momentum in the  -direction
-direction
 , or
, or  from each particle. Note that the
from each particle. Note that the
 angular momentum operators of the two particles simply add up and
that
angular momentum operators of the two particles simply add up and
that 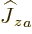 only acts on particle
only acts on particle  , and
, and
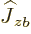 only on particle
only on particle 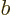 {N.28}. In
terms of quantum numbers, the magnetic quantum number
{N.28}. In
terms of quantum numbers, the magnetic quantum number 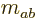 is the
sum of the individual quantum numbers
is the
sum of the individual quantum numbers 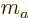 and
and 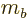 ;
; 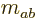


 1.
1.
The net total angular momentum is not so obvious; you cannot just add
total angular momenta. To figure out the total angular momentum of
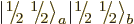 anyway, there is a trick: multiply it with the
combined step-up operator
anyway, there is a trick: multiply it with the
combined step-up operator
Each part returns zero: 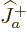 because particle
because particle  is at the top of
its ladder and
is at the top of
its ladder and 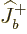 because particle
because particle 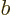 is. So the combined
state
is. So the combined
state 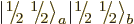 must be at the top of the ladder too;
there is no higher rung. That must mean
must be at the top of the ladder too;
there is no higher rung. That must mean 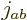

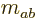
 1; the combined state must be a
1; the combined state must be a 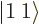 state. It can be
defined it as the combination
state. It can be
defined it as the combination 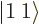 state:
state:
 |
(12.11) |
You could just as well have defined  as
as
 or
or 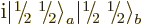 , say. But
why drag along a minus sign or
, say. But
why drag along a minus sign or  if you do not have to? The first
triplet state has been found.
if you do not have to? The first
triplet state has been found.
Here is another trick: multiply 

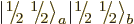 by
by 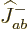 : that will go one step
down the combined states ladder and produce a combination state
: that will go one step
down the combined states ladder and produce a combination state
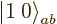 :
:
or
where the effects of the ladder-down operators were taken from
(12.10). (Note that this requires that the individual
particle spin states are normalized consistent with the ladder
operators.) The second triplet state is therefore:
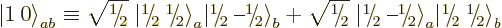 |
(12.12) |
But this gives only one 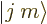 combination state for the
two product states
combination state for the
two product states 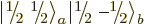 and
and
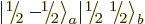 with zero net
with zero net  -momentum. If you
want to describe unequal combinations of them, like
-momentum. If you
want to describe unequal combinations of them, like
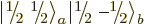 by itself, it cannot be just a multiple of
by itself, it cannot be just a multiple of
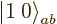 . This suggests that there may be another
. This suggests that there may be another
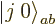 combination state involved here. How do you get this
second state?
combination state involved here. How do you get this
second state?
Well, you can reuse the first trick. If you construct a combination
of the two product states that steps up to zero, it must be a state
with zero  angular momentum that is at the end of its ladder, a
angular momentum that is at the end of its ladder, a
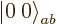 state. Consider an arbitrary combination of the two
product states with as yet unknown numerical coefficients
state. Consider an arbitrary combination of the two
product states with as yet unknown numerical coefficients 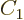 and
and
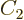 :
:
For this combination to step up to zero,
must be zero, which requires 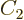

 , leaving
, leaving 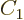 undetermined.
undetermined. 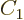 must be chosen such that the state is normalized,
but that still leaves a constant of magnitude one undetermined. To
fix it,
must be chosen such that the state is normalized,
but that still leaves a constant of magnitude one undetermined. To
fix it, 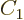 is taken to be real and positive, and so the singlet
state becomes
is taken to be real and positive, and so the singlet
state becomes
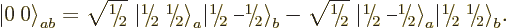 |
(12.13) |
To find the remaining triplet state,
just apply 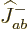 once more, to
once more, to 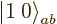 above. It gives:
above. It gives:
![\begin{displaymath}
{{\left\vert 1\:\rule[2.5pt]{5pt}{.5pt}1\right\rangle}}_{ab...
...r.56ex\hbox{\the\scriptfont0 2}\kern.05em\right\rangle}}_{b} %
\end{displaymath}](img2732.gif) |
(12.14) |
Of course, the normalization factor of this bottom state had to turn
out to be one; all three step-down operators produce only positive
real factors.
Figure 12.3:
Triplet and singlet states in terms of ladders
![\begin{figure}\centering
\setlength{\unitlength}{1pt}
\resizebox{5.6truein}{...
...r:\\ [-4pt]
\strut $j_{ab}=0$}}}
\end{picture} }
\end{picture}}
\end{figure}](img2733.gif) |
Figure 12.3 shows the results graphically in terms of
ladders. The two possible spin states of each of the two electrons
produce 4 combined product states indicated using up and down arrows.
These product states are then combined to produce triplet and singlet
states that have definite values for both  and total net
angular momentum, and can be shown as rungs on ladders.
and total net
angular momentum, and can be shown as rungs on ladders.
Note that a product state like 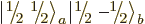 cannot be shown
as a rung on a ladder. In fact, from adding (12.12) and
(12.13) it is seen that
cannot be shown
as a rung on a ladder. In fact, from adding (12.12) and
(12.13) it is seen that
which makes it a combination of the middle rungs of the triplet and
singlet ladders, rather than a single rung.
![]() .
.![]()
![]() .
.![]()
![]() ,
,![]() -
-![]() -
-![]()

![]()
![]()
![]()
![]()
![]() :
:![]() :
:
![]()
![]()
![]()
![]() -
-![]()
![]() .
.![]()
![]()
![]()
![]()
![]() :
: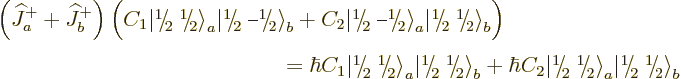
![]()
![]()
![]()
![]()