| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
12.5 A warning about angular momentum
Normally, eigenstates are indeterminate by a complex number of
magnitude one. If you so desire, you can multiply any normalized
eigenstate by a number of unit magnitude of your own choosing, and it
is still a normalized eigenstate. It is important to remember that in
analytical expressions involving angular momentum, you are not
allowed to do this.
As an example, consider a pair of spin 1/2 particles, call them  and
and 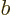 , in the
, in the singlet state
, in which their
spins cancel and there is no net angular momentum. It was noted in
chapter 5.5.6 that this state takes the form
(This section will use kets rather than arrows for spin states.) But
if you were allowed to arbitrarily change the definition of say the
spin state 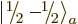 by a minus sign, then the minus sign in the
singlet state above would turn in a plus sign. The given expression
for the singlet state, with its minus sign, is only correct if you use
the right normalization factors for the individual states.
by a minus sign, then the minus sign in the
singlet state above would turn in a plus sign. The given expression
for the singlet state, with its minus sign, is only correct if you use
the right normalization factors for the individual states.
It all has to do with the ladder operators 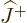 and
and 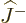 .
They are very convenient for analysis, but to make that easiest, you
would like to know exactly what they do to the angular momentum
states
.
They are very convenient for analysis, but to make that easiest, you
would like to know exactly what they do to the angular momentum
states 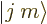 . What you have seen so far is that
. What you have seen so far is that
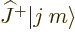 produces a state with the same square angular momentum,
and with angular momentum in the
produces a state with the same square angular momentum,
and with angular momentum in the  -direction equal to
-direction equal to
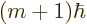 . In other words,
. In other words, 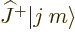 is some multiple of
a suitably normalized eigenstate
is some multiple of
a suitably normalized eigenstate  ;
;
where the number 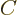 is the multiple. What is that multiple?
Well, from the magnitude of
is the multiple. What is that multiple?
Well, from the magnitude of 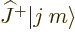 , derived earlier in
(12.6) you know that its square magnitude is
, derived earlier in
(12.6) you know that its square magnitude is
But that still leaves 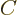 indeterminate by a factor of
unit magnitude. Which would be very inconvenient in the analysis
of angular momentum.
indeterminate by a factor of
unit magnitude. Which would be very inconvenient in the analysis
of angular momentum.
To resolve this conundrum, restrictions are put on the normalization
factors of the angular momentum states 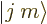 in ladders. It is
required that the normalization factors are chosen such that the
ladder operator constants are positive real numbers. That really
leaves only one normalization factor in an entire ladder freely
selectable, say the one of the top rung.
in ladders. It is
required that the normalization factors are chosen such that the
ladder operator constants are positive real numbers. That really
leaves only one normalization factor in an entire ladder freely
selectable, say the one of the top rung.
Most of the time, this is not a big deal. Only when you start trying
to get too clever with angular momentum normalization factors, then
you want to remember that you cannot really choose them to your own
liking.
The good news is that in this convention, you know precisely
what the ladder operators do {D.64}:
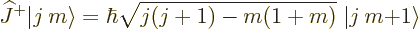 |
(12.9) |
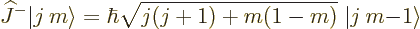 |
(12.10) |
![]()
![]() ,
,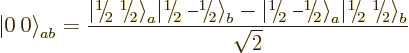
![]()
![]() .
.![]() .
.![]()
![]() -
-![]() .
.![]()
![]() ;
;![]()