| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
6.12 Confinement and the DOS
The motion of a single particle in a confining box was described in
chapter 3.5.9. Nontrivial motion in a direction in which
the box is sufficiently narrow can become impossible. This section
looks at what happens to the density of states for such a box. The
density of states gives the number of single-particle states per unit
energy range. It is interesting for many reasons. For example, for
systems of electrons the density of states at the Fermi energy
determines how many electrons in the box pick up thermal energy if the
temperature is raised above zero. It also determines how many
electrons will be involved in electrical conduction if their energy is
raised.
By definition, the density of states 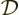 gives the number of
single-particle states
gives the number of
single-particle states 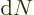 in an energy range from
in an energy range from 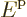 to
to
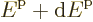 as
as
where 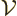 is the volume of the box containing the particles. To
use this expression, the size of the energy range
is the volume of the box containing the particles. To
use this expression, the size of the energy range 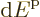 should be
small, but still big enough that the number of states
should be
small, but still big enough that the number of states 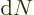 in it
remains large.
in it
remains large.
For a box that is not confining, the density of states is proportional
to  . To understand why, consider first the total
number of states
. To understand why, consider first the total
number of states 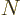 that have energy less than some given value
that have energy less than some given value
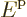 . For example, the wave number space to the left in figure
6.11 shows all states with energy less than the Fermi energy
in red. Clearly, the number of such states is about proportional to
the volume of the octant of the sphere that holds them. And that
volume is in turn proportional to the cube of the sphere radius
. For example, the wave number space to the left in figure
6.11 shows all states with energy less than the Fermi energy
in red. Clearly, the number of such states is about proportional to
the volume of the octant of the sphere that holds them. And that
volume is in turn proportional to the cube of the sphere radius
 , which is proportional to
, which is proportional to  ,
(6.4), so
,
(6.4), so
This gives the number of states that have energies less than some
value 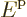 . To get the number of states in an energy range
from
. To get the number of states in an energy range
from 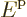 to
to 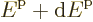 , take a differential:
, take a differential:
So the density of states is proportional to  . (The
constant of proportionality is worked out in derivation
{D.26}.) This density of states is shown as the width
of the energy spectrum to the right in figure 6.11.
. (The
constant of proportionality is worked out in derivation
{D.26}.) This density of states is shown as the width
of the energy spectrum to the right in figure 6.11.
Figure 6.12:
Severe
confinement in the  -direction, as in a quantum well.
-direction, as in a quantum well.
![\begin{figure}\centering
\setlength{\unitlength}{1pt}
\begin{picture}(405,20...
...7.5,135){\makebox(0,0)[r]{${\vphantom' E}^{\rm p}$}}
\end{picture}
\end{figure}](img1354.gif) |
Confinement changes the spacing between the states. Consider first
the case that the box containing the particles is very narrow in the
 -direction only. That produces a quantum well, in which
motion in the
-direction only. That produces a quantum well, in which
motion in the  -direction is inhibited. In wave number space
the states become spaced very far apart in the
-direction is inhibited. In wave number space
the states become spaced very far apart in the 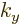 -direction.
That is illustrated to the left in figure 6.12. The red
states are again the ones with an energy below some given example
value
-direction.
That is illustrated to the left in figure 6.12. The red
states are again the ones with an energy below some given example
value 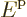 , say the Fermi energy. Clearly, now the number of
states inside the red sphere is proportional not to its volume,
but to the area of the quarter circle holding the red
states. The density of states changes correspondingly, as shown to
the right in figure 6.12.
, say the Fermi energy. Clearly, now the number of
states inside the red sphere is proportional not to its volume,
but to the area of the quarter circle holding the red
states. The density of states changes correspondingly, as shown to
the right in figure 6.12.
Consider the variation in the density of states for energies starting
from zero. As long as the energy is less than that of the smaller
blue sphere in figure 6.12, there are no states at or below
that energy, so there is no density of states either. However, when
the energy becomes just a bit higher than that of the smaller blue
sphere, the sphere gobbles up quite a lot of states compared to the
small box volume. That causes the density of states to jump up.
However, after that jump, the density of states does not continue grow
like the unconfined case. The unconfined case keeps gobbling up more
and more circles of states when the energy grows. The confined case
remains limited to a single circle until the energy hits that of the
larger blue sphere. At that point, the density of states jumps up
again. Through jumps like that, the confined density of states
eventually starts resembling the unconfined case when the energy
levels get high enough.
As shown to the right in the figure, the density of states is
piecewise constant for a quantum well. To understand why, note that
the number of states on a circle is proportional to its square radius
 . That is the same as
. That is the same as  , and
, and 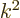 is directly proportional to the energy
is directly proportional to the energy 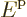 . So the number of
states varies linearly with energy, making its derivative, the density
of states, constant. (The detailed mathematical expressions for the
density of states for this case and the ones below can again be found
in derivation {D.26}.)
. So the number of
states varies linearly with energy, making its derivative, the density
of states, constant. (The detailed mathematical expressions for the
density of states for this case and the ones below can again be found
in derivation {D.26}.)
Figure 6.13:
Severe confinement in both the  and
and  directions, as in a quantum wire.
directions, as in a quantum wire.
![\begin{figure}\centering
\setlength{\unitlength}{1pt}
\begin{picture}(405,20...
...304,135){\makebox(0,0)[r]{${\vphantom' E}^{\rm p}$}}
\end{picture}
\end{figure}](img1357.gif) |
The next case is that the box is very narrow in the  -direction as
well as in the
-direction as
well as in the  -direction. This produces a quantum wire, where
there is full freedom of motion only in the
-direction. This produces a quantum wire, where
there is full freedom of motion only in the  -direction. This case
is shown in figure 6.13. Now the states separate into
individual lines of states. The smaller blue sphere just reaches the
line of states closest to the origin. There are no energy states
until the energy exceeds the level of this blue sphere. Just above
that level, a lot of states are encountered relative to the very small
box volume, and the density of states jumps way up. When the energy
increases further, however, the density of states comes down again:
compared to the less confined cases, no new lines of states are added
until the energy hits the level of the larger blue sphere. When the
latter happens, the density of states jumps way up once again.
Mathematically, the density of states produced by each line is
proportional to the reciprocal square root of the excess energy above the
one needed to reach the line.
-direction. This case
is shown in figure 6.13. Now the states separate into
individual lines of states. The smaller blue sphere just reaches the
line of states closest to the origin. There are no energy states
until the energy exceeds the level of this blue sphere. Just above
that level, a lot of states are encountered relative to the very small
box volume, and the density of states jumps way up. When the energy
increases further, however, the density of states comes down again:
compared to the less confined cases, no new lines of states are added
until the energy hits the level of the larger blue sphere. When the
latter happens, the density of states jumps way up once again.
Mathematically, the density of states produced by each line is
proportional to the reciprocal square root of the excess energy above the
one needed to reach the line.
Figure 6.14:
Severe
confinement in all three directions, as in a quantum dot or
artificial atom.
![\begin{figure}\centering
\setlength{\unitlength}{1pt}
\begin{picture}(405,20...
...304,135){\makebox(0,0)[r]{${\vphantom' E}^{\rm p}$}}
\end{picture}
\end{figure}](img1358.gif) |
The final possibility is that the box holding the particles is very
narrow in all three directions. This produces a quantum dot or
artificial atom. Now each energy state is a separate point, figure
6.14. The density of states is now zero unless the energy
sphere exactly hits one of the individual points, in which case the
density of states is infinite. So, the density of states is a set of
spikes. Mathematically, the contribution of each state to the density
of states is a delta function located at that energy.
(It may be pointed out that very strictly speaking, every density of
states is a set of delta functions. After all, the individual states
always remain discrete points, however extremely densely spaced they
might be. Only if you average the delta functions over a small energy
range 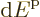 do you get the smooth mathematical functions of the
quantum wire, quantum well, and unconfined box. It is no big deal, as
a perfect confining box does not exist anyway. In real life, energy
spikes do broaden out bit; there is always some uncertainty in energy
due to various effects.)
do you get the smooth mathematical functions of the
quantum wire, quantum well, and unconfined box. It is no big deal, as
a perfect confining box does not exist anyway. In real life, energy
spikes do broaden out bit; there is always some uncertainty in energy
due to various effects.)
Key Points

- If one or more dimensions of a box holding a system of particles
becomes very small, confinement effects show up.

- In particular, the density of states shows a staging behavior
that is typical for each reduced dimensionality.
![]()
![]()
![]()
![]()
![]() .
.![]()
![]() .
.![]() ,
,![]() ,
,![]() -
-![]() -
-![]() -
-![]() ,
,![]() .
.![]() ,
,![]()
![]() .
.![]() -
-![]() -
-![]() -
-![\begin{figure}\centering
\setlength{\unitlength}{1pt}
\begin{picture}(405,20...
...304,135){\makebox(0,0)[r]{${\vphantom' E}^{\rm p}$}}
\end{picture}
\end{figure}](img1358.gif)
![]()