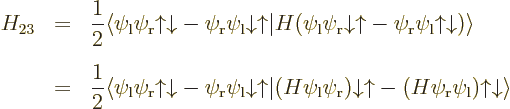| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
5.8 Matrix Formulation
When the number of unknowns in a quantum mechanical problem has been
reduced to a finite number, the problem can be reduced to a linear
algebra one. This allows the problem to be solved using standard
analytical or numerical techniques. This section describes how the
linear algebra problem can be obtained.
Typically, quantum mechanical problems can be reduced to a finite
number of unknowns using some finite set of chosen wave functions, as
in the previous section. There are other ways to make the problems
finite, it does not really make a difference here. But in general
some simplification will still be needed afterwards. A multiple sum
like equation (5.30) for distinguishable particles is
awkward to work with, and when various coefficients drop out for
identical particles, its gets even messier. So as a first step, it is
best to order the terms involved in some way; any ordering will in
principle do. Ordering allows each term to be indexed by a single
counter  , being the place of the term in the ordering.
, being the place of the term in the ordering.
Using an ordering, the wave function for a total of  particles can
be written more simply as
particles can
be written more simply as
or in index notation:
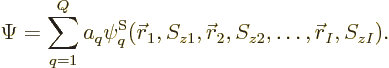 |
(5.32) |
where  is the total count of the chosen
is the total count of the chosen  -particle wave
functions and the single counter
-particle wave
functions and the single counter  in
in 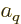 replaces a set of
replaces a set of  indices in the description used in the previous section. The
indices in the description used in the previous section. The
 -particle functions
-particle functions  are allowed to be anything;
individual (Hartree) products of single-particle wave functions for
distinguishable particles as in (5.30), Slater determinants
for identical fermions, permanents for identical bosons, or whatever.
The only thing that will be assumed is that they are mutually
orthonormal. (Which means that any underlying set of single-particle
functions
are allowed to be anything;
individual (Hartree) products of single-particle wave functions for
distinguishable particles as in (5.30), Slater determinants
for identical fermions, permanents for identical bosons, or whatever.
The only thing that will be assumed is that they are mutually
orthonormal. (Which means that any underlying set of single-particle
functions 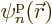 as described in the previous section should
be orthonormal. If they are not, there are procedures like
Gram-Schmidt to make them so. Or you can just put in some correction
terms.)
as described in the previous section should
be orthonormal. If they are not, there are procedures like
Gram-Schmidt to make them so. Or you can just put in some correction
terms.)
Under those conditions, the energy eigenvalue problem 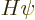

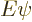 takes the form:
takes the form:
The trick is now to take the inner product of both sides of this
equation with each function 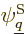 in the set of wave
functions in turn. In other words, take an inner product with
in the set of wave
functions in turn. In other words, take an inner product with
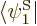 to get one equation, then take an inner product with
to get one equation, then take an inner product with
 to get a second equation, and so on. This produces,
using the fact that the functions are orthonormal to clean up the
right-hand side,
to get a second equation, and so on. This produces,
using the fact that the functions are orthonormal to clean up the
right-hand side,
where
are the matrix coefficients, or Hamiltonian coefficients.
This can again be written more compactly in index notation:
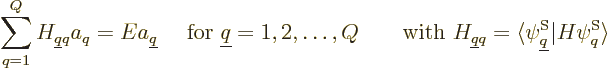 |
(5.33) |
which is just a finite-size matrix eigenvalue problem.
Since the functions 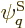 are known, chosen, functions, and the
Hamiltonian
are known, chosen, functions, and the
Hamiltonian 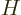 is also known, the matrix coefficients
is also known, the matrix coefficients 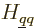 can be determined. The eigenvalues
can be determined. The eigenvalues
 and corresponding eigenvectors
and corresponding eigenvectors  can then be
found using linear algebra procedures. Each eigenvector produces a
corresponding approximate eigenfunction
can then be
found using linear algebra procedures. Each eigenvector produces a
corresponding approximate eigenfunction 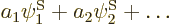 with an energy equal to the eigenvalue
with an energy equal to the eigenvalue  .
.
Key Points

- Operator eigenvalue problems can be approximated by the matrix
eigenvalue problems of linear algebra.

- That allows standard analytical or numerical techniques to be
used in their solution.
5.8 Review Questions
-
1.
-
As a relatively simple example, work out the above ideas for the 
 2 hydrogen molecule spatial states
2 hydrogen molecule spatial states 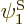

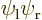 and
and 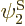

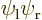 . Write the matrix eigenvalue problem and identify the two eigenvalues and eigenvectors. Compare with the results of section 5.3.
. Write the matrix eigenvalue problem and identify the two eigenvalues and eigenvectors. Compare with the results of section 5.3.
Assume that 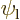 and
and 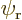 have been slightly adjusted to be orthonormal. Then so are
have been slightly adjusted to be orthonormal. Then so are 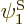 and
and 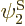 orthonormal, since the various six-dimensional inner product integrals, like
orthonormal, since the various six-dimensional inner product integrals, like
can according to the rules of calculus be factored into three-dimensional integrals as
which is zero if 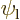 and
and 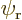 are orthonormal.
are orthonormal.
Also, do not try to find actual values for 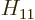 ,
, 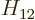 ,
, 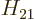 , and
, and 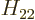 . As section 5.2 noted, that can only be done numerically. Instead just refer to
. As section 5.2 noted, that can only be done numerically. Instead just refer to 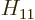 as
as 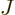 and to
and to 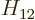 as
as 
 :
:
Next note that you also have
because they are the exact same inner product integrals; the difference is just which electron you number 1 and which one you number 2 that determines whether the wave functions are listed as 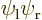 or
or 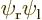 .
.
Solution matfor-a
-
2.
-
Find the eigenstates for the same problem, but now including spin.
As section 5.7 showed, the antisymmetric wave function with spin consists of a sum of six Slater determinants. Ignoring the highly excited first and sixth determinants that have the electrons around the same nucleus, the remaining 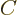
 4 Slater determinants can be written out explicitly to give the two-particle states
4 Slater determinants can be written out explicitly to give the two-particle states
Note that the Hamiltonian does not involve spin, to the approximation used in most of this book, so that, following the techniques of section 5.5, an inner product like 

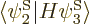 can be written out like
can be written out like
and then multiplied out into inner products of matching spin components to give
The other 15 matrix coefficients can be found similarly, and most will be zero.
If you do not have experience with linear algebra, you may want to skip this question, or better, just read the solution. However, the four eigenvectors are not that hard to guess; maybe easier to guess than correctly derive.
Solution matfor-b
![]() ,
,![]()
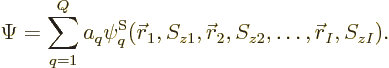
![]()
![]()
![]()
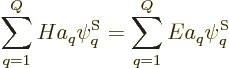
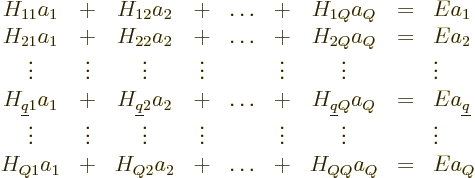
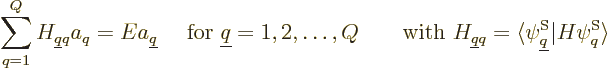
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()

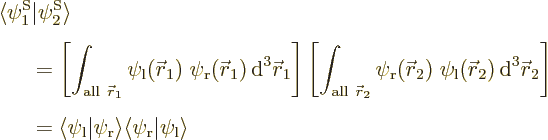
![]() ,
,![]() ,
,![]() ,
,![]() .
.![]()
![]()
![]()
![]()
![]() :
: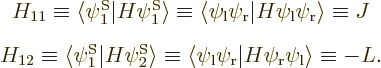
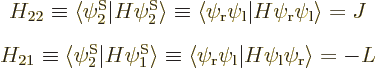
![]()
![]()
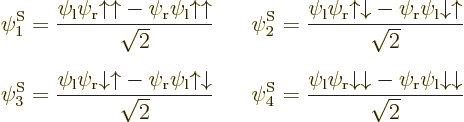
![]()
![]()
![]()