|
|
|
|
|
Next: 5.10 Pauli Repulsion |
|
This section solves the ground state electron configuration of the
atoms of elements heavier than hydrogen. The atoms of the elements
are distinguished by their “atomic number” ![]() ,
,![]()
A crude approximation will be made to deal with the mutual interactions between the electrons. Still, many properties of the elements can be understood using this crude model, such as their geometry and chemical properties, and how the Pauli exclusion principle raises the energy of the electrons.
This is a descriptive section, in which no new analytical procedures are taught. However, it is a very important section to read, and reread, because much of our qualitative understanding of nature is based on the ideas in this section.
The procedure to find the ground state of the heavier atoms is similar
to the one for the hydrogen atom of chapter 4.3. The total
energy Hamiltonian for the electrons of an element with atomic number
![]()
The Hamiltonian eigenvalue problem for the energy states takes the
form:
Key Points
- The Hamiltonian for the electron structure has been written down.
The Hamiltonian eigenvalue problem of the previous subsection cannot be solved exactly. The repulsive interactions between the electrons, given by the last term in the Hamiltonian are too complex.
More can be said under the, really poor, approximation that each
electron sees
a repulsion by the other ![]()
![]()
![]()
![]() .
.![]()
In this crude approximation, the electrons do not notice each other at
all; they see only a single charge hydrogen nucleus. Obviously
then, the wave function solutions for each electron should be the
![]()
To verify this explicitly, the approximate Hamiltonian is
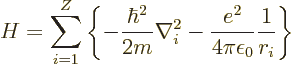
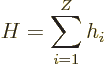
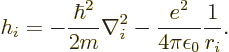
The approximate Hamiltonian eigenvalue problem can now be solved using
a method of separation of variables in which solutions are sought that
take the form of products of single-electron wave functions:

The first term in the equation above must be some constant
![]() ;
;![]()
![]()
![]()
The same observations hold for the other electrons; their
single-electron eigenfunctions are ![]()
![]()
![]()
![]() .
.
The final wave functions for all ![]()
![]()
This solves the Hamiltonian eigenvalue problem under the shielding
approximation. The bottom line is: just multiply ![]()
![]()
Key Points
- The Hamiltonian eigenvalue problem is too difficult to solve analytically.
- To simplify the problem, the detailed interactions between electrons are ignored. For each electron, it is assumed that the only effect of the other electrons is to cancel, or
shield,that many protons in the nucleus, leaving only a hydrogen nucleus strength.
- This is a very crude approximation.
- It implies that the
electron wave functions are products of the single-electron hydrogen atom wave functions. Their energy is the sum of the corresponding single-electron hydrogen energy levels. -
- These wave functions must still be combined together to satisfy the antisymmetrization requirement (Pauli exclusion principle).
This subsection starts off the discussion of the approximate ground
states of the elements. Atomic number ![]()
![]()
![]() ,
,1s
state, and the
single electron can be in the spin-up or spin-down versions of that
state, or in any combination of the two. The most general ground
state wave function is therefore:
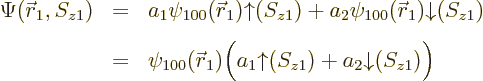
ionization energythat would be needed to remove the electron from the atom is the absolute value of the energy eigenvalue
For helium, with ![]()
![]()
![]() .
.![]()
![]()
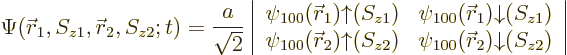 |
(5.35) |

Figure 5.4 shows the approximate probability density for the first two elements, indicating where electrons are most likely to be found. In reality, the shielding approximation underestimates the nuclear attraction and the shown helium atom is much too big.
It is good to remember that the ![]()
![]()
The analysis predicts that the ionization energy to remove one electron from helium would be 13.6 eV, the same as for the hydrogen atom. This is a very bad approximation indeed; the truth is almost double, 24.6 eV.
The problem is the made assumption that the repulsion by the other
electron shields
one of the two protons in the helium
nucleus, so that only a single-proton hydrogen nucleus is seen. When
electron wave functions overlap significantly as they do here, their
mutual repulsion is a lot less than you would naively expect, (compare
figure 13.7). As a result, the second proton is only
partly shielded, and the electron is held much more tightly than the
analysis predicts. See addendum {A.38.2} for better
estimates of the helium atom size and ionization energy.
However, despite the inaccuracy of the approximation chosen, it is probably best to stay consistent, and not fool around at random. It must just be accepted that the theoretical energy levels will be too small in magnitude {N.7}.
The large ionization energy of helium is one reason that it is chemically inert. Helium is called a “noble” gas, presumably because nobody expects nobility to do anything.
Key Points
- The ground states of the atoms of the elements are to be discussed.
- Element one is hydrogen, solved before. Its ground state is
with arbitrary spin. Its ionization energy is 13.6 eV.
- Element two is helium. Its ground state has both electrons in the lowest-energy spatial state
and locked into the singlet spin state. Its ionization energy is 24.6 eV. ,
- The large ionization energy of helium means it holds onto its two electrons tightly. Helium is an inert noble gas.
- The two
1sstatesand are called the K shell.
The next element is lithium, with three electrons. This is the first
element for which the antisymmetrization requirement forces the
theoretical energy to go above the hydrogen ground state level
![]() .
.![]()
![]() .
.![]()
![]()
This effect of the antisymmetrization requirement, that a new state
must become occupied
every time an electron is added
is known as the Pauli exclusion principle. It causes the energy values to become
larger and larger as the supply of low energy states runs out.
The transition to the higher energy level ![]()
 |
For the third electron of the lithium atom, the available states with
theoretical energy ![]()
![]()
2s
states and the ![]() ,
,![]() ,
,![]()
2p
states, a total of eight possible
states. These states are, of course, commonly called the “L
shell.”
Within the crude nuclear shielding approximation made, all eight states have the same energy. However, on closer examination, the spherically symmetric 2s states really have less energy than the 2p ones. Very close to the nucleus, shielding is not a factor and the full attractive nuclear force is felt. So a state in which the electron is more likely to be close to the nucleus has less energy. Those are the 2s states; in the 2p states, which have nonzero orbital angular momentum, the electron tends to stay away from the immediate vicinity of the nucleus {N.8}.
Within the assumptions made, there is no preference with regard to the
spin direction of the 2s state, allowing two Slater determinants to be
formed.
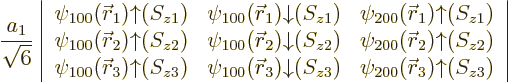 | |||||
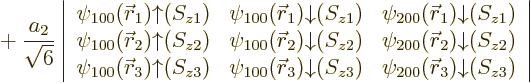 | (5.36) |
It is common to say that the “third electron goes into a
![]() ”
”![]()
owns
the state. For
the same reason, the Pauli exclusion principle is commonly phrased as “no two
electrons may occupy the same state”, even though the Slater
determinants imply that all electrons share all states equally.
Since the third electron is bound with the much lower energy ![]()
![]() ,
,![]()
![]()
Lithium will readily give up its loosely bound third electron in chemical reactions. Conversely, helium would have even less hold on a third electron than lithium, because it has only two protons in its nucleus. Helium simply does not have what it takes to seduce an electron away from another atom. This is the second part of the reason that helium is chemically inert: it neither will give up its electrons nor take on additional ones.
Thus the Pauli exclusion principle causes different elements to behave chemically in very different ways. Even elements that are just one unit apart in atomic number such as helium (inert) and lithium (very active).
For beryllium, with four electrons, the same four states as for
lithium combine in a single ![]()
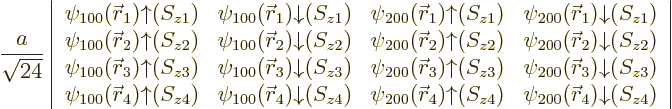 |
(5.37) |
For boron, one of the ![]()
2p
states will need
to be occupied. Within the approximations made, there is no
preference for any particular state. As an example, figure
5.7 shows the approximate solution in which the
![]() ,
,2
state is
occupied. It may be recalled from figure 4.11 that this
state remains close to the ![]()
![]() -
-
The ionization energy decreases a bit to 8.3 eV, indicating that indeed the 2p states have higher energy than the 2s ones.
For carbon, a second ![]()
![]()
![]()
![]() -
-![]()
![]() -
-![]() -
-![]()
![]()
For nitrogen, the third 2p electron can go into the 2![]()
![]() -
-
However, for oxygen the game is up. There are no more free spatial
states in the L shell. The new electron will have to go, say, into
the ![]()
For fluorine, the next electron goes into the 2![]()
![]()
For neon, all 2p electrons are paired, and the L shell is full. This
makes neon an inert noble gas like helium: it cannot accommodate any
more electrons at the ![]()
On the other hand, the previous element, fluorine, has a nucleus that
is almost as strong, and it can accommodate an additional electron in
its unpaired 2![]()
Neighboring elements oxygen and nitrogen are less electronegative, but oxygen can accommodate two additional electrons rather than one, and nitrogen will even accommodate three.
Key Points
- The Pauli exclusion principle forces states of higher energy to become occupied when the number of electrons increases. This raises the energy levels greatly above what they would be otherwise.
- With the third element, lithium, one of the
- Conversely, helium will not take on a third electron.
- The fourth element is beryllium, with both 2s states occupied.
- For boron, carbon, nitrogen, oxygen, fluorine, and neon, the successive
- Neon is a noble gas like helium: it holds onto its electrons tightly, and will not accommodate any additional electrons since they would have to enter the
energy level states.
- Fluorine, oxygen, and nitrogen, however, are very willing to accommodate additional electrons in their vacant 2p states.
- The eight states
are called the “L shell.”
Starting with sodium (natrium), the ![]() ,
,valence
of one; they
are willing to sacrifice one electron.
Similarly, the elements following sodium in the third row of the periodic figure 5.5 mirror the corresponding elements in the previous row. Near the end of the row, the elements are again eager to accept additional electrons in the still vacant 3p states.
Finally argon, with no 3s and 3p vacancies left, is again inert. This
is actually somewhat of a surprise, because the ![]()
![]()
3d
states. (What
else?) According to the approximations made, the 3s, 3p, and 3d
states would all have the same energy. So it might seem that argon
could accept additional electrons into the 3d states.
But it was already noted that the p states in reality have more energy than the s states at the same theoretical energy level, and the d states have even more. The reason is the same: the d states stay even further away from the nucleus than the p states. Because of the higher energy of the d states, argon is really not willing to accept additional electrons.
Key Points
- The next eight elements mirror the properties of the previous eight, from the metal sodium to the highly electronegative chlorine and the noble gas argon.
- The states
are called the “M shell.”
The logical continuation of the story so far would be that the potassium (kalium) atom would be the first one to put an electron into a 3d state. However, by now the shielding approximation starts to fail not just quantitatively, but qualitatively. The 3d states actually have so much more energy than the 3s states that they even exceed the energy of the 4s states. Potassium puts its last electron into a 4s state, not a 3d one. This makes its outer shell much like the ones of lithium and sodium, so it starts a new row in the periodic table.
The next element, calcium, fills the 4s shell, putting an end to that game. Since the six 4p states have more energy, the next ten elements now start filling the skipped 3d states with electrons, leaving the N-shell with 2 electrons in it. (Actually, this is not quite precise; the 3d and 4s energies are closely together, and for chromium and copper one of the two 4s electrons turns out to switch to a 3d state.) In any case, it takes until gallium until the six 4p states start filling, which is fully accomplished at krypton. Krypton is again a noble gas, though it can form a weak bond with chlorine.
Continuing to still heavier elements, the energy levels get even more confused. This discussion will stop while it is still ahead.
Key Points
- Unlike what the approximate theory says, in real life the 4s states
have less energy than the 3d states, and are filled first.
- After that, the transition metals fill the skipped 3d states before the old logic resumes.
- The states
are called the “N shell.” It all spells KLM Netherlands.
- The substates are of course called
s,p,”...d,“f,
A complete periodic table of the elements is shown in figure
5.8. The number in the top left corner of each cell is the
atomic number ![]()
![]()
![]()
![]()
![]()
![]()
![]()
 |
The top part of the shown table is called the main group. For some reason however, hydrogen is not included in this term. Note that compared to the previous abbreviated periodic table, hydrogen and helium have been moved to the final columns. The idea is to combine elements with similar properties together into the same columns. Helium is a noble gas like the group VIII elements with filled electron shells. Helium has absolutely nothing in common with the group II alkaline metals that have two electrons in an otherwise empty shell. Similarly, hydrogen behaves much more like a halogen with 1 electron missing from a filled shell than like an alkali metal with 1 electron in an otherwise empty shell. However, hydrogen is still sufficiently different that it should not be considered an actual halogen.
The elements in the periodic table are classified as metals, metalloids, and nonmetals. Metalloids have chemical properties intermediate between metals and nonmetals. The band of metalloids is indicated by dark red cell boundaries in figure 5.8. It extends from boron to polonium. The metals are found to the left of this band and the nonmetals to the right. Hydrogen and helium are most definitely nonmetals and their shown position in the table reflects that.
The color of each cell indicates the ionization energy, increasing from bluish to reddish. The length of the bar below the atomic number gives the electronegativity. In the top right corner wavy lines indicate that the element is a liquid under normal conditions, and dots that it is a gas. A dagger indicates that the atomic nucleus is radioactive (for every isotope, chapter 14). If the dagger is followed by an exclamation mark, the radioactivity causes the nucleus to decay fast enough that there are no usable quantities of the element found in nature. These elements must be artificially prepared in a lab.
The boxes below the element names indicate the s, p, d, and f shells
being filled in that period of the table. The shells already filled
in the noble gas at the end of the previous period remain filled and
are not shown. Note that the filling of ![]() d
d![]() ,
,![]() f
f![]() .
.
Besides element name, symbol, and radioactivity, periodic table figure 5.8 limits itself to data for which the periodic table arrangement is meaningful. Many other periodic tables also list the average atomic mass for the isotopic composition found on earth. However, for purposes of understanding atomic masses physically, graphs in chapter 14 on nuclei, like figures 14.2 and 14.4, are much more useful.
It should be noted that periodic table figure 5.8 deviates in a number of aspects from the normal conventions. Figure 5.8 is what seems the simplest and most logical. If you put historical oddities and a few committees in charge, you get something different.
Most prominently, most periodic tables leave hydrogen in group I instead of moving it to the top of group VII. But if you move helium to group VIII because of its similarity with the other noble gases in that group, then it is ludicrous to leave hydrogen in group I. Hydrogen has virtually nothing in common with the alkali metals in group I. Like the light halogens, it is a diatomic gas under normal conditions, not a solid metal. Even at the extremely low temperatures at which hydrogen solidifies, it is a nonconducting molecular solid, not a metal. The melting, boiling, and critical points of hydrogen form a logical sequence with those of the halogens. They are totally inconsistent with those of the alkali metals. Hydrogen has the ionization energy of oxygen and the electronegativity of phosphorus. A ionic compound like NaH is a direct equivalent of NaCl, salt, with the hydrogen as the negative ion.
It is true that hydrogen can also form positive ions in chemical
reactions, more or less, something that the halogens simply do not do.
But do not actually expect to find bare protons when other atoms are
around. Also the ionization energy and electronegativity of hydrogen
are quite a bit out of line with those of the other halogens.
Hydrogen is certainly not a true halogen. But if you order the
elements by properties, there is no doubt that hydrogen belongs in
group VII, not I. If you want to refer to the quantum-mechanical
shell structure, the term s block
can still be used to
indicate the alkali and alkaline metals along with hydrogen and
helium. The remainder of the main group is the
p block.
These names indicate the quantum states being
filled.
The term transition metals may not include the elements in group IIB of the d-block, for reason related to the fact that their s and d shells have been completely filled. The f-block elements are sometimes referred to as the inner transition metals.
Further, according to the 2005 IUPAC Red Book the lanthanides and
actinides should be more properly called the lanthanoids and
actinoids, since ide
usually means negative ion.
Since oid” means “-like,
according to
IUPAC the lanthanoids should not really include lanthanum, and the
actinoids should not include actinium. However, the IUPAC does
include them because of common usage. A rare triumph of scientific
common sense over lousy terminology. If lanthanum and actinium are to
be included, the lanthanides and actinides should of course simply
have been renamed the lanthanum and actinium groups, or equivalent,
not lanthanoids and actinoids.
More significantly, unlike figure 5.8 suggests, lutetium is included in the lanthanoids and lawrencium in the actinoids. The term rare-earth metals include the lanthanoids, as well as scandium and yttrium as found immediately above lutetium.
Also, both lutetium and lawrencium are according to IUPAC included in the f-block. That makes the f-block 15 columns wide instead of the 14 column block shown at the bottom of figure 5.8. Of course, that does not make any sense at all. The name f-block supposedly indicates that an f-shell is being filled. An f-shell holds 14 electrons, not 15. For lutetium, the f-shell is full and other shells have begun to fill. The same is, at the time of writing, believed to be true for lawrencium. And while the first f-shell electrons for lanthanum and actinium get temporarily bumped to the d-shell, that is obviously a minor error in the overall logic of filling the f-shell. (Apparently, there is a long-standing controversy whether lanthanum and actinium or lutetium and lawrencium should be included in the f-block. By compromising and putting both in the f-block of their 2007 periodic table, the IUPAC got the worst of both worlds.)
A nice recent example of a more conventional periodic table by an authoritative source is from NIST. This also includes the latest updates on various data, unlike the periodic table in this book. An earlier version can be found at the web location of this document. The hieroglyphs found in the NIST table are explained in chapter 10.7.1.
Periodic table figure 5.8 was based on data from various
sources. Shell fillings and ionization energies agree with the NIST
listing and table. The uncertain shell fillings at atomic numbers 103
and 104 were left out. The classification whether the elements must
be artificially prepared was taken from the NIST periodic table. The
electronegativities are based on the Pauling scale. They were taken
from Wikipedia use
values, that were in turn taken
from WebElements, and are mostly the same as those in the 2003 CRC
Handbook of Chemistry and Physics, and the 1999 Lange’s Handbook
of Chemistry. Discrepancies between these sources of more than 10%
occur for atomic numbers 71, 74, 82, and 92.