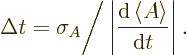| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
A.18 The energy-time uncertainty relationship
As mentioned in chapter 4.5.3, Heisenberg’s formulae
relating the typical uncertainties in momentum and position is often
very convenient for qualitative descriptions of quantum mechanics,
especially if you misread 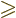 as
as 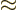 .
.
So, taking a cue from relativity, people would like to write a similar
expression for the uncertainty in the time coordinate,
The energy uncertainty can reasonably be defined as the standard
deviation 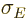 in energy. However, if you want to formally
justify the energy-time relationship, it is not at all obvious what to
make of that uncertainty in time
in energy. However, if you want to formally
justify the energy-time relationship, it is not at all obvious what to
make of that uncertainty in time 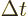 .
.
To arrive at one definition, assume that the variable of real interest
in a given problem has a time-invariant operator  . The
generalized uncertainty relationship of chapter 4.5.2
between the uncertainties in energy and
. The
generalized uncertainty relationship of chapter 4.5.2
between the uncertainties in energy and  is then:
is then:
But according to chapter 7.2 ![$\vert\langle[H,A]\rangle\vert$](img4183.gif) is
just
is
just 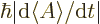 .
.
So the Mandelshtam-Tamm version of the energy-time uncertainty
relationship just defines the uncertainty in time to be
That corresponds to the typical time in which the expectation value of
 changes by one standard deviation. In other words, it is the time
that it takes for
changes by one standard deviation. In other words, it is the time
that it takes for  to change to a value sufficiently different that
it will clearly show up in measurements.
to change to a value sufficiently different that
it will clearly show up in measurements.
![]() .
.![]()