| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
Subsections
4.5 The Commutator
As the previous section discussed, the standard deviation  is
a measure of the uncertainty of a property of a quantum system. The
larger the standard deviation, the farther typical measurements stray
from the expected average value. Quantum mechanics often requires a
minimum amount of uncertainty when more than one quantity is involved,
like position and linear momentum in Heisenberg's uncertainty
principle. In general, this amount of uncertainty is related to an
important mathematical object called the
is
a measure of the uncertainty of a property of a quantum system. The
larger the standard deviation, the farther typical measurements stray
from the expected average value. Quantum mechanics often requires a
minimum amount of uncertainty when more than one quantity is involved,
like position and linear momentum in Heisenberg's uncertainty
principle. In general, this amount of uncertainty is related to an
important mathematical object called the commutator
,
to be discussed in this section.
4.5.1 Commuting operators
First, note that there is no fundamental reason why several quantities
cannot have a definite value at the same time. For example, if
the electron of the hydrogen atom is in a 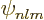 eigenstate, its
total energy, square angular momentum, and
eigenstate, its
total energy, square angular momentum, and  -component of angular
momentum all have definite values, with zero uncertainty.
-component of angular
momentum all have definite values, with zero uncertainty.
More generally, two different quantities with operators  and
and  have definite values if the wave function is an eigenfunction of both
have definite values if the wave function is an eigenfunction of both
 and
and  . So, the question whether two quantities can be
definite at the same time is really whether their operators
. So, the question whether two quantities can be
definite at the same time is really whether their operators  and
and
 have common eigenfunctions. And it turns out that the answer has
to do with whether these operators “commute”, in other words, on whether their order can be
reversed as in
have common eigenfunctions. And it turns out that the answer has
to do with whether these operators “commute”, in other words, on whether their order can be
reversed as in 

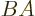 .
.
In particular, {D.18}:
Iff two Hermitian operators commute, there is a complete set of
eigenfunctions that is common to them both.
(For more than two operators, each operator has to commute with all
others.)
For example, the operators 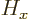 and
and 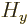 of the harmonic oscillator
of chapter 4.1.2 commute:
of the harmonic oscillator
of chapter 4.1.2 commute:
This is true since it makes no difference whether you differentiate
 first with respect to
first with respect to  and then with respect to
and then with respect to  or vice
versa, and since the
or vice
versa, and since the 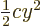 can be pulled in front of the
can be pulled in front of the
 -differentiations and the
-differentiations and the  can be pushed inside
the
can be pushed inside
the  -differentiations, and since multiplications can always
be done in any order.
-differentiations, and since multiplications can always
be done in any order.
The same way, 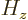 commutes with
commutes with 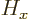 and
and 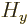 , and that
means that
, and that
means that 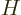 commutes with them all, since
commutes with them all, since 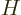 is just their sum.
So, these four operators should have a common set of eigenfunctions,
and they do: it is the set of eigenfunctions
is just their sum.
So, these four operators should have a common set of eigenfunctions,
and they do: it is the set of eigenfunctions 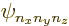 derived in chapter 4.1.2.
derived in chapter 4.1.2.
Similarly, for the hydrogen atom, the total energy Hamiltonian
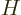 , the square angular momentum operator
, the square angular momentum operator 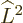 and the
and the
 -component of angular momentum
-component of angular momentum  all commute, and they have
the common set of eigenfunctions
all commute, and they have
the common set of eigenfunctions 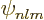 .
.
Note that such eigenfunctions are not necessarily the only game in
town. As a counter-example, for the hydrogen atom 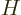 ,
,
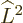 , and the
, and the  -component of angular momentum
-component of angular momentum 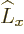 also all commute, and they too have a common set of eigenfunctions.
But that will not be the
also all commute, and they too have a common set of eigenfunctions.
But that will not be the 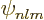 , since
, since 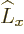 and
and
 do not commute. (It will however be the
do not commute. (It will however be the 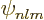 after you
rotate them all 90 degrees around the
after you
rotate them all 90 degrees around the  -axis.) It would
certainly be simpler mathematically if each operator had just one
unique set of eigenfunctions, but nature does not cooperate.
-axis.) It would
certainly be simpler mathematically if each operator had just one
unique set of eigenfunctions, but nature does not cooperate.
Key Points

- Operators commute if you can change their order, as in


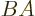 .
.

- For commuting operators, a common set of eigenfunctions exists.

- For those eigenfunctions, the physical quantities corresponding
to the commuting operators all have definite values at the same
time.
4.5.1 Review Questions
-
1.
-
The pointer state
is one of the eigenstates that 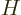 ,
, 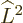 , and
, and 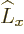 have in common. Check that it is not an eigenstate that
have in common. Check that it is not an eigenstate that 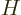 ,
, 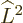 , and
, and  have in common.
have in common.
Solution commutea-a
4.5.2 Noncommuting operators and their commutator
Two quantities with operators that do not commute cannot in general
have definite values at the same time. If one has a definite
value, the other is in general uncertain.
The qualification in general
is needed because there
may be exceptions. The angular momentum operators do not commute, but
it is still possible for the angular momentum to be zero in all three
directions. But as soon as the angular momentum in any direction is
nonzero, only one component of angular momentum can have a definite
value.
A measure for the amount to which two operators  and
and  do not
commute is the difference between
do not
commute is the difference between  and
and 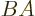 ; this difference
is called their “commutator”
; this difference
is called their “commutator” ![$[A,B]$](img786.gif) :
:
![\begin{displaymath}
\fbox{$\displaystyle [A,B] \equiv A B - B A $}
\end{displaymath}](img787.gif) |
(4.45) |
A nonzero commutator ![$[A,B]$](img786.gif) demands a minimum amount of uncertainty
in the corresponding quantities
demands a minimum amount of uncertainty
in the corresponding quantities  and
and 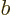 . It can be shown,
{D.19}, that the uncertainties, or standard
deviations,
. It can be shown,
{D.19}, that the uncertainties, or standard
deviations, 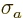 in
in  and
and 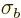 in
in 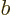 are at least so
large that:
are at least so
large that:
![\begin{displaymath}
\fbox{$\displaystyle
\sigma_a \sigma_b \mathrel{\raisebox{...
...$}}{\textstyle\frac{1}{2}} \vert\langle[A,B]\rangle\vert
$} %
\end{displaymath}](img789.gif) |
(4.46) |
This equation is called the “generalized uncertainty relationship”.
Key Points

- The commutator of two operators
 and
and  equals
equals  and
is written as
and
is written as ![$[A,B]$](img786.gif) .
.

- The product of the uncertainties in two quantities is at least
one half the magnitude of the expectation value of their commutator.
4.5.3 The Heisenberg uncertainty relationship
This section will work out the uncertainty relationship (4.46)
of the previous subsection for the position and linear momentum in an
arbitrary direction. The result will be a precise mathematical
statement of the Heisenberg uncertainty principle.
To be specific, the arbitrary direction will be taken as the  -axis,
so the position operator will be
-axis,
so the position operator will be  , and the linear momentum
operator
, and the linear momentum
operator 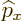



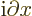 . These
two operators do not commute,
. These
two operators do not commute,  is simply not the same as
is simply not the same as
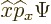 :
:  means multiply function
means multiply function  by
by  to get the product function
to get the product function  and then apply
and then apply 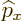 on that
product, while
on that
product, while 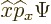 means apply
means apply 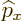 on
on  and then
multiply the resulting function by
and then
multiply the resulting function by  . The difference is found
from writing it out:
. The difference is found
from writing it out:
the second equality resulting from differentiating out the product.
Comparing start and end shows that the difference between 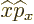 and
and
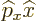 is not zero, but
is not zero, but 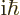 . By definition, this
difference is their commutator:
. By definition, this
difference is their commutator:
![\begin{displaymath}
\fbox{$\displaystyle [{\widehat x},{\widehat p}_x] = {\rm i}\hbar $} %
\end{displaymath}](img797.gif) |
(4.47) |
This important result is called the “canonical commutation relation.” The commutator of position and linear momentum in
the same direction is the nonzero constant 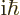 .
.
Because the commutator is nonzero, there must be nonzero uncertainty
involved. Indeed, the generalized uncertainty relationship of the
previous subsection becomes in this case:
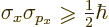 |
(4.48) |
This is the uncertainty relationship as first formulated by Heisenberg.
It implies that when the uncertainty in position 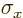 is
narrowed down to zero, the uncertainty in momentum
is
narrowed down to zero, the uncertainty in momentum 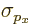 must
become infinite to keep their product nonzero, and vice versa. More
generally, you can narrow down the position of a particle and you can
narrow down its momentum. But you can never reduce the product of the
uncertainties
must
become infinite to keep their product nonzero, and vice versa. More
generally, you can narrow down the position of a particle and you can
narrow down its momentum. But you can never reduce the product of the
uncertainties 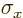 and
and 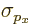 below
below
 , whatever you do.
, whatever you do.
It should be noted that the uncertainty relationship is often written
as 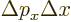
 or even as
or even as
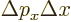
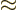
 where
where 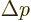 and
and
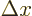 are taken to be vaguely described
are taken to be vaguely described
uncertainties
in momentum and position, rather than
rigorously defined standard deviations. And people write a
corresponding uncertainty relationship for time, 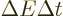
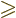
 , because relativity suggests that time
should be treated just like space. But note that unlike the linear
momentum operator, the Hamiltonian is not at all universal. So, you
might guess that the definition of the
, because relativity suggests that time
should be treated just like space. But note that unlike the linear
momentum operator, the Hamiltonian is not at all universal. So, you
might guess that the definition of the uncertainty
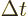 in time would not be universal either, and you would be
right, chapter 7.2.2.
in time would not be universal either, and you would be
right, chapter 7.2.2.
Key Points

- The canonical commutator
![$[{\widehat x},{\widehat p}_x]$](img808.gif) equals
equals 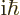 .
.

- If either the uncertainty in position in a given direction or
the uncertainty in linear momentum in that direction is narrowed
down to zero, the other uncertainty blows up.

- The product of the two uncertainties is at least the constant
 .
.
4.5.3 Review Questions
-
1.
-
This sounds serious! If I am driving my car, the police requires me to know my speed (linear momentum). Also, I would like to know where I am. But neither is possible according to quantum mechanics.
Solution commutec-a
4.5.4 Commutator reference
It is a fact of life in quantum mechanics that commutators pop up all
over the place. Not just in uncertainty relations, but also in the
time evolution of expectation values, in angular momentum, and in
quantum field theory, the advanced theory of quantum mechanics used in
solids and relativistic applications. This section can make your life
easier dealing with them. Browse through it to see what is there.
Then come back when you need it.
Recall the definition of the commutator ![$[A,B]$](img786.gif) of any two operators
of any two operators
 and
and  :
:
![\begin{displaymath}[A,B]= AB - BA %
\end{displaymath}](img809.gif) |
(4.49) |
By this very definition , the commutator is zero for any two operators 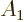 and
and 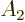 that commute, (whose order can be interchanged):
that commute, (whose order can be interchanged):
![\begin{displaymath}[A_1,A_2]= 0 \quad
\mbox{if $A_1$\ and $A_2$\ commute; } A_1 A_2 = A_2 A_1. %
\end{displaymath}](img812.gif) |
(4.50) |
If operators all commute, all their products commute too:
![\begin{displaymath}[A_1 A_2 \ldots A_k, A_{k+1}\ldots A_n]= 0
\quad \mbox{if } ...
... A_2, \ldots, A_k, A_{k+1},\ldots, A_n
\mbox{ all commute.} %
\end{displaymath}](img813.gif) |
(4.51) |
Everything commutes with itself, of course:
![\begin{displaymath}[A,A]= 0, %
\end{displaymath}](img814.gif) |
(4.52) |
and everything commutes with a numerical constant; if  is an
operator and
is an
operator and  is some number, then:
is some number, then:
![\begin{displaymath}[A,a]= [a,A] = 0. %
\end{displaymath}](img815.gif) |
(4.53) |
The commutator is antisymmetric
; or in simpler words,
if you interchange the sides; it will change the sign,
{D.20}:
![\begin{displaymath}[B,A]= - [A,B]. %
\end{displaymath}](img816.gif) |
(4.54) |
For the rest however, linear combinations multiply out just like you
would expect:
![\begin{displaymath}[aA+bB,cC+dD]=
ac[A,C] + ad[A,D] + bc[B,C] + bd[B,D], %
\end{displaymath}](img817.gif) |
(4.55) |
(in which it is assumed that  ,
,  ,
, 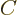 , and
, and  are operators, and
are operators, and  ,
, 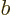 ,
,  , and
, and 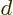 numerical
constants.)
numerical
constants.)
To deal with commutators that involve products of operators, the
rule to remember is: “the first factor comes out at the front
of the commutator, the second at the back”. More precisely:
![\begin{displaymath}
\rule[-10pt]{7pt}{0pt}
\raisebox{-7pt}{
\begin{picture}(0...
...}}
\end{picture} }
[\ldots,AB] = A[\ldots,B] + [\ldots,A]B. %
\end{displaymath}](img821.gif) |
(4.56) |
So, if  or
or  commutes with the other side of the operator, it
can simply be taken out at at its side; (the second commutator will be
zero.) For example,
commutes with the other side of the operator, it
can simply be taken out at at its side; (the second commutator will be
zero.) For example,
if 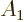 and
and 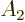 commute.
commute.
Now from the general to the specific. Because changing sides in a
commutator merely changes its sign, from here on only one of the two
possibilities will be shown. First the position operators all
mutually commute:
![\begin{displaymath}[{\widehat x},{\widehat y}]=[{\widehat y},{\widehat z}]=[{\widehat z},{\widehat x}]=0 %
\end{displaymath}](img823.gif) |
(4.57) |
as do position-dependent operators such as a potential energy
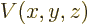 :
:
![\begin{displaymath}[{\widehat x},V(x,y,z)]=[{\widehat y},V(x,y,z)]=[{\widehat z},V(x,y,z)]=0 %
\end{displaymath}](img825.gif) |
(4.58) |
This illustrates that if a set of operators all commute, then all
combinations of those operators commute too.
The linear momentum operators all mutually commute:
![\begin{displaymath}[{\widehat p}_x,{\widehat p}_y]=
[{\widehat p}_y,{\widehat p}_z] =
[{\widehat p}_z,{\widehat p}_x] = 0 %
\end{displaymath}](img826.gif) |
(4.59) |
However, position operators and linear momentum operators in the same
direction do not commute; instead:
![\begin{displaymath}[{\widehat x},{\widehat p}_x]=
[{\widehat y},{\widehat p}_y] =
[{\widehat z},{\widehat p}_z] = {\rm i}\hbar %
\end{displaymath}](img827.gif) |
(4.60) |
As seen in the previous subsection, this lack of commutation causes
the Heisenberg uncertainty principle. Position and linear momentum
operators in different directions do commute:
![\begin{displaymath}[{\widehat x},{\widehat p}_y]=
[{\widehat x},{\widehat p}_z]...
...ehat z},{\widehat p}_x] =
[{\widehat z},{\widehat p}_y] = 0 %
\end{displaymath}](img828.gif) |
(4.61) |
A generalization that is frequently very helpful is:
![\begin{displaymath}[f,{\widehat p}_x]= {\rm i}\hbar \frac{\partial f}{\partial x...
...{\widehat p}_z] = {\rm i}\hbar \frac{\partial f}{\partial z} %
\end{displaymath}](img829.gif) |
(4.62) |
where  is any function of
is any function of  ,
,  , and
, and  .
.
Unlike linear momentum operators, angular momentum operators do
not mutually commute. The commutators are given by the
so-called “
fundamental commutation relations:”
![\begin{displaymath}[\L _x,\L _y]= {\rm i}\hbar\L _z \quad
[\L _y,\L _z] = {\rm i}\hbar\L _x \quad
[\L _z,\L _x] = {\rm i}\hbar\L _y %
\end{displaymath}](img830.gif) |
(4.63) |
Note the  order of the indices that produces
positive signs; a reversed
order of the indices that produces
positive signs; a reversed 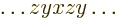 order adds a minus
sign. For example
order adds a minus
sign. For example ![$[\L _z,\L _y]$](img833.gif)

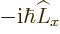 because
because  following
following
 is in reversed order.
is in reversed order.
The angular momentum components do all commute with the square angular
momentum operator:
![\begin{displaymath}[\L _x,\L ^2]= [\L _y,\L ^2] = [\L _z,\L ^2] = 0
\quad\mbox{where } \L ^2 = \L _x^2 + \L _y^2 + \L _z^2 %
\end{displaymath}](img835.gif) |
(4.64) |
Just the opposite of the situation for linear momentum, position and
angular momentum operators in the same direction commute,
![\begin{displaymath}[{\widehat x}, \L _x]= [{\widehat y}, \L _y] = [{\widehat z}, \L _z] = 0 %
\end{displaymath}](img836.gif) |
(4.65) |
but those in different directions do not:
![\begin{displaymath}[{\widehat x},\L _y]=[\L _x,{\widehat y}]={\rm i}\hbar {\wide...
...hat z},\L _x]=[\L _z,{\widehat x}]={\rm i}\hbar {\widehat y} %
\end{displaymath}](img837.gif) |
(4.66) |
Square position commutes with all components of angular momentum,
![\begin{displaymath}[{\widehat r}^2,\L _x]= [{\widehat r}^2,\L _y] = [{\widehat r}^2,\L _z]
= [{\widehat r}^2,\L ^2] = 0 %
\end{displaymath}](img838.gif) |
(4.67) |
The commutator between position and square angular momentum is,
using vector notation for conciseness,
![\begin{displaymath}[{\skew 2\widehat{\skew{-1}\vec r}},\L ^2]= - 2\hbar^2 {\skew...
...t{\skew{-1}\vec r}}\cdot{\skew 4\widehat{\skew{-.5}\vec p}}) %
\end{displaymath}](img839.gif) |
(4.68) |
The commutators between linear and angular momentum are very similar
to the ones between position and angular momentum:
![\begin{displaymath}[{\widehat p}_x, \L _x]= [{\widehat p}_y, \L _y] = [{\widehat p}_z, \L _z] = 0 %
\end{displaymath}](img840.gif) |
(4.69) |
![\begin{displaymath}[{\widehat p}_x,\L _y]=[\L _x,{\widehat p}_y]={\rm i}\hbar {\...
..._z,\L _x]=[\L _z,{\widehat p}_x]={\rm i}\hbar {\widehat p}_y %
\end{displaymath}](img841.gif) |
(4.70) |
![\begin{displaymath}[{\widehat p}^2,\L _x]= [{\widehat p}^2,\L _y] = [{\widehat p}^2,\L _z]
= [{\widehat p}^2,\L ^2] = 0 %
\end{displaymath}](img842.gif) |
(4.71) |
![\begin{displaymath}[{\skew 4\widehat{\skew{-.5}\vec p}},\L ^2]= - 2\hbar^2 {\ske...
...{\skew{-.5}\vec p}}\cdot{\skew 4\widehat{\skew{-.5}\vec p}}) %
\end{displaymath}](img843.gif) |
(4.72) |
The following commutators are also useful:
![\begin{displaymath}[{\skew0\vec r}\times{\skew 4\widehat{\vec L}},\L ^2]= 2 {\rm...
...],\L ^2] = 2\hbar^2({\skew0\vec r}\L ^2+\L ^2{\skew0\vec r}) %
\end{displaymath}](img844.gif) |
(4.73) |
Commutators involving spin are discussed in a later chapter,
5.5.3.
Key Points

- Rules for evaluating commutators were given.

- Return to this subsection if you need to figure out some
commutator or the other.
![]()
![]()
![]() -
-![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
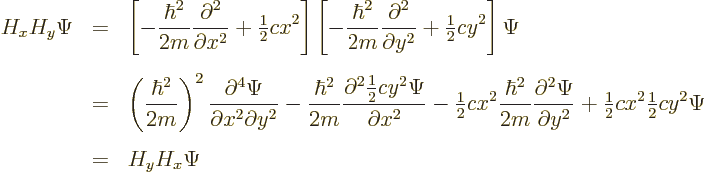
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]() ,
,![]()
![]() -
-![]()
![]() .
.![]() ,
,![]() ,
,![]() -
-![]()
![]() ,
,![]()
![]()
![]()
![]() -
-.
![]()
![]()
![]()
![]() ;
;![]() :
:![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
.
![]() -
-![]() ,
,![]()
![]()
![]()
![]()
![]() .
.![]()
![]() :
:![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
.
.
![]()
![]()
![]() :
: