| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
A.17 The virial theorem
The virial theorem relates the expectation kinetic energy of a quantum
system to the potential. That is of theoretical interest, as well as
important for computational methods like “density functional
theory.”
Consider a quantum system in a state of definite energy  . In
other words, consider a quantum system in a stationary state. It does
not have to be the ground state. The quantum system will be assumed to
be in infinite space.
. In
other words, consider a quantum system in a stationary state. It does
not have to be the ground state. The quantum system will be assumed to
be in infinite space.
To keep it simple, for now assume that there is a single particle with
position vector  in a potential
in a potential 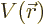 . That covers our
previous examples of the harmonic oscillator and the hydrogen atom.
. That covers our
previous examples of the harmonic oscillator and the hydrogen atom.
Then the virial theorem relates the expectation kinetic energy
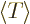 to the potential
to the potential  as follows:
as follows:
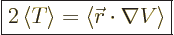 |
(A.75) |
(Recall that nabla,  , is just the multi-dimensional derivative
, is just the multi-dimensional derivative
 .) The above formula can be very useful.
.) The above formula can be very useful.
For example, consider the harmonic oscillator. There
so in Cartesian coordinates
Then according to the virial theorem 

 . So
the expectation kinetic energy and the expectation potential energy
are the same. Compute whichever is easiest, or just take half of the
total energy
. So
the expectation kinetic energy and the expectation potential energy
are the same. Compute whichever is easiest, or just take half of the
total energy  if you know it.
if you know it.
Also consider the hydrogen atom. There
so in polar coordinates
Then according to the virial theorem the expectation potential energy
is minus twice the expectation kinetic energy. And their sum, the
total energy  , is then minus the expectation kinetic energy. In
short,
, is then minus the expectation kinetic energy. In
short, 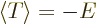 and
and  with
with  negative.
negative.
The virial theorem does not apply to the particle in a pipe, as that
particle is in a bounded space. (You can assume infinite space if
you take the potential infinite outside the pipe, but obviously by
itself that does not help much. You could assume infinite space
with a potential
if you then take the limit 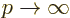 to get infinite potential
outside the pipe and zero inside. That gives the correct but trivial
result that all the energy is kinetic.)
to get infinite potential
outside the pipe and zero inside. That gives the correct but trivial
result that all the energy is kinetic.)
But the virial theorem does apply to any number of particles, not just
to one. Just sum over all the particles:
where i is the particle number.
For example, consider the hydrogen molecule, where there are four
particles, two protons and two electrons. Here
where 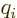 is
is 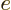 if particle
if particle  is a proton and
is a proton and 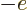 if it is an
electron. Like for the simple hydrogen atom,
if it is an
electron. Like for the simple hydrogen atom,
so the total expectation potential energy of the system is still twice
the total energy  and the total kinetic energy is still minus
and the total kinetic energy is still minus
 . And this continues to hold for much bigger systems of nuclei
and electrons, which is why it is of interest for computational
methods.
. And this continues to hold for much bigger systems of nuclei
and electrons, which is why it is of interest for computational
methods.
In some computations you might need to assume that the electrons are
in a state of definite energy, like in the ground state, but the
nuclei are not. In such computations the nuclei are at an assumed
position and you will only compute the state of the electrons. So the
summation in
now extends only over the electrons. But this summation does includes
potentials of the electrons due to the attraction by the nuclei, and
those terms are no longer equal to minus the corresponding potentials.
You may need to evaluate these terms explicitly. But that is not too
bad, as these potentials are now known functions of the individual
electron positions only. The difficult term, due to the
electron-electron interaction, is still given by minus the
corresponding potential.
Finally, you might wonder where the virial theorem comes from. Well,
one way to prove the virial theorem, as found in quantum textbooks and
on Wikipedia, is to work out the commutator in
using the formulae in chapter 4.5.4, to give
and then note that the left hand side above is zero for stationary
states, (in other words, for states with a precise total energy).
This follows the classical way of deriving the classical virial
theorem, but requires a messy purely mathematical derivation. The
theorem then pops up out of the complex mathematics without any
plausible physical reason why there would be such a theorem in the
first place.
The original derivation by Fock in 1930 is much more physically
appealing and more instructive. The idea is to slightly stretch the
given quantum system: replace every position coordinate coordinate
 by a slightly larger one
by a slightly larger one 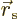

 . Here
. Here  is assumed to be a
vanishingly small number. We are interested in what the expectation
potential and kinetic energy are in this slightly stretched system.
is assumed to be a
vanishingly small number. We are interested in what the expectation
potential and kinetic energy are in this slightly stretched system.
First however, recall that the square magnitude of the wave function
gives the probability of that state, and that all probabilities must
integrate together to 1, certainty. Phrased differently, the
expectation value of one must be one; 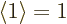 , what else? But
clearly, if you integrate the same square wave function magnitude
over a slightly larger domain, you will get a value slightly greater
than one. This problem is easily fixed, however, by multiplying the
wave function in the stretched system by a suitable constant slightly
less than one. Then
, what else? But
clearly, if you integrate the same square wave function magnitude
over a slightly larger domain, you will get a value slightly greater
than one. This problem is easily fixed, however, by multiplying the
wave function in the stretched system by a suitable constant slightly
less than one. Then  too. (The precise value of
the constant depends on the number of particles and is not important.)
too. (The precise value of
the constant depends on the number of particles and is not important.)
Next, the expectation kinetic energy consists of terms like
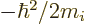 times
times 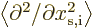 because of the form of the kinetic energy operator. Because of the
stretching of the coordinate in the bottom of the derivative, each of
these terms changes by a factor
because of the form of the kinetic energy operator. Because of the
stretching of the coordinate in the bottom of the derivative, each of
these terms changes by a factor  , so
, so
For the potential energy we can use a linear Taylor series to figure
out how it changes:
where in the right hand side  and its derivatives are
evaluated at
and its derivatives are
evaluated at 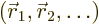 . From that
. From that
From the above expressions, it is seen that compared to the
unstretched system, in the stretched system the sum of expectation
kinetic and potential energies is different by an amount
But, as described in {A.7}, if you mess up an energy
wave function by an amount of order  , the expectation
energy should only be messed up by an amount proportional to
, the expectation
energy should only be messed up by an amount proportional to
 , not
, not  . (In brief, the amounts of the
other energy eigenfunctions found in the messed up wave function are
proportional to
. (In brief, the amounts of the
other energy eigenfunctions found in the messed up wave function are
proportional to  . However, the probabilities of their
energies are proportional to the squares of the amounts.) So the
factor between parentheses in the expression above must be zero, and
that is the virial theorem.
. However, the probabilities of their
energies are proportional to the squares of the amounts.) So the
factor between parentheses in the expression above must be zero, and
that is the virial theorem.
![]() .
.![]()
![]() .
.![]()
![]()
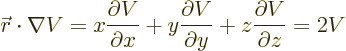
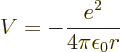
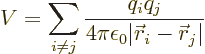
![]()
![]()
![]()
![]() .
.![]()
![]() ,
,![]()
![]()
![]()
![]() ,
,