| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
Subsections
A.6 Constant spherical potentials
This addendum describes the solutions of the Hamiltonian eigenvalue
problem in spherical coordinates if the potential is constant.
These solutions are important for many reasons. For example, you
might want to create a simplified model for the hydrogen atom that
way. To do so, you could, for example, assume that the potential
energy has a constant negative value up to say the Bohr radius and is
zero beyond it. That is not really a very good model for the hydrogen
atom. However, it works much better for nucleons in atomic nuclei,
chapter 14.12.
The solutions in this note are also important for describing
experiments in which particles are scattered from some target,
{A.30}. And more fundamentally, they give the energy
states of definite angular momentum for particles in empty space.
A.6.1 The eigenvalue problem
The Hamiltonian eigenvalue problem is
In this note it is assumed that the potential  is a constant in the
radial region of interest.
is a constant in the
radial region of interest.
To clean the problem up a bit, take the potential energy term to the
other side, and also the coefficient of the Laplacian. That produces
where
The constant  is what classical physics would take to be
the linear momentum of a particle with total energy
is what classical physics would take to be
the linear momentum of a particle with total energy  and potential
energy
and potential
energy  .
.
A.6.2 The eigenfunctions
Because the potential is spherically symmetric like for the hydrogen
atom, the eigenfunctions are of similar form:
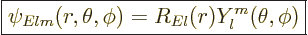 |
(A.17) |
Here the 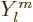 are again the spherical harmonics. These
eigenfunctions have definite square angular momentum
are again the spherical harmonics. These
eigenfunctions have definite square angular momentum  where
where  is an nonnegative integer. They also have definite angular
momentum in the chosen
is an nonnegative integer. They also have definite angular
momentum in the chosen  -direction equal to
-direction equal to 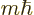 , where
, where
 is an integer that satisfies
is an integer that satisfies 

 .
.
The radial functions  in the eigenfunctions
in the eigenfunctions 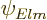 are
different from those of the hydrogen atom. Depending on whatever is
easiest in a given application, they can be written in two ways,
{D.16}.
are
different from those of the hydrogen atom. Depending on whatever is
easiest in a given application, they can be written in two ways,
{D.16}.
The first way is as
 |
(A.18) |
Here 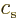 and
and 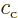 are arbitrary constants. The
functions
are arbitrary constants. The
functions 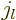 and
and 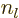 are called the “spherical Bessel functions” of the first and second kinds. The
are called the “spherical Bessel functions” of the first and second kinds. The
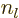 are also called the “Neumann functions” and might instead be indicated by
are also called the “Neumann functions” and might instead be indicated by 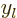 or
or
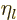 .
.
Expressions for these Bessel functions can be found in advanced
mathematical handbooks, [1]:
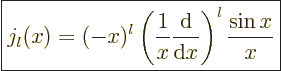 |
(A.19) |
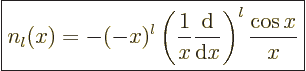 |
(A.20) |
The spherical Bessel functions are often convenient in a region of
constant potential that includes the origin, because the Bessel
functions of the first kind 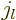 give the solutions that are finite
at the origin. (To see that, note that the Taylor series of
give the solutions that are finite
at the origin. (To see that, note that the Taylor series of  divided by
divided by  is a power series in
is a power series in 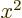 , and that
, and that 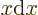

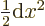 .) In particular for small
.) In particular for small  :
:
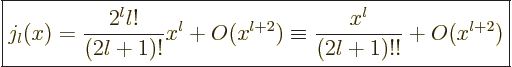 |
(A.21) |
Here !! is one of these unfortunate notations. The second ! means
that all even factors are dropped from the factorial.
The Bessel functions of the second kind are singular at the origin and
normally do not appear if the origin is part of the considered region.
Also, the spherical Bessel functions are real for real  .
However, in a region where the potential
.
However, in a region where the potential  is larger than the energy
is larger than the energy
 of the particles, the argument of the Bessel functions in
(A.18) will be imaginary.
of the particles, the argument of the Bessel functions in
(A.18) will be imaginary.
The other way to write the radial functions is as
where 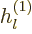 and
and  are called the “spherical Hankel functions.”
are called the “spherical Hankel functions.”
The spherical Hankel functions can again be found in advanced
mathematical handbooks, [1]:
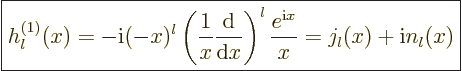 |
(A.22) |
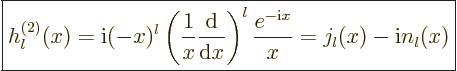 |
(A.23) |
The given expressions in terms of the spherical Bessel functions are
readily inverted to give the Bessel functions in terms of the Hankel
functions,
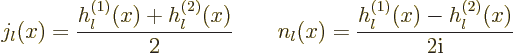 |
(A.24) |
For large  the spherical Hankel functions can be approximated as
the spherical Hankel functions can be approximated as
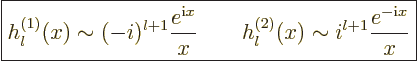 |
(A.25) |
This asymptotic behavior tends to make the Hankel functions more
convenient far from the origin. Exponentials are mathematically
simpler and more fundamental than the sines and cosines in the
asymptotic behavior of the Bessel functions.
A.6.3 About free space solutions
The most important case for which the energy eigenfunctions of the
previous subsection apply is for particles in empty space. They
describe energy states with definite square and  angular momentum.
However, sometimes particles in empty space are better described by
states of definite linear momentum. And in some cases, like in
scattering problems, you need both types of solution. Then you also
need to convert between them.
angular momentum.
However, sometimes particles in empty space are better described by
states of definite linear momentum. And in some cases, like in
scattering problems, you need both types of solution. Then you also
need to convert between them.
The energy states in empty space with definite square and  angular
momentum are
angular
momentum are
 |
(A.26) |
These states have square angular momentum  and angular
momentum in the chosen
and angular
momentum in the chosen  -direction
-direction  . They are
nonsingular at the origin.
. They are
nonsingular at the origin.
A state that has definite linear momentum  purely in
the
purely in
the  -direction has an energy eigenfunction
-direction has an energy eigenfunction
 |
(A.27) |
This eigenfunction is not normalized, and cannot be normalized.
However, neither can the eigenfunction 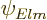 above be. It is
the curse of eigenfunctions in infinite empty space. An introduction
to the adjustments that must be made to deal with this is given in
chapter 7.9.
above be. It is
the curse of eigenfunctions in infinite empty space. An introduction
to the adjustments that must be made to deal with this is given in
chapter 7.9.
It is sometimes necessary to write a linear momentum eigenfunction of
the form (A.27) in terms of angular momentum ones of the
form (A.26). Rayleigh worked out the correct combination a
very long time ago, {D.16}:
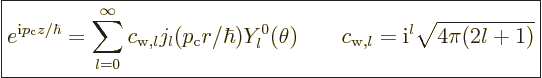 |
(A.28) |
Note that only eigenfunctions with 
 0 are needed.
0 are needed.
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]() .
.![]() :
:![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]() -
-