D.23 So­lu­tion of the hy­dro­gen mol­e­cule

To find the ap­prox­i­mate so­lu­tion for the hy­dro­gen mol­e­cule, the key is to be able to find the ex­pec­ta­tion en­ergy of the ap­prox­i­mate wave func­tions $a\psi_{\rm {l}}\psi_{\rm {r}}+b\psi_{\rm {r}}\psi_{\rm {l}}$.

First, for given $a$$\raisebox{.5pt}{$/$}$​$b$, the in­di­vid­ual val­ues of $a$ and $b$ can be com­puted from the nor­mal­iza­tion re­quire­ment

$$a^2+b^2 + 2ab \langle \psi_{\rm {l}} \vert \psi_{\rm {r}} \rangle^2 = 1$$ (D.11)

where the value of the over­lap in­te­gral $\langle\psi_{\rm {l}}\vert\psi_{\rm {r}}\rangle$ was given in de­riva­tion {D.21}.

The in­ner prod­uct

$$\langle a\psi_{\rm {l}}\psi_{\rm {r}}+b\psi_{\rm {r}}\psi_{... ...{\rm {l}}\psi_{\rm {r}}+b\psi_{\rm {r}}\psi_{\rm {l}}\rangle_6$$

is a six-di­men­sion­al in­te­gral, but when mul­ti­plied out, a lot of it can be fac­tored into prod­ucts of three-di­men­sion­al in­te­grals whose val­ues were given in de­riva­tion {D.21}. Clean­ing up the in­ner prod­uct, and us­ing the nor­mal­iza­tion con­di­tion, you can get:

$$\left\langle{E}\right\rangle = 2 E_1 - {\displaystyle\frac{... ...ab\langle\psi_{\rm {l}}\vert\psi_{\rm {r}}\rangle^2 A_2\Biggr]$$

us­ing the ab­bre­vi­a­tions

$$A_1 = 2\langle\psi_{\rm {l}}\vert r_{\rm {r}}^{-1}\psi_{\rm... ...{\rm {r}}\vert r_{12}^{-1}\psi_{\rm {l}}\psi_{\rm {r}}\rangle$$

$$A_2 = {\displaystyle\frac{2\langle\psi_{\rm {l}}\vert r_{... ...{\rm {r}}\vert r_{12}^{-1}\psi_{\rm {l}}\psi_{\rm {r}}\rangle$$

Val­ues for sev­eral of the in­ner prod­ucts in these ex­pres­sions are given in de­riva­tion {D.21}. Un­for­tu­nately, these in­volv­ing the dis­tance $r_{12}$ $\vphantom0\raisebox{1.5pt}{$=$}$ $\vert{\skew0\vec r}_1-{\skew0\vec r}_2\vert$ be­tween the elec­trons can­not be done an­a­lyt­i­cally. And one of the two can­not even be re­duced to a three-di­men­sion­al in­te­gral, and needs to be done in six di­men­sions. (It can be re­duced to five di­men­sions, but that in­tro­duces a nasty sin­gu­lar­ity and stick­ing to six di­men­sions seems a bet­ter idea.) So, it gets re­ally elab­o­rate, be­cause you have to en­sure nu­mer­i­cal ac­cu­racy for sin­gu­lar, high-di­men­sion­al in­te­grals. Still, it can be done with some per­se­ver­ance.

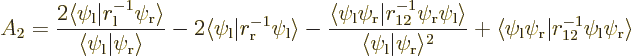
In any case, the ba­sic idea is still to print out ex­pec­ta­tion en­er­gies, easy to ob­tain or not, and to ex­am­ine the print-out to see at what val­ues of $a$$\raisebox{.5pt}{$/$}$​$b$ and $d$ the en­ergy is min­i­mal. That will be the ground state.

The re­sults are listed in the main text, but here are some more data that may be of in­ter­est. At the 1.62 $a_0$ nu­clear spac­ing of the ground state, the an­ti­sym­met­ric state $a$$\raisebox{.5pt}{$/$}$​$b$ $\vphantom0\raisebox{1.5pt}{$=$}$ $\vphantom{0}\raisebox{1.5pt}{$-$}$1 has a pos­i­tive en­ergy of 7 eV above sep­a­rate atoms and is there­fore un­sta­ble.

The nu­cleus to elec­tron at­trac­tion en­er­gies are 82 eV for the sym­met­ric state, and 83.2 eV for the an­ti­sym­met­ric state, so the an­ti­sym­met­ric state has the lower po­ten­tial en­ergy, like in the hy­dro­gen mol­e­c­u­lar ion case, and un­like what you read in some books. The sym­met­ric state has the lower en­ergy be­cause of lower ki­netic en­ergy, not po­ten­tial en­ergy.

Due to elec­tron cloud merg­ing, for the sym­met­ric state the elec­tron to elec­tron re­pul­sion en­ergy is 3 eV lower than you would get if the elec­trons were point charges lo­cated at the nu­clei. For the an­ti­sym­met­ric state, it is 5.8 eV lower.

As a con­se­quence, the an­ti­sym­met­ric state also has less po­ten­tial en­ergy with re­spect to these re­pul­sions. Adding it all to­gether, the sym­met­ric state has quite a lot less ki­netic en­ergy than the an­ti­sym­met­ric one.