| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
D.24 Hydrogen molecule ground state and spin
The purpose of this note is to verify that the inclusion of spin does
not change the spatial form of the ground state of the hydrogen
molecule. The lowest expectation energy 

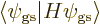 , characterizing
the correct ground state, only occurs if all spatial components
, characterizing
the correct ground state, only occurs if all spatial components
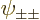 of the ground state with spin,
of the ground state with spin,
are proportional to the no-spin spatial ground state
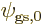 .
.
The reason is that the assumed Hamiltonian (5.3) does not
involve spin at all, only spatial coordinates, so, for example,
and the same for the other three terms in 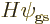 . So
the expectation value of energy becomes
. So
the expectation value of energy becomes
Because of the orthonormality of the spin states, this multiplies
out into inner products of matching spin states as
In addition, the wave function must be normalized,
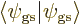
 1, or
1, or
Now when 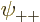 ,
, 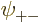 ,
, 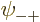 , and
, and
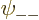 are each proportional to the no-spin spatial ground state
are each proportional to the no-spin spatial ground state
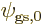 with the lowest energy
with the lowest energy 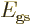 , their
individual contributions to the energy will be given by
, their
individual contributions to the energy will be given by
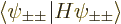

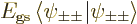 , the lowest
possible. Then the total energy
, the lowest
possible. Then the total energy  will be
will be 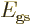 .
Anything else will have more energy and can therefore not be the
ground state.
.
Anything else will have more energy and can therefore not be the
ground state.
It should be pointed out that to a more accurate approximation, spin
causes the electrons to be somewhat magnetic, and that produces a
slight dependence of the energy on spin; compare addendum
{A.39}. This note ignored that, as do most other
derivations in this book.
![]()
![]()
![]() ,
,![]()

![]()
![]()