| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
A.34 Explanation of Hund’s first rule
Hund’s first rule of spin-alignment applies because electrons in
atoms prefer to go into spatial states that are antisymmetric with
respect to electron exchange. Spin alignment is then an unavoidable
consequence of the weird antisymmetrization requirement.
To understand why electrons want to go into antisymmetric spatial
states, the interactions between the electrons need to be
considered. Sweeping them below the carpet as the discussion of atoms
in chapter 5.9 did is not going to cut it.
To keep it as simple as possible, the case of the carbon atom will be
considered. As the crude model of chapter 5.9 did
correctly deduce, the carbon atom has two 1s electrons locked into a
zero-spin singlet state, and similarly two 2s electrons also in a
singlet state. Hund’s rule is about the final two electrons that
are in 2p states. As far as the simple model of chapter
5.9 was concerned, these electrons can do whatever they
want within the 2p subshell.
To go one better than that, the correct interactions between the two
2p electrons will need to be considered. To keep the arguments
manageable, it will still be assumed that the effects of the 1s and 2s
electrons are independent of where the 2p electrons are.
Call the 2p electrons  and
and 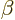 . Under the stated
conditions, their Hamiltonian takes the form
. Under the stated
conditions, their Hamiltonian takes the form
where 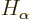 and
and 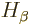 are the single-electron Hamiltonians
for the electrons
are the single-electron Hamiltonians
for the electrons  and
and 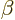 , consisting of their
kinetic energy, their attraction to the nucleus, and the repulsion by
the 1s and 2s electrons. Note that in the current analysis, it is not
required that the 1s and 2s electrons are treated as located in the
nucleus. Lack of shielding can be allowed now, but it must still be
assumed that the 1s and 2s electrons are unaffected by where the 2p
electrons are. In particular,
, consisting of their
kinetic energy, their attraction to the nucleus, and the repulsion by
the 1s and 2s electrons. Note that in the current analysis, it is not
required that the 1s and 2s electrons are treated as located in the
nucleus. Lack of shielding can be allowed now, but it must still be
assumed that the 1s and 2s electrons are unaffected by where the 2p
electrons are. In particular, 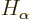 is assumed to be be
independent of the position of electron
is assumed to be be
independent of the position of electron 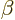 , and
, and 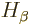 independent of the position of electron
independent of the position of electron  . The mutual
repulsion of the two 2p electrons is given by
. The mutual
repulsion of the two 2p electrons is given by 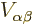

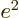

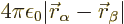 .
.
Now assume that electrons  and
and 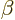 appropriate two
single-electron spatial 2p states for themselves, call them
appropriate two
single-electron spatial 2p states for themselves, call them  and
and  . For carbon,
. For carbon,  can be thought of as the
2p
can be thought of as the
2p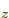 state and
state and  as the 2p
as the 2p state, The
general spatial wave function describing the two electrons takes the
generic form
state, The
general spatial wave function describing the two electrons takes the
generic form
The two states  and
and  will be taken to be orthonormal,
like p
will be taken to be orthonormal,
like p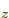 and p
and p are, and then the normalization
requirement is that
are, and then the normalization
requirement is that 
 1.
1.
The expectation value of energy is
That can be multiplied out and then simplified by noting that in the
various inner product integrals involving the single-electron
Hamiltonians, the integral over the coordinate unaffected by the
Hamiltonian is either zero or one because of orthonormality. Also,
the inner product integrals involving 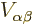 are pairwise
the same, the difference being just a change of names of integration
variables.
are pairwise
the same, the difference being just a change of names of integration
variables.
The simplified expectation energy is then:
The first two terms are the single-electron energies of states
 and
and  . The third term is the classical
repulsion between between two electron charge distributions of
strengths
. The third term is the classical
repulsion between between two electron charge distributions of
strengths  and
and 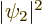 . The electrons minimize
this third term by going into spatially separated states like the
2p
. The electrons minimize
this third term by going into spatially separated states like the
2p and 2p
and 2p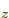 ones, rather than into the same
spatial state or into greatly overlapping ones.
ones, rather than into the same
spatial state or into greatly overlapping ones.
The final one of the four terms is the interesting one for
Hund’s rule; it determines how the two electrons occupy the
two states  and
and  , symmetrically or
antisymmetrically. Consider the detailed expression for the inner
product integral appearing in the term:
, symmetrically or
antisymmetrically. Consider the detailed expression for the inner
product integral appearing in the term:
where 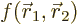

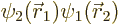 .
.
The sign of this inner product can be guesstimated. If
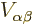 would be the same for all electron separation
distances, the integral would be zero because of orthonormality of
would be the same for all electron separation
distances, the integral would be zero because of orthonormality of
 and
and  . However,
. However, 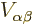 favors
positions where
favors
positions where 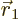 and
and 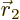 are close to each other; in fact
are close to each other; in fact
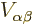 is infinitely large if
is infinitely large if 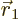

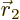 .
At such a location
.
At such a location 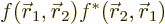 is a positive real
number, so it tends to have a positive real part in regions it really
counts. That means the inner product integral should have the same
sign as
is a positive real
number, so it tends to have a positive real part in regions it really
counts. That means the inner product integral should have the same
sign as 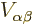 ; it should be repulsive.
; it should be repulsive.
And since this integral is multiplied by  , the energy
is smallest when that is most negative, which is for the antisymmetric
spatial state
, the energy
is smallest when that is most negative, which is for the antisymmetric
spatial state 


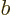 . Since this state takes care of
the sign change in the antisymmetrization requirement, the spin state
must be unchanged under particle exchange; the spins must be aligned.
More precisely, the spin state must be some linear combination of the
three triplet states with net spin one. There you have Hund’s
rule, as an accidental byproduct of the Coulomb repulsion.
. Since this state takes care of
the sign change in the antisymmetrization requirement, the spin state
must be unchanged under particle exchange; the spins must be aligned.
More precisely, the spin state must be some linear combination of the
three triplet states with net spin one. There you have Hund’s
rule, as an accidental byproduct of the Coulomb repulsion.
This leaves the philosophical question why for the two electrons of
the hydrogen molecule in chapter 5.2 the symmetric state is
energetically most favorable, while the antisymmetric state is the one
for the 2p electrons. The real difference is in the kinetic energy.
In both cases, the antisymmetric combination reduces the Coulomb
repulsion energy between the electrons, and in the hydrogen molecule
model, it also increases the nuclear attraction energy. But in the
hydrogen molecule model, the symmetric state achieves a reduction in
kinetic energy that is more than enough to make up for it all. For the
2p electrons, the reduction in kinetic energy is nil. When the
positive component wave functions of the hydrogen molecule model are
combined into the symmetric state, they allow greater access to fringe
areas farther away from the nuclei. Because of the uncertainty
principle, less confined electrons tend to have less indeterminacy in
momentum, hence less kinetic energy. On the other hand, the 2p states
are half positive and half negative, and even their symmetric
combination reduces spatial access for the electrons in half the
locations.
![]()
![]() .
.![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]() ,
,
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]() ;
;![]() ,
,![]()
![]()
![]()
![]() .
.