|
|
|
|
|
Next: A.36 Alternate Dirac equations |
|
In the simplest formulation, the third law of thermodynamics says that the entropy at absolute zero temperature is zero.
The original theorem is due to Nernst. A more recent formulation is
“The contribution to the entropy of a system due to each component that is in internal equilibrium disappears at absolute zero.” [D. Ter Haar (1966) Elements of Thermostatistics. Holt, Rinehart & Winston.]A more readable version is
“The entropy of every chemically simple, perfectly crystalline, body equals zero at the absolute zero of temperature.” [G.H. Wannier (1966) Statistical Physics. Wiley.]These formulations allow for the existence of meta-stable equilibria. The third law in its simple form assumes that strictly speaking every ground state is reasonably unique and that the system is in true thermal equilibrium. Experimentally however, many substances do not appear to approach zero entropy. Random mixtures as well as ice are examples. They may not be in true equilibrium, but if true equilibrium is not observed, it is academic.
The zero of entropy is important for mixtures, in which you need to
add the entropies of the components together correctly. It also has
implications for the behavior of various quantities at low
temperatures. For example, it implies that the specific heats become
zero at absolute zero. To see why, note that in a constant volume or
constant pressure process the entropy changes are given by
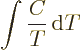
Another consequence of the third law is that it is not possible to bring a system to absolute zero temperature completely even in ideal processes. That seems pretty self-evident from a classical point of view, but it is not so obvious in quantum terms. The third law also implies that isothermal processes become isentropic when absolute zero temperature is approached.
It may seem that the third law is a direct consequence of the quantum
expression for the entropy,
Even if the ground state is not unique, often it does not make much of
a difference. For example, consider the case of a system of ![]()
![]()
![]()
![]() .
.![]()
![]()
![]() ,
,
On the other hand, if you ignore electromagnetic spin couplings of nuclei in a crystal, it becomes a different matter. Since the nuclear wave functions have no measurable overlap, to any conceivable accuracy the nuclei can assume independent spatial states. That gets rid of the (anti) symmetrization restrictions on their spin. And then the associated entropy can be nonzero. But of course, if the nuclear spin does not interact with anything, you may be able to ignore its existence altogether.
Even if a system has a unique ground state, the third law is not as
trivial as it may seem. Thermodynamics deals not with finite systems
but with idealized systems of infinite size. A very simple example
illustrates why it makes a difference. Consider the possibility of a
hypothetical system whose specific entropy depends on the number of
particles ![]() ,
,![]() ,
,![]()
If infinite systems seem unphysical, translate it into real-life
terms. Suppose your test tube has say ![]()
![]()
![]()
![]()