| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
D.31 Integral Schrödinger equation
In this note, the integral Schrödinger equation is derived from the
partial differential equation version.
First the time-independent Schrödinger equation is rewritten
in the form
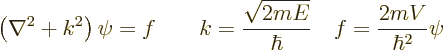 |
(D.16) |
The left equation is known as the “Helmholtz equation.”
The Helmholtz equation is not at all specific to quantum mechanics.
In general it describes basic wave propagation at a frequency related
to the value of the constant  . The right hand side
. The right hand side  describes the amount of wave motion that is created at a given
location. Quantum mechanics is somewhat weird in that
describes the amount of wave motion that is created at a given
location. Quantum mechanics is somewhat weird in that  involves
the unknown wave function
involves
the unknown wave function  that you want to find. In simpler
applications,
that you want to find. In simpler
applications,  is a given function.
is a given function.
The general solution to the Helmholtz equation can be written as
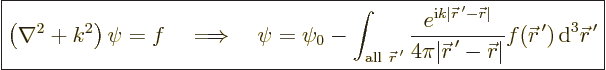 |
(D.17) |
Here 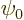 is any solution of the homogeneous Helmholtz
equation, the equation without
is any solution of the homogeneous Helmholtz
equation, the equation without  .
.
To see why this is the solution of the Helmholtz equation requires a
bit of work. First consider the solution of the Helmholtz equation
for the special case that  is a delta function at the origin:
is a delta function at the origin:
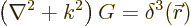
The solution  to this problem is called the “Green’s
function of the Helmholtz equation.
to this problem is called the “Green’s
function of the Helmholtz equation.
The Green’s function can be found relatively easily. Away from
the origin  is a solution of the homogeneous Helmholtz equation,
because the delta function is everywhere zero except at the origin.
In terms of quantum mechanics, the homogeneous Helmholtz equation
means a particle in free space,
is a solution of the homogeneous Helmholtz equation,
because the delta function is everywhere zero except at the origin.
In terms of quantum mechanics, the homogeneous Helmholtz equation
means a particle in free space, 
 0. Possible solutions for
0. Possible solutions for
 are then spherical harmonics times spherical Hankel functions of
the first and second kinds, {A.6}. However, Hankel
functions of the first kind are preferred for physical reasons; they
describe waves that propagate away from the region of wave generation
to infinity. Hankel functions of the second kind describe waves that
come in from infinity. Incoming waves, if any, are usually much more
conveniently described using the homogeneous solution
are then spherical harmonics times spherical Hankel functions of
the first and second kinds, {A.6}. However, Hankel
functions of the first kind are preferred for physical reasons; they
describe waves that propagate away from the region of wave generation
to infinity. Hankel functions of the second kind describe waves that
come in from infinity. Incoming waves, if any, are usually much more
conveniently described using the homogeneous solution 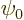 .
.
Further, since the problem for  is spherically symmetric, the
solution should not depend on the angular location. The spherical
harmonic must be the constant
is spherically symmetric, the
solution should not depend on the angular location. The spherical
harmonic must be the constant  . That makes the correct
solution a multiple of the spherical Hankel function
. That makes the correct
solution a multiple of the spherical Hankel function
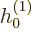 , which means proportional to
, which means proportional to
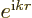

 . You can easily check by direct substitution
that this does indeed satisfy the homogeneous Helmholtz equation away
from the origin in spherical coordinates.
. You can easily check by direct substitution
that this does indeed satisfy the homogeneous Helmholtz equation away
from the origin in spherical coordinates.
To get the correct constant of proportionality, integrate the
Helmholtz equation for  above over a small sphere around the
origin. In the right hand side use the fact that the integral of a
delta function is by definition equal to 1. In the left hand side,
use the divergence theorem to avoid having to try to integrate the
singular second order derivatives of
above over a small sphere around the
origin. In the right hand side use the fact that the integral of a
delta function is by definition equal to 1. In the left hand side,
use the divergence theorem to avoid having to try to integrate the
singular second order derivatives of  at the origin. That shows
that the complete Green’s function is
at the origin. That shows
that the complete Green’s function is
(You might worry about the mathematical justification for these
manipulations. Singular functions like  are not proper solutions
of partial differential equations. However, the real objective is to
find the limiting solution
are not proper solutions
of partial differential equations. However, the real objective is to
find the limiting solution  when a slightly smoothed delta function
becomes truly singular. The described manipulations are justified in
this limiting process.)
when a slightly smoothed delta function
becomes truly singular. The described manipulations are justified in
this limiting process.)
The next step is to solve the Helmholtz equation for an arbitrary
right hand side  , rather than a delta function. To do so,
imagine the region subdivided into infinitely many infinitesimal
volume elements
, rather than a delta function. To do so,
imagine the region subdivided into infinitely many infinitesimal
volume elements 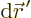 . In each volume element,
approximate the function
. In each volume element,
approximate the function  by a delta function spike
by a delta function spike
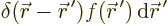 . Such a spike integrates
to the same value as
. Such a spike integrates
to the same value as  does over the volume element. Each spike
produces a solution given by
does over the volume element. Each spike
produces a solution given by
Integrate over all volume elements to get the solution of the
Helmholtz equation (D.17). Substitute in what  is for
the Schrödinger equation to get the integral Schrödinger equation.
is for
the Schrödinger equation to get the integral Schrödinger equation.
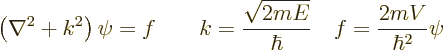
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]() .
.![]() ,
,![]()
![]()
![]() .
.![]()
![]()
![]() ,
,![]() .
.![]()
![]() .
.![]()