| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
D.30 Number of conduction band electrons
This note finds the number of electrons in the conduction band of a
semiconductor, and the number of holes in the valence band.
By definition, the density of states 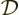 is the number of
single-particle states per unit energy range and unit volume. The
fraction of electrons in those states is given by
is the number of
single-particle states per unit energy range and unit volume. The
fraction of electrons in those states is given by
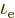 . Therefore the number of electrons in the
conduction band per unit volume is given by
. Therefore the number of electrons in the
conduction band per unit volume is given by
where 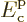 is the energy at the bottom of the conduction
band and
is the energy at the bottom of the conduction
band and 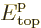 that at the top of the band.
that at the top of the band.
To compute this integral, for 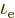 the Maxwell-Boltzmann
expression (6.33) can be used, since the number of electrons
per state is invariably small. And for the density of states the
expression (6.6) for the free-electron gas can be used if
you substitute in a suitable effective mass of the electrons and
replace
the Maxwell-Boltzmann
expression (6.33) can be used, since the number of electrons
per state is invariably small. And for the density of states the
expression (6.6) for the free-electron gas can be used if
you substitute in a suitable effective mass of the electrons and
replace  by
by  .
.
Also, because 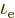 decreases extremely rapidly with
energy, only a very thin layer at the bottom of the conduction band
makes a contribution to the number of electrons. The integrand of the
integral for
decreases extremely rapidly with
energy, only a very thin layer at the bottom of the conduction band
makes a contribution to the number of electrons. The integrand of the
integral for 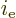 is essentially zero above this layer.
Therefore you can replace the upper limit of integration with infinity
without changing the value of
is essentially zero above this layer.
Therefore you can replace the upper limit of integration with infinity
without changing the value of 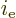 . Now use a change of
integration variable to
. Now use a change of
integration variable to 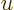

 and an integration by parts to reduce the integral to the one found
under
and an integration by parts to reduce the integral to the one found
under !
in the notations section. The result is as
stated in the text.
For holes, the derivation goes the same way if you use 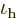 from (6.34) and integrate over the valence band energies.
from (6.34) and integrate over the valence band energies.
![]()
![]() .
.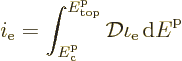
![]()
![]()
![]() .
.![]()
![]()
![]() .
.![]()
![]()
![]()
![]()