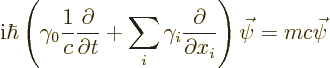| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
A.36 Alternate Dirac equations
If you look in advanced books on quantum mechanics, you will likely
find the Dirac equation written in a different form than given in
chapter 12.12.
The Hamiltonian eigenvalue problem as given in that section was
where 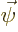 was a vector with four components.
was a vector with four components.
Now assume for a moment that  is a state of definite momentum.
Then the above equation can be rewritten in the form
is a state of definite momentum.
Then the above equation can be rewritten in the form
The motivation for doing so is that the coefficients of the  matrices are the components of the relativistic momentum four-vector,
chapter 1.3.1.
matrices are the components of the relativistic momentum four-vector,
chapter 1.3.1.
It is easy to check that the only difference between the  and
and
 matrices is that
matrices is that 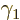 through
through 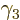 get a minus
sign in front of their bottom element. (Just multiply the original
equation by
get a minus
sign in front of their bottom element. (Just multiply the original
equation by 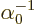

 and rearrange.)
and rearrange.)
The parenthetical expression above is essentially a four-vector dot
product between the gamma matrices and the momentum four-vector.
Especially if you give the dot product the wrong sign, as many
physicists do. In particular, in the index notation of chapter
1.2.5, the parenthetical expression is then
 . Feynman hit upon the bright idea to
indicate dot products with
. Feynman hit upon the bright idea to
indicate dot products with  matrices by a slash through the
name. So you are likely to find the above equation as
matrices by a slash through the
name. So you are likely to find the above equation as
Isn’t it beautifully concise? Isn’t it completely
incomprehensible?
Also consider the case that 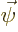 is not an energy and momentum
eigenfunction. In that case, the equation of interest is found from
the usual quantum substitutions that
is not an energy and momentum
eigenfunction. In that case, the equation of interest is found from
the usual quantum substitutions that  becomes
becomes
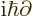

 and
and 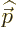 becomes
becomes


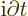 . So the rewritten Dirac
equation is then:
. So the rewritten Dirac
equation is then:
In index notation, the parenthetical expression reads
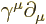 . So following Feynman
. So following Feynman
Now all that the typical physics book wants to add to that is a
suitable non-SI system of units. If you use the electron mass  as
your unit of mass instead of the kg,
as
your unit of mass instead of the kg,  as unit of velocity instead
of m/s, and
as unit of velocity instead
of m/s, and  as your unit of angular momentum
instead of kg m
as your unit of angular momentum
instead of kg m /s, you get
/s, you get
No outsider will ever guess what that stands for!
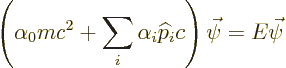
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.