| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
Subsections
A.39 The relativistic hydrogen atom
The description of the hydrogen atom given earlier in chapter
4.3 is very accurate by engineering standards. However, it
is not exact. This addendum examines various relativistic effects
that were ignored in the analysis.
The approach will be to take the results of chapter 4.3 as
the starting point. Then corrections are applied to them using
perturbation theory as described in addendum {A.38}.
A.39.1 Introduction
According to the description of the hydrogen atom given in chapter
4.3, all energy eigenfunctions 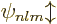 with the
same value of
with the
same value of  have the same energy
have the same energy 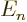 . Therefore they
should show up as a single line in an experimental line spectrum. But
actually, when these spectra are examined very precisely, the
. Therefore they
should show up as a single line in an experimental line spectrum. But
actually, when these spectra are examined very precisely, the 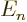 energy levels for a given value of
energy levels for a given value of  are found to consist of several
closely spaced lines, rather than a single one. That is called the
are found to consist of several
closely spaced lines, rather than a single one. That is called the
hydrogen atom fine structure.
It means that
eigenfunctions that all should have exactly the same energy,
don’t.
To explain why, the solution of chapter 4.3 must be
corrected for a variety of relativistic effects. Before doing so, it
is helpful to express the nonrelativistic energy levels of that
chapter in terms of the rest mass energy
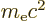 of
the electron, as follows:
of
the electron, as follows:
 |
(A.247) |
The constant  is called the “fine structure constant.” It combines the constants
is called the “fine structure constant.” It combines the constants
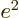

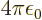 from electromagnetism,
from electromagnetism,  from quantum
mechanics, and the speed of light
from quantum
mechanics, and the speed of light  from relativity into one
nondimensional number. It is without doubt the single most important
number in all of physics, [19].
from relativity into one
nondimensional number. It is without doubt the single most important
number in all of physics, [19].
Nobody knows why it has the value that it has. Still, obviously it is
a measurable value, so, following the stated ideas of quantum
mechanics, maybe the universe measured
this value
during its early formation by a process that we may never understand,
(since we do not have other measured values for  to deduce any
properties of that process from.) If you have a demonstrably better
explanation, Sweden awaits you.
to deduce any
properties of that process from.) If you have a demonstrably better
explanation, Sweden awaits you.
In any case, for engineering purposes it is a small number, less than
1%. That makes the hydrogen energy levels really small compared to
the rest mass energy of the electron, because they are proportional to
the square of  , which is as small as 0.005%. In simple
terms, the electron in hydrogen stays well clear of the speed of
light.
, which is as small as 0.005%. In simple
terms, the electron in hydrogen stays well clear of the speed of
light.
And that in turn means that the relativistic errors in the hydrogen
energy levels are small. Still, even small errors can sometimes be
very important. The required corrections are listed below in order of
decreasing magnitude.
- Fine structure.
The electron should really be described relativistically using the
Dirac equation instead of classically. In classical terms, that
will introduce three corrections to the energy levels:
- Einstein’s relativistic correction of the classical
kinetic energy
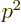

 of the electron.
of the electron.
Spin-orbit interaction
, due to the fact that
the spin of the moving electron changes the energy levels. The
spin of the electron makes it act like a little electromagnet. It
can be seen from classical electrodynamics that a moving magnet
will interact with the electric field of the nucleus, and that
changes the energy levels. Note that the name spin-orbit interaction
is a well chosen one, a rarity in physics.
- There is a third correction for states of zero angular
momentum, the Darwin term. It is a crude fix for the fundamental
problem that the relativistic wave function is not just a modified
classical one, but also involves interaction with the
anti-particle of the electron, the positron.
Fortunately, all three of these effects are very small; they are
smaller than the uncorrected energy levels by a factor of order
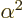 , and the error they introduce is on the order of
0.001%. So the
, and the error they introduce is on the order of
0.001%. So the exact
solution of chapter
4.3 is, by engineering standards, pretty exact after all.
- Lamb shift. Relativistically, the electron is affected by
virtual photons and virtual electron-positron pairs. It adds a
correction of relative magnitude
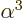 to the energy levels,
one or two orders of magnitude smaller still than the fine structure
corrections. To understand the correction properly requires quantum
electrodynamics.
to the energy levels,
one or two orders of magnitude smaller still than the fine structure
corrections. To understand the correction properly requires quantum
electrodynamics.
- Hyperfine splitting. Like the electron, the proton acts
as a little electromagnet too. Therefore the energy depends on how
it aligns with the magnetic field generated by the electron. This
effect is a factor
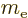

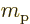 smaller still than the fine structure
corrections, making the associated energy changes about two orders
of magnitude smaller.
smaller still than the fine structure
corrections, making the associated energy changes about two orders
of magnitude smaller.
Hyperfine splitting couples the spins of proton and electron, and in
the ground state, they combine in the singlet state. A slightly
higher energy level occurs when they are in a spin-one triplet
state; transitions between these states radiate very low energy
photons with a wave length of 21 cm. This is the source of the
21 centimeter line” or “hydrogen line
radiation that is of great importance in cosmology. For example, it
has been used to analyze the spiral arms of the galaxy, and the hope
at the time of this writing is that it can shed light on the so
called dark ages
that the universe went through.
Since so little energy is released, the transition is very slow,
chapter 7.6.1. It takes on the order of 10 million
years, but that is a small time on the scale of the universe.
The message to take away from that is that even errors in the ground
state energy of hydrogen that are two million times smaller than the
energy itself can be of critical importance under the right
conditions.
The following subsections discuss each correction in more detail.
A.39.2 Fine structure
From the Dirac equation, it can be seen that three terms need to be
added to the nonrelativistic Hamiltonian of chapter 4.3 to
correct the energy levels for relativistic effects. The three terms
are worked out in derivation {D.81}. But that
mathematics really provides very little insight. It is much more
instructive to try to understand the corrections from a more physical
point of view.
The first term is relatively easy to understand. Consider
Einstein’s famous relation 

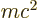 , where
, where  is
energy,
is
energy,  mass, and
mass, and  the speed of light. According to this
relation, the kinetic energy of the electron is not
the speed of light. According to this
relation, the kinetic energy of the electron is not
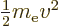 , with
, with 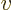 the velocity, as Newtonian physics
says. Instead it is the difference between the energy
the velocity, as Newtonian physics
says. Instead it is the difference between the energy
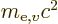 based on the mass
based on the mass 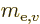 of the electron
in motion and the energy
of the electron
in motion and the energy 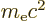 based on the mass
based on the mass 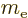 of the
electron at rest. In terms of momentum
of the
electron at rest. In terms of momentum 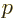

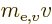 , chapter 1.1.2,
, chapter 1.1.2,
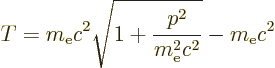 |
(A.248) |
Since the speed of light is large compared to the typical speed of the
electron, the square root can be expanded in a Taylor series,
[41, 22.12], to give:
The first term corresponds to the kinetic energy operator used in the
nonrelativistic quantum solution of chapter 4.3. (It may be
noted that the relativistic momentum 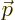 is based on the moving mass
of the electron, not its rest mass. It is this relativistic momentum
that corresponds to the operator
is based on the moving mass
of the electron, not its rest mass. It is this relativistic momentum
that corresponds to the operator 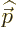

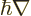

 . So the Hamiltonian used in chapter
4.3 was a bit relativistic already, because in replacing
. So the Hamiltonian used in chapter
4.3 was a bit relativistic already, because in replacing
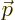 by
by 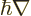

 , it used the relativistic
expression.) The second term in the Taylor series expansion above is
the first of the corrections needed to fix up the hydrogen energy
levels for relativity. Rewritten in terms of the square of the
classical kinetic energy operator, the Bohr ground state energy
, it used the relativistic
expression.) The second term in the Taylor series expansion above is
the first of the corrections needed to fix up the hydrogen energy
levels for relativity. Rewritten in terms of the square of the
classical kinetic energy operator, the Bohr ground state energy 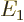 and the fine structure constant
and the fine structure constant  , it is
, it is
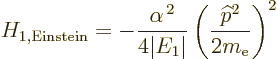 |
(A.249) |
The second correction that must be added to the nonrelativistic
Hamiltonian is the so-called spin-orbit interaction.
In classical terms, it is due to the spin of the electron, which makes
it into a magnetic dipole.
Think of it as a magnet of
infinitesimally small size, but with infinitely strong north and
south poles to make up for it. The product of the infinitesimal
vector from south to north pole times the infinite strength of the
poles is finite, and defines the magnetic dipole moment
 . By itself, it is quite inconsequential since the
magnetic dipole does not interact directly with the electric field of
the nucleus. However, moving magnetic poles create an electric
field just like the moving electric charges in an electromagnet
create a magnetic field. The electric fields generated by the moving
magnetic poles of the electron are opposite in strength, but not quite
centered at the same position. Therefore they correspond to a
motion-induced electric dipole. And an electric dipole does
interact with the electric field of the nucleus; it wants to align
itself with it. That is just like the magnetic dipole wanted to align
itself with the external magnetic field in the Zeeman effect.
. By itself, it is quite inconsequential since the
magnetic dipole does not interact directly with the electric field of
the nucleus. However, moving magnetic poles create an electric
field just like the moving electric charges in an electromagnet
create a magnetic field. The electric fields generated by the moving
magnetic poles of the electron are opposite in strength, but not quite
centered at the same position. Therefore they correspond to a
motion-induced electric dipole. And an electric dipole does
interact with the electric field of the nucleus; it wants to align
itself with it. That is just like the magnetic dipole wanted to align
itself with the external magnetic field in the Zeeman effect.
So how big is this effect? Well, the energy of an electric dipole
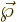 in an electric field
in an electric field  is
is
As you might guess, the electric dipole generated by the magnetic
poles of the moving electron is proportional to the speed of the
electron  and its magnetic dipole moment
and its magnetic dipole moment  .
More precisely, the electric dipole moment
.
More precisely, the electric dipole moment 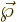 will be
proportional to
will be
proportional to 

 because if the vector
connecting the south and north poles is parallel to the motion, you do
not have two neighboring currents of magnetic poles, but a single
current of both negative and positive poles that completely cancel
each other out. Also, the electric field
because if the vector
connecting the south and north poles is parallel to the motion, you do
not have two neighboring currents of magnetic poles, but a single
current of both negative and positive poles that completely cancel
each other out. Also, the electric field  of the nucleus is
minus the gradient of its potential
of the nucleus is
minus the gradient of its potential 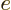

 , so
, so
Now the order of the vectors in this triple product can be changed,
and the dipole strength  of the electron equals its spin
of the electron equals its spin
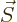 times the charge per unit mass
times the charge per unit mass 
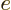

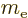 , so
, so
The expression between the parentheses is the angular momentum
 save for the electron mass. The constant of proportionality
is worked out in derivation {D.82}, giving the spin-orbit
Hamiltonian as
save for the electron mass. The constant of proportionality
is worked out in derivation {D.82}, giving the spin-orbit
Hamiltonian as
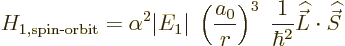 |
(A.250) |
The final correction that must be added to the nonrelativistic
Hamiltonian is the so-called “Darwin term:”
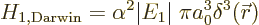 |
(A.251) |
According to its derivation in {D.81}, it is a crude
fix-up for an interaction with a virtual positron that simply cannot
be included correctly in a nonrelativistic analysis.
If that is not very satisfactory, the following much more detailed
derivation can be found on the web. It does succeed in
explaining the Darwin term fully within the nonrelativistic picture
alone. First assume that the electric potential of the nucleus does
not really become infinite as 1
 at
at 
 0, but is smoothed
out over some finite nuclear size. Also assume that the electron does
not
0, but is smoothed
out over some finite nuclear size. Also assume that the electron does
not see
this potential sharply, but perceives of its
features a bit vaguely, as diffused out symmetrically over a typical
distance equal to the so-called Compton wave length


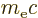 . There are several plausible reasons why it
might: (1) the electron has illegally picked up a chunk of a negative
rest mass state, and it is trembling with fear that the uncertainty in
energy will be noted, moving rapidly back and forwards over a Compton
wave length in a so-called
. There are several plausible reasons why it
might: (1) the electron has illegally picked up a chunk of a negative
rest mass state, and it is trembling with fear that the uncertainty in
energy will be noted, moving rapidly back and forwards over a Compton
wave length in a so-called Zitterbewegung
; (2) the
electron has decided to move at the speed of light, which is quite
possible nonrelativistically, so its uncertainty in position is of
the order of the Compton wave length, and it just cannot figure out
where the right potential is with all that uncertainty in position and
light that fails to reach it; (3) the electron needs glasses. Further
assume that the Compton wave length is much smaller than the size over
which the nuclear potential is smoothed out. In that case, the
potential within a Compton wave length can be approximated by a second
order Taylor series, and the diffusion of it over the Compton wave
length will produce an error proportional to the Laplacian of the
potential (the only fully symmetric combination of derivatives in the
second order Taylor series.). Now if the potential is smoothed over
the nuclear region, its Laplacian, giving the charge density, is known
to produce a nonzero spike only within that smoothed nuclear region,
figure 13.7 or (13.30). Since the nuclear size
is small compared to the electron wave functions, that spike can then
be approximated as a delta function. Tell all your friends you heard
it here first.
The key question is now what are the changes in the hydrogen energy
levels due to the three perturbations discussed above. That can be
answered by perturbation theory as soon as the good eigenfunctions
have been identified. Recall that the usual hydrogen energy
eigenfunctions 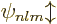 are made unique by the square angular
momentum operator
are made unique by the square angular
momentum operator 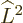 , giving
, giving  , the
, the  angular
momentum operator
angular
momentum operator  , giving
, giving  , and the spin angular
momentum operator
, and the spin angular
momentum operator  giving the spin quantum number
giving the spin quantum number 

 for spin up, respectively down. The decisive term
whether these are good or not is the spin-orbit interaction. If the
inner product in it is written out, it is
for spin up, respectively down. The decisive term
whether these are good or not is the spin-orbit interaction. If the
inner product in it is written out, it is
The radial factor is no problem; it commutes with every orbital
angular momentum component, since these are purely angular
derivatives, chapter 4.2.2. It also commutes with every
component of spin because all spatial functions and operators do,
chapter 5.5.3. As far as the dot product is concerned,
it commutes with 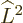 since all the components of
since all the components of 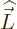 do, chapter
4.5.4, and since all the components of
do, chapter
4.5.4, and since all the components of 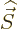 commute with
any spatial operator. But unfortunately,
commute with
any spatial operator. But unfortunately, 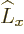 and
and 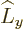 do not
commute with
do not
commute with  , and
, and 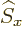 and
and 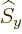 do not commute with
do not commute with
 (chapters 4.5.4 and 5.5.3):
(chapters 4.5.4 and 5.5.3):
The quantum numbers  and
and  are bad.
are bad.
Fortunately,  does commute with the net
does commute with the net  angular
momentum
angular
momentum 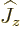 , defined as
, defined as 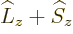 . Indeed, using
the commutators above and the rules of chapter 4.5.4 to
take apart commutators:
. Indeed, using
the commutators above and the rules of chapter 4.5.4 to
take apart commutators:
and adding it all up, you get ![$[{\skew 4\widehat{\vec L}}\cdot{\skew 6\widehat{\vec S}},{\widehat J}_z]$](img5385.gif)
 0. The same
way of course
0. The same
way of course  commutes with the other components of net
angular momentum
commutes with the other components of net
angular momentum 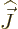 , since the
, since the  -axis is arbitrary. And if
-axis is arbitrary. And if
 commutes with every component of
commutes with every component of 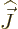 , then it
commutes with their sum of squares
, then it
commutes with their sum of squares  . So, eigenfunctions
of
. So, eigenfunctions
of 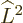 ,
,  , and
, and 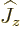 are good
eigenfunctions.
are good
eigenfunctions.
Such good eigenfunctions can be constructed from the 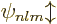 by forming linear combinations of them that combine different
by forming linear combinations of them that combine different  and
and
 values. The coefficients of these good combinations are called
Clebsch-Gordan coefficients and are shown for
values. The coefficients of these good combinations are called
Clebsch-Gordan coefficients and are shown for 
 1 and
1 and 
 2 in figure 12.5. Note from this figure that the
quantum number
2 in figure 12.5. Note from this figure that the
quantum number  of net square momentum can only equal
of net square momentum can only equal 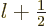 or
or  . The half unit of electron spin is not big
enough to change the quantum number of square orbital momentum by more
than half a unit. For the rest, however, the detailed form of the
good eigenfunctions is of no interest here. They will just be
indicated in ket notation as
. The half unit of electron spin is not big
enough to change the quantum number of square orbital momentum by more
than half a unit. For the rest, however, the detailed form of the
good eigenfunctions is of no interest here. They will just be
indicated in ket notation as 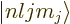 , indicating that
they have unperturbed energy
, indicating that
they have unperturbed energy 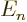 , square orbital angular
momentum
, square orbital angular
momentum  , square net (orbital plus spin) angular
momentum
, square net (orbital plus spin) angular
momentum 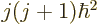 , and net
, and net  angular momentum
angular momentum
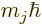 .
.
As far as the other two contributions to the fine structure are
concerned, according to chapter 4.3.1 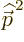 in the
Einstein term consists of radial functions and radial derivatives plus
in the
Einstein term consists of radial functions and radial derivatives plus
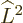 . These commute with the angular derivatives that make up
the components of
. These commute with the angular derivatives that make up
the components of 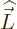 , and as spatial functions and operators,
they commute with the components of spin. So the Einstein Hamiltonian
commutes with all components of
, and as spatial functions and operators,
they commute with the components of spin. So the Einstein Hamiltonian
commutes with all components of 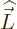 and
and 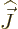

 ,
hence with
,
hence with 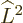 ,
,  , and
, and 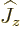 . And the
delta function in the Darwin term can be assumed to be the limit of a
purely radial function and commutes in the same way. The
eigenfunctions
. And the
delta function in the Darwin term can be assumed to be the limit of a
purely radial function and commutes in the same way. The
eigenfunctions 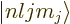 with given values of
with given values of  ,
,
 , and
, and 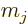 are good ones for the entire fine structure
Hamiltonian.
are good ones for the entire fine structure
Hamiltonian.
To get the energy changes, the Hamiltonian perturbation coefficients
must be found. Starting with the Einstein term, it is
Unlike what you may have read elsewhere, 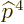 is indeed a
Hermitian operator, but
is indeed a
Hermitian operator, but 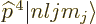 may have a delta
function at the origin, (13.30), so watch it with blindly
applying mathematical manipulations to it. The trick is to take half
of it to the other side of the inner product, and then use the fact
that the eigenfunctions satisfy the nonrelativistic energy eigenvalue
problem:
may have a delta
function at the origin, (13.30), so watch it with blindly
applying mathematical manipulations to it. The trick is to take half
of it to the other side of the inner product, and then use the fact
that the eigenfunctions satisfy the nonrelativistic energy eigenvalue
problem:
Noting from chapter 4.3 that 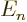

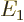

 ,
,


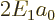

 and that the expectation values of
and that the expectation values of 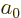

 and
and 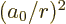 are given in derivation {D.83}, you
find that
are given in derivation {D.83}, you
find that
The spin-orbit energy correction is
For states with no orbital angular momentum, all components of 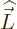 produce zero, so there is no contribution. Otherwise, the dot product
produce zero, so there is no contribution. Otherwise, the dot product
 can be rewritten by expanding
can be rewritten by expanding
to give
That leaves only the expectation value of 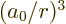 to be
determined, and that can be found in derivation {D.83}. The
net result is
to be
determined, and that can be found in derivation {D.83}. The
net result is
or zero if 
 0.
0.
Finally the Darwin term,
Now a delta function at the origin has the property to pick out the
value at the origin of whatever function it is in an integral with,
compare chapter 7.9.1. Derivation {D.15},
(D.9), implies that the value of the wave functions at the
origin is zero unless 
 0, and then the value is given in
(D.10). So the Darwin contribution becomes
0, and then the value is given in
(D.10). So the Darwin contribution becomes
To get the total energy change due to fine structure, the three
contributions must be added together. For 
 0, add the Einstein and
Darwin terms. For
0, add the Einstein and
Darwin terms. For 
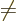 0, add the Einstein and spin-orbit terms;
you will need to do the two possibilities that
0, add the Einstein and spin-orbit terms;
you will need to do the two possibilities that 

 and
and


 separately. All three produce the same final result,
anyway:
separately. All three produce the same final result,
anyway:
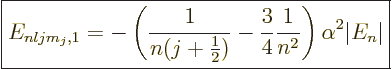 |
(A.252) |
Since 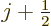 is at most
is at most  , the energy change due to fine
structure is always negative. And it is the biggest fraction of
, the energy change due to fine
structure is always negative. And it is the biggest fraction of 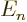 for
for 

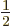 and
and 
 2, where it is
2, where it is
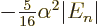 , still no more than a sixth of a
percent of a percent change in energy.
, still no more than a sixth of a
percent of a percent change in energy.
In the ground state  can only be one half, (the electron spin), so
the ground state energy does not split into two due to fine structure.
You would of course not expect so, because in empty space, both spin
directions are equivalent. The ground state does show the largest
absolute change in energy.
can only be one half, (the electron spin), so
the ground state energy does not split into two due to fine structure.
You would of course not expect so, because in empty space, both spin
directions are equivalent. The ground state does show the largest
absolute change in energy.
Woof.
A.39.3 Weak and intermediate Zeeman effect
The weak Zeeman effect is the effect of a magnetic field that is
sufficiently weak that it leaves the fine structure energy
eigenfunctions almost unchanged. The Zeeman effect is then a small
perturbation on a problem in which the unperturbed
(by
the Zeeman effect) eigenfunctions 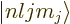 derived in the
previous subsection are degenerate with respect to
derived in the
previous subsection are degenerate with respect to  and
and
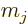 .
.
The Zeeman Hamiltonian
commutes with both 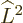 and
and 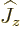

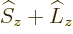 , so the
eigenfunctions
, so the
eigenfunctions 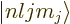 are good. Therefore, the energy
perturbations can be found as
are good. Therefore, the energy
perturbations can be found as
To evaluate this rigorously would require that the 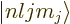 state be converted into the one or two
state be converted into the one or two 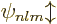 states with
states with





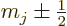

 and
and 

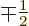 using the appropriate Clebsch-Gordan coefficients from
figure 12.5.
using the appropriate Clebsch-Gordan coefficients from
figure 12.5.
However, the following simplistic derivation is usually given instead,
including in this book. First get rid of 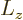 by replacing it by
by replacing it by
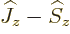 . The inner product with
. The inner product with 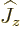 can then be
evaluated as being
can then be
evaluated as being 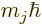 , giving the energy change as
, giving the energy change as
For the final inner product, make a semi-classical argument that only
the component of 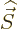 in the direction of
in the direction of  gives a
contribution. Don’t worry that
gives a
contribution. Don’t worry that  does not exist. Just
note that the component in the direction of
does not exist. Just
note that the component in the direction of  is constrained
by the requirement that
is constrained
by the requirement that 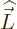 and
and 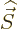 must add up to
must add up to 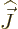 ,
but the component normal to
,
but the component normal to  can be in any direction and
presumably averages out to zero. Dismissing this component, the
component in the direction of
can be in any direction and
presumably averages out to zero. Dismissing this component, the
component in the direction of  is
is
and the dot product in it can be found from expanding
to give
For a given eigenfunction 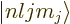 ,
, 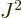

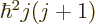 ,
, 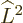

 , and
, and 

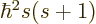 with
with 

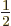 .
.
If the  -component of
-component of 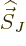 is substituted for
is substituted for  in the
expression for the Hamiltonian perturbation coefficients, the energy
changes are
in the
expression for the Hamiltonian perturbation coefficients, the energy
changes are
![\begin{displaymath}
\left[1+\frac{j(j+1)-l(l+1)+s(s+1)}{2j(j+1)}\right]
\frac{e\hbar}{2m_{\rm e}} {\cal B}_{\rm ext} m_j %
\end{displaymath}](img5424.gif) |
(A.253) |
(Rigorous analysis using figure 12.5, or more generally item
2 in chapter 12.8, produces the same results.)
The factor within the brackets is called the “Landé  -factor.” It is the factor by which the magnetic
moment of the electron in the atom is larger than for a classical
particle with the same charge and total angular momentum. It
generalizes the
-factor.” It is the factor by which the magnetic
moment of the electron in the atom is larger than for a classical
particle with the same charge and total angular momentum. It
generalizes the  -factor of the electron in isolation to include the
effect of orbital angular momentum. Note that it equals 2, the Dirac
-factor of the electron in isolation to include the
effect of orbital angular momentum. Note that it equals 2, the Dirac
 -factor, if there is no orbital momentum, and 1, the classical
value, if the orbital momentum is so large that the half unit of spin
can be ignored.
-factor, if there is no orbital momentum, and 1, the classical
value, if the orbital momentum is so large that the half unit of spin
can be ignored.
In the intermediate Zeeman effect, the fine structure and Zeeman
effects are comparable in size. The dominant perturbation Hamiltonian
is now the combination of the fine structure and Zeeman ones. Since
the Zeeman part does not commute with  , the eigenfunctions
, the eigenfunctions
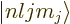 are no longer good. Eigenfunctions with the same
values of
are no longer good. Eigenfunctions with the same
values of  and
and 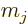 , but different values of
, but different values of  must be
combined into good combinations. For example, if you look at
must be
combined into good combinations. For example, if you look at 
 2, the eigenfunctions
2, the eigenfunctions 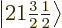 and
and
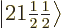 have the same unperturbed energy and good
quantum numbers
have the same unperturbed energy and good
quantum numbers  and
and 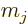 . You will have to write a two by
two matrix of Hamiltonian perturbation coefficients for them, as in
addendum {A.38.3}, to find the good combinations and their
energy changes. And the same for the
. You will have to write a two by
two matrix of Hamiltonian perturbation coefficients for them, as in
addendum {A.38.3}, to find the good combinations and their
energy changes. And the same for the ![${\left\vert 21{\textstyle\frac{3}{2}}\rule[2.5pt]{5pt}{.5pt}{\textstyle\frac{1}{2}}\right\rangle}$](img5427.gif) and
and ![${\left\vert 21{\textstyle\frac{1}{2}}\rule[2.5pt]{5pt}{.5pt}{\textstyle\frac{1}{2}}\right\rangle}$](img5428.gif) eigenfunctions. To obtain the
matrix coefficients, use the Clebsch-Gordan coefficients from figure
12.5 to evaluate the effect of the Zeeman part. The fine
structure contributions to the matrices are given by (A.252)
when the
eigenfunctions. To obtain the
matrix coefficients, use the Clebsch-Gordan coefficients from figure
12.5 to evaluate the effect of the Zeeman part. The fine
structure contributions to the matrices are given by (A.252)
when the  values are equal, and zero otherwise. This can be seen
from the fact that the energy changes must be the fine structure ones
when there is no magnetic field; note that
values are equal, and zero otherwise. This can be seen
from the fact that the energy changes must be the fine structure ones
when there is no magnetic field; note that  is a good quantum
number for the fine structure part, so its perturbation coefficients
involving different
is a good quantum
number for the fine structure part, so its perturbation coefficients
involving different  values are zero.
values are zero.
A.39.4 Lamb shift
A famous experiment by Lamb & Retherford in 1947 showed that the
hydrogen atom state 
 2,
2, 
 0,
0, 

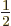 , also called the 2S
, also called the 2S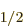 state, has a somewhat different
energy than the state
state, has a somewhat different
energy than the state 
 2,
2, 
 1,
1, 

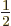 , also called the 2P
, also called the 2P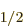 state. That was
unexpected, because even allowing for the relativistic fine structure
correction, states with the same principal quantum number
state. That was
unexpected, because even allowing for the relativistic fine structure
correction, states with the same principal quantum number  and same
total angular momentum quantum number
and same
total angular momentum quantum number  should have the same energy.
The difference in orbital angular momentum quantum number
should have the same energy.
The difference in orbital angular momentum quantum number  should
not affect the energy.
should
not affect the energy.
The cause of the unexpected energy difference is called Lamb shift.
To explain why it occurs would require quantum electrodynamics, and
that is well beyond the scope of this book. Roughly speaking, the
effect is due to a variety of interactions with virtual photons and
electron/positron pairs. A good qualitative discussion on a
nontechnical level is given by Feynman [19].
Here it must suffice to list the approximate energy corrections
involved. For states with zero orbital angular momentum, the energy
change due to Lamb shift is
 |
(A.254) |
where 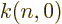 is a numerical factor that varies a bit with
is a numerical factor that varies a bit with  from
about 12.7 to 13.2. For states with nonzero orbital angular momentum,
from
about 12.7 to 13.2. For states with nonzero orbital angular momentum,
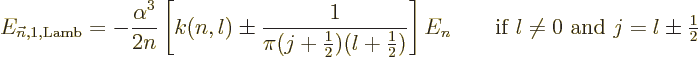 |
(A.255) |
where 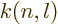 is less than 0.05 and varies somewhat with
is less than 0.05 and varies somewhat with  and
and
 .
.
It follows that the energy change is really small for states with
nonzero orbital angular momentum, which includes the 2P state. The change is biggest for the 2S
state. The change is biggest for the 2S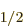 state, the
other state in the Lamb & Retherford experiment. (True, the
correction would be bigger still for the ground state
state, the
other state in the Lamb & Retherford experiment. (True, the
correction would be bigger still for the ground state 
 1, but
since there are no states with nonzero angular momentum in the ground
state, there is no splitting of spectral lines involved there.)
1, but
since there are no states with nonzero angular momentum in the ground
state, there is no splitting of spectral lines involved there.)
Qualitatively, the reason that the Lamb shift is small for states with
nonzero angular momentum has to do with distance from the nucleus.
The nontrivial effects of the cloud of virtual particles around the
electron are most pronounced in the strong electric field very close
to the nucleus. In states of nonzero angular momentum, the wave
function is zero at the nucleus, (D.9). So in those states
the electron is unlikely to be found very close to the nucleus. In
states of zero angular momentum, the square magnitude of the wave
function is 1
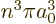 at the nucleus, reflected in both the
much larger Lamb shift as well as its approximate 1
at the nucleus, reflected in both the
much larger Lamb shift as well as its approximate 1
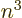 dependence
on the principal quantum number
dependence
on the principal quantum number  .
.
A.39.5 Hyperfine splitting
Hyperfine splitting of the hydrogen atom energy levels is due to the
fact that the nucleus acts as a little magnet just like the electron.
The single-proton nucleus and electron have magnetic dipole moments
due to their spin equal to
in which the  -factor of the proton is about 5.59 and that of the
electron 2. The magnetic moment of the nucleus is much less than the
one of the electron, since the much greater proton mass appears in the
denominator. That makes the energy changes associated with hyperfine
splitting really small compared to other effects such as fine
structure.
-factor of the proton is about 5.59 and that of the
electron 2. The magnetic moment of the nucleus is much less than the
one of the electron, since the much greater proton mass appears in the
denominator. That makes the energy changes associated with hyperfine
splitting really small compared to other effects such as fine
structure.
This discussion will restrict itself to the ground state, which is by
far the most important case. For the ground state, there is no
orbital contribution to the magnetic field of the electron. There is
only a spin-spin coupling
between the magnetic moments
of the electron and proton, The energy involved can be thought of most
simply as the energy 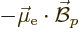 of the electron in the
magnetic field
of the electron in the
magnetic field  of the nucleus. If the nucleus is modelled
as an infinitesimally small electromagnet, its magnetic field is that
of an ideal current dipole as given in table 13.2. The
perturbation Hamiltonian then becomes
of the nucleus. If the nucleus is modelled
as an infinitesimally small electromagnet, its magnetic field is that
of an ideal current dipole as given in table 13.2. The
perturbation Hamiltonian then becomes
The good states are not immediately self-evident, so the four
unperturbed ground states will just be taken to be the ones which the
electron and proton spins combine into the triplet or singlet states
of chapter 5.5.6:
or  for short, where
for short, where
 and
and 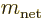 are the quantum numbers of net spin
and its
are the quantum numbers of net spin
and its  -component. The next step is to evaluate the four by four
matrix of Hamiltonian perturbation coefficients
-component. The next step is to evaluate the four by four
matrix of Hamiltonian perturbation coefficients
using these states.
Now the first term in the spin-spin Hamiltonian does not produce a
contribution to the perturbation coefficients. The reason is that the
inner product of the perturbation coefficients written in spherical
coordinates involves an integration over the surfaces of constant
 . The ground state eigenfunction
. The ground state eigenfunction 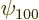 is constant on
these surfaces. So there will be terms like
is constant on
these surfaces. So there will be terms like
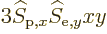 in the integration, and those
are zero because
in the integration, and those
are zero because  is just as much negative as positive on these
spherical surfaces, (as is
is just as much negative as positive on these
spherical surfaces, (as is  ). There will also be terms like
). There will also be terms like
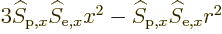 in the integration. These will be zero too because by symmetry the
averages of
in the integration. These will be zero too because by symmetry the
averages of 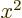 ,
, 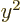 , and
, and 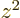 are equal on the
spherical surfaces, each equal to one third the average of
are equal on the
spherical surfaces, each equal to one third the average of
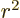 .
.
So only the second term in the Hamiltonian survives, and
the Hamiltonian perturbation coefficients become
The spatial integration in this inner product merely picks out the
value 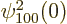
 1
1
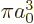 at the origin, as delta functions
do. That leaves the sum over the spin states. According to addendum
{A.10},
at the origin, as delta functions
do. That leaves the sum over the spin states. According to addendum
{A.10},
Since the triplet and singlet spin states are orthonormal, only the
Hamiltonian perturbation coefficients for which


 and
and 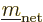

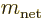 survive, and these then give the leading order changes in the energy.
survive, and these then give the leading order changes in the energy.
Plugging it all in and rewriting in terms of the Bohr energy and fine
structure constant, the energy changes are:
 |
(A.256) |
The energy of the triplet states is raised and that of the singlet
state is lowered. Therefore, in the true ground state, the electron
and proton spins combine into the singlet state. If they somehow get
kicked into a triplet state, they will eventually transition back to
the ground state, say after 10 million years or so, and release a
photon. Since the difference between the two energies is so tiny on
account of the very small values of both 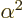 and
and
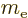

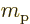 , this will be a very low energy photon. Its wave
length is as long as 0.21 m, producing the 21 cm hydrogen line.
, this will be a very low energy photon. Its wave
length is as long as 0.21 m, producing the 21 cm hydrogen line.
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,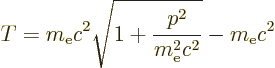
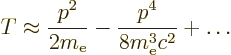
![]() .
.![]()
![]()
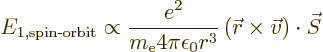
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]() .
.![\begin{eqnarray*}
& & [\L _x{\widehat S}_x,\L _z+{\widehat S}_z] = [\L _x,\L _z...
...,\L _z]{\widehat S}_z + \L _z[{\widehat S}_z,{\widehat S}_z] = 0
\end{eqnarray*}](img5384.gif)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
![]() .
.![]()
![]() .
.![]() ,
,![]()
![]()
![]()
![]() ,
,![]() ,
,![]() ,
,![]() .
.![]()
![]() ,
,![]() ,
,![]()
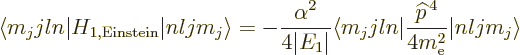
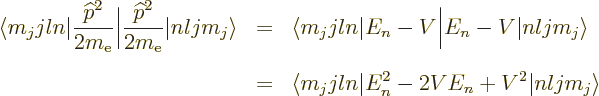
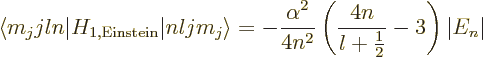
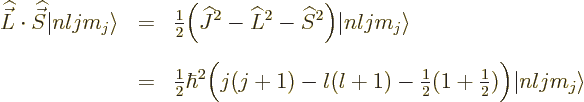
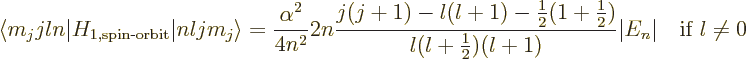
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]() .
.![]()
![]() ,
,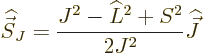
![]() -
-![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.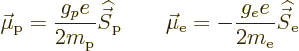
![]()
![]()
![\begin{displaymath}
H_{1,\mbox{\scriptsize spin-spin}} =
\frac{g_{\rm {p}}g_{\...
...dehat{\vec S}}_{\rm {e}})}{3}\delta^3({\skew0\vec r})
\right]
\end{displaymath}](img5438.gif)
![]() .
.![]()
![]()
![]()
![]() )
)![]()
![]() ,
,![]() ,
,![]()
![]() .
.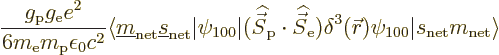
![]()
![]()
![]()
![]()