|
|
|
|
|
Next: D.69 More awkwardness about spin |
|
Now of course you ask: how do you know how the mathematical expressions for spin states change when the coordinate system is rotated around some axis? Darn.
If you did a basic course in linear algebra, they will have told you how the components of normal vectors change when the coordinate system is rotated, but not spin vectors, or spinors, which are two-dimensional vectors in three-dimensional space.
You need to go back to the fundamental meaning of angular momentum.
The effect of rotations of the coordinate system around the
![]() -
-![]() .
.![]()
![]() -
-![]()
![]()
![]() -
-![]()
![]() ,
,
The second term may be compared to the effect of the
![]() -
-![]() ,
,![]() ;
;![]()
![]()
![]() .
.![]()
![]() -
-
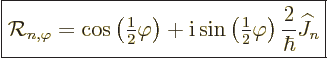 |
(D.44) |
Further, in terms of the ![]() ,
,![]() ,
,![]()
![]() -
-
Using this operator, you can find out how the spin-up and spin-down
states are described in terms of correspondingly defined basis states
along the ![]() -
-![]() -
-![]()
Note however that the very idea of defining the positive ![]()
![]()
![]()
![]()
![]()
![]() 1
1![]() 1
1
More awkwardly, the negative momentum states obtained by rotation do not lead to real positive numerical factors for the corresponding ladder operators. Presumably, this reflects the fact that at the wave function level, nature does not have the rotational symmetry that it has for observable quantities. Anyway, if nature does not bother to obey such symmetry, then there seems no point in pretending it does. Especially since the nonpositive ladder factors would mess up various formulae. The negative spin states found by rotation go out of the window. Bye, bye.