| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
D.78 Shell model quadrupole moment
The result for one proton is readily available in literature and messy
to derive yourself. If you want to give it a try anyway, one way is
the following. Note that in spherical coordinates
and the first term produces 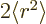 simply by the
definition of expectation value. The problem is to get rid of the
simply by the
definition of expectation value. The problem is to get rid of the
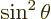 in the second expectation value.
in the second expectation value.
To do so, use chapter 12.8, 2. That shows
that the second term is essentially 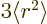 modified by factors of the form
modified by factors of the form
where the integration is over the unit sphere. If you use the
representation of the spherical harmonics as given in
{D.64}, you can relate these inner products to the unit
inner products
Have fun.
The expression for the quadrupole moment if there are an odd number

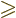 3 of protons in the shell would seem to be a very messy
exercise. Some text books suggest that the odd-particle shell model
implies that the one-proton value applies for any odd number of
protons in the shell. However, it is clear from the state with a
single hole that this is untrue. The cited result that the quadrupole
moment varies linearly with the odd number of protons in the shell
comes directly from Krane, [31, p. 129]. No derivation or
reference is given. In fact, the restriction to an odd number of
protons is not even stated. If you have a reference or a simple
derivation, let me know and I will add it here.
3 of protons in the shell would seem to be a very messy
exercise. Some text books suggest that the odd-particle shell model
implies that the one-proton value applies for any odd number of
protons in the shell. However, it is clear from the state with a
single hole that this is untrue. The cited result that the quadrupole
moment varies linearly with the odd number of protons in the shell
comes directly from Krane, [31, p. 129]. No derivation or
reference is given. In fact, the restriction to an odd number of
protons is not even stated. If you have a reference or a simple
derivation, let me know and I will add it here.
![]()
![]()
![]()