|
|
|
|
|
Next: D.5 Lorentz group property derivation |
|
This note derives the Lorentz transformation as discussed in chapter
1.2. The question is what is the relationship between
the time and spatial coordinates
![]()
![]()
Note that since the choices what to define as time zero and as the
origin are quite arbitrary, it can be arranged that
![]()
![]()
![]()
It will further be assumed that the relationship between the
coordinates is linear;
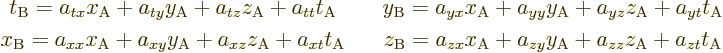
The biggest reason to assume that the transformation should be linear
is that if space is populated with observers A and B, rather than just
have a single one sitting at the origin of that coordinate system,
then a linear transformation assures that all pairs of observers A and
B see the exact same transformation. In addition, the transformation
from ![]()
![]()
Another way to look at it is to say that the spatial and temporal scales seen by normal observers are miniscule compared to the scales of the universe. Based on that idea you would expect that the relation between their coordinates would be a linearized Taylor series.
A lot of additional constraints can be put in because of physical
symmetries that surely still apply even allowing for relativity. For
example, the transformation to ![]()
![]()
![]()
![]()
![]()
![]() -
-![]()
![]()
![]()
![]() .
.![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
You might be able to think up some more constraints, but this will do.
Put it all together to get
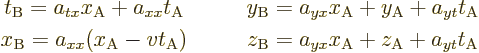
Next the trick is to consider the wave front emitted by some light
source that flashes at time zero at the then coinciding origins.
Since according to the principle of relativity the two coordinate
systems are fully equivalent, in both coordinate systems the wave
front forms an expanding spherical shell with radius ![]() :
:
To derive the given transformations between the velocities seen in the two systems, take differentials of the Lorentz transformation formulae. Then take ratios of the corresponding infinitesimal position increments over the corresponding time increments.