| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
Subsections
1.2 The Lorentz Transformation
The Lorentz transformation
describes how measurements
of the position and time of events change from one observer to the
next. It includes Lorentz-Fitzgerald contraction and time dilation as
special cases.
1.2.1 The transformation formulae
This subsection explains how the position and time coordinates of
events differ from one observer to the next.
Figure 1.2:
Coordinate systems for the Lorentz transformation.
![\begin{figure}\centering
\setlength{\unitlength}{1pt}
\begin{picture}(405,11...
...B}}$}}
\put(254,2){\makebox(0,0)[b]{$z_{\rm {B}}$}}
\end{picture}
\end{figure}](img44.gif) |
Consider two observers A and B that are in motion compared to each
other with a relative speed  . To make things as simple as
possible, it will be assumed that the relative motion is along the
line through the two observers,
. To make things as simple as
possible, it will be assumed that the relative motion is along the
line through the two observers,
As the left side of figure 1.2 shows, observer A can
believe herself to be at rest and see observer B moving away from her
at speed  ; similarly, observer B can believe himself to be at rest
and see observer A moving away from him at speed
; similarly, observer B can believe himself to be at rest
and see observer A moving away from him at speed  , as in the right
side of the figure. The principle of relativity says that both views
are equally valid; there is no physical measurement that can find a
fundamental difference between the two observers. That implies that
both observers must agree on the same magnitude of the relative
velocity
, as in the right
side of the figure. The principle of relativity says that both views
are equally valid; there is no physical measurement that can find a
fundamental difference between the two observers. That implies that
both observers must agree on the same magnitude of the relative
velocity  between them. And it implies that they need to agree on
the speed
between them. And it implies that they need to agree on
the speed  that light moves.
that light moves.
It will further be assumed that both observers use coordinate systems
with themselves at the origin to describe the locations and times of
events. In addition, they both take their  axes along the line of
their relative motion. They also align their
axes along the line of
their relative motion. They also align their  and
and  axes. And
they both define time to be zero at the instant that they meet.
axes. And
they both define time to be zero at the instant that they meet.
In that case the Lorentz transformation says that the relation between
positions and times of events as perceived by the two observers is,
{D.4}:
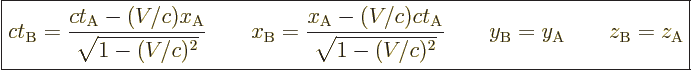 |
(1.6) |
To get the transformation of the coordinates of B into those of A,
just swap A and B and replace  by
by 
 . Indeed, if observer
B is moving in the positive
. Indeed, if observer
B is moving in the positive  -direction with speed
-direction with speed  compared to
observer A, then observer A is moving in the negative
compared to
observer A, then observer A is moving in the negative  -direction
with speed
-direction
with speed  compared to observer B, as in figure 1.2.
In the limit that the speed of light
compared to observer B, as in figure 1.2.
In the limit that the speed of light  becomes infinite, the Lorentz
transformation becomes the nonrelativistic “Galilean transformation” in which
becomes infinite, the Lorentz
transformation becomes the nonrelativistic “Galilean transformation” in which 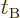 is simply
is simply
 and
and 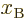

 ,
i.e.
,
i.e. 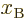 equals
equals 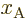 except for a shift of magnitude
except for a shift of magnitude
 .
.
The made assumptions are that A and B are at the origin of their
coordinate system. And that their spatial coordinate systems are
aligned. And that their relative motion is along the  axes. And
that they take the zero of time to be the instant that they meet.
These simplifying assumptions may look very restrictive. But they are
not. A different observer A' at rest relative to A can still use any
coordinate system he wants, with any arbitrary orientation, origin,
and zero of time. Since A' is at rest relative to A, the two
fundamentally agree about space and time. So whatever coordinates and
times A' uses for events are easily converted to those that A uses in
the classical way, {A.3}. Similarly an observer B'
at rest compared to B can still use any arbitrary coordinate system
that she wants. The coordinates and times of events observed by the
arbitrary observers A' and B' can then be related to each other in
stages. First relate the coordinates of A' to those of A in the
classical way. Next use the Lorentz transformation as given above to
relate those to the coordinates of B. Then relate those in the
classical way to the coordinates of B'. In this way, the coordinates
and times of any two observers in relative motion to each other, using
arbitrary coordinate systems and zeros of time, can be related. The
simple Lorentz transformation above describes the nontrivial
part of how the observations of different observers relate.
axes. And
that they take the zero of time to be the instant that they meet.
These simplifying assumptions may look very restrictive. But they are
not. A different observer A' at rest relative to A can still use any
coordinate system he wants, with any arbitrary orientation, origin,
and zero of time. Since A' is at rest relative to A, the two
fundamentally agree about space and time. So whatever coordinates and
times A' uses for events are easily converted to those that A uses in
the classical way, {A.3}. Similarly an observer B'
at rest compared to B can still use any arbitrary coordinate system
that she wants. The coordinates and times of events observed by the
arbitrary observers A' and B' can then be related to each other in
stages. First relate the coordinates of A' to those of A in the
classical way. Next use the Lorentz transformation as given above to
relate those to the coordinates of B. Then relate those in the
classical way to the coordinates of B'. In this way, the coordinates
and times of any two observers in relative motion to each other, using
arbitrary coordinate systems and zeros of time, can be related. The
simple Lorentz transformation above describes the nontrivial
part of how the observations of different observers relate.
Time dilation is one special case of the Lorentz transformation.
Assume that two events 1 and 2 happen at the same location
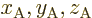 in system A. Then the first
Lorentz transformation formula (1.6) gives
in system A. Then the first
Lorentz transformation formula (1.6) gives
So observer B finds that the time difference between the events is
larger. The same is of course true vice-versa, just use the inverse
formulae.
Lorentz-Fitzgerald contraction is another special case of the Lorentz
transformation. Assume that two stationary locations in system B are
apart by a distance  in the direction of relative
motion. The second Lorentz transformation formula (1.6)
then says how far these points are apart in system A at any given time
in the direction of relative
motion. The second Lorentz transformation formula (1.6)
then says how far these points are apart in system A at any given time
 :
:
Taking the square root to the other side gives the contraction.
As a result of the Lorentz transformation, measured velocities are
related as
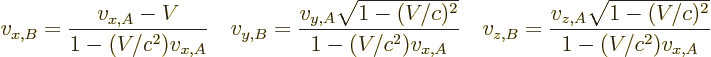 |
(1.7) |
Note that 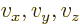 refer here to the perceived velocity
components of some moving object; they are not components of the
velocity difference
refer here to the perceived velocity
components of some moving object; they are not components of the
velocity difference  between the coordinate systems.
between the coordinate systems.
1.2.2 Proper time and distance
In classical Newtonian mechanics, time is absolute. All observers
agree about the difference in time 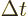 between any two events:
between any two events:
The time difference is an invariant;
it is the same
for all observers.
All observers, regardless of how their spatial coordinate systems are
oriented, also agree over the distance  between two
events that occur at the same time:
between two
events that occur at the same time:
Here the distance between any two points 1 and 2 is found as
The fact that the distance may be expressed as a square root of the
sum of the square components is known as the “Pythagorean theorem.”
Relativity messes all these things up big time. As time dilation
shows, the time between events now depends on who is doing the
observing. And as Lorentz-Fitzgerald contraction shows, distances now
depend on who is doing the observing. For example, consider a moving
ticking clock. Not only do different observers disagree over the
distance  traveled between ticks, (as they would do
nonrelativistically), but they also disagree about the time difference
traveled between ticks, (as they would do
nonrelativistically), but they also disagree about the time difference
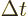 between ticks, (which they would not do
nonrelativistically).
between ticks, (which they would not do
nonrelativistically).
However, there is one thing that all observers can agree on. They do
agree on how much time between ticks an observer moving along with the
clock would measure. That time difference is called the “proper time” difference. (The word proper is a wrongly
translated French propre,
which here means
own.
So proper time really means the clock’s own
time.) The time difference 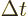 that an observer actually
perceives is longer than the proper time difference
that an observer actually
perceives is longer than the proper time difference  due
to the time dilation:
due
to the time dilation:
Here 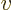 is the velocity of the clock as perceived by the observer.
is the velocity of the clock as perceived by the observer.
To clean this up, take the square root to the other side and write 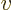 as the distance
as the distance  traveled by the clock divided by
traveled by the clock divided by
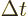 . That gives the proper time difference
. That gives the proper time difference
 between two events, like the ticks of a clock here, as
between two events, like the ticks of a clock here, as
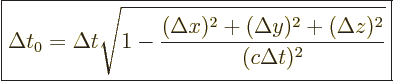 |
(1.8) |
The numerator in the ratio is the square of the distance between the
events.
Note however that the proper time difference is imaginary if the
quantity under the square root is negative. For example, if an
observer perceives two events as happening simultaneously at two
different locations, then the proper time difference between those two
events is imaginary. To avoid dealing with complex numbers, it is
then more convenient to define the “proper distance” 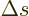 between the two events as
between the two events as
 |
(1.9) |
Note that this is the ordinary distance between the two events if they
are at the same time, i.e. 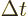
 0. The proper distance
is different from the proper time difference by a factor
0. The proper distance
is different from the proper time difference by a factor
 . Because of the minus sign under the square root,
this factor is imaginary. As a result,
. Because of the minus sign under the square root,
this factor is imaginary. As a result, 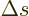 is imaginary if
is imaginary if
 is real and vice-versa.
is real and vice-versa.
All observers agree about the values of the proper time difference
 and the proper distance
and the proper distance 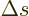 for any two given
events.
for any two given
events.
Physicists define the square of the proper distance to be the
“space-time interval”  . The term is obviously
confusing, as a dictionary defines an interval as a difference in time
or space, not as the square of such a difference. To add more
confusion, some physicists change sign in the definition, and others
divide by the square speed of light. And some rightly define the
interval to be
. The term is obviously
confusing, as a dictionary defines an interval as a difference in time
or space, not as the square of such a difference. To add more
confusion, some physicists change sign in the definition, and others
divide by the square speed of light. And some rightly define the
interval to be 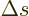 without the square, unfortunately causing
still more confusion.
without the square, unfortunately causing
still more confusion.
If the interval, defined as 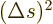 , is positive, then
the proper distance
, is positive, then
the proper distance 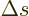 between the two events is real. Such
an interval is called “space-like.” On the other hand, if the interval is negative,
then the proper distance is imaginary. In that case it is the proper
time difference between the events that is real. Such an interval is
called “time-like.”
between the two events is real. Such
an interval is called “space-like.” On the other hand, if the interval is negative,
then the proper distance is imaginary. In that case it is the proper
time difference between the events that is real. Such an interval is
called “time-like.”
If the proper time difference is real, the earlier event can affect,
or even cause, the later event. If the proper time difference is
imaginary however, then the effects of either event cannot reach the
other event even if traveling at the speed of light. It follows that
the sign of the interval is directly related to “causality,” to what can cause what. Since all observers agree
about the value of the proper time difference, they all agree about
what can cause what.
For small differences in time and location, all differences  above become differentials
above become differentials 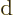 .
.
1.2.3 Subluminal and superluminal effects
Suppose you stepped off the curb at the wrong moment and are now in
the hospital. The pain is agonizing, so you contact one of the
telecommunications microchips buzzing in the sky overhead. These
chips are capable of sending out a “superluminal” beam; a beam that propagates with a speed greater
than the speed of light. The factor with which the speed of the beam
exceeds the speed of light is called the “warp factor” 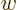 . A beam with a high warp factor is
great for rapid communication with space ships at distant locations in
the solar system and beyond. A beam with a warp factor of 10 allows
ten times quicker communication than those old-fashioned radio waves
that propagate at the speed of light. And these chips have other very
helpful uses, like for your predicament.
. A beam with a high warp factor is
great for rapid communication with space ships at distant locations in
the solar system and beyond. A beam with a warp factor of 10 allows
ten times quicker communication than those old-fashioned radio waves
that propagate at the speed of light. And these chips have other very
helpful uses, like for your predicament.
You select a microchip that is moving at high speed away from the
location where the accident occurred. The microchip sends out its
superluminal beam. In its coordinate system, the beam reaches the
location of the accident at a time 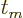 , at which time the beam
has traveled a distance
, at which time the beam
has traveled a distance  equal to
equal to 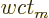 . According to
the Lorentz transformation (1.6), in the coordinate system
fixed to the earth, the beam reaches the location of the accident at a
position and time equal to
. According to
the Lorentz transformation (1.6), in the coordinate system
fixed to the earth, the beam reaches the location of the accident at a
position and time equal to
Because of the high speed  of the microchip and the additional warp
factor, the time that the beam reaches the location of the accident is
negative; the beam has entered into the past. Not far enough in the
past however, so another microchip picks up the message and beams it
back, achieving another reduction in time. After a few more bounces,
the message is beamed to your cell phone. It reaches you just when
you are about to step off the curb. The message will warn you of the
approaching car, but it is not really needed. The mere distraction of
your buzzing cell phone causes you to pause for just a second, and the
car rushes past safely. So the accident never happens; you are no
longer in agony in the hospital, but on your Bermuda vacation as
planned. And these microchips are great for investing in the stock
market too.
of the microchip and the additional warp
factor, the time that the beam reaches the location of the accident is
negative; the beam has entered into the past. Not far enough in the
past however, so another microchip picks up the message and beams it
back, achieving another reduction in time. After a few more bounces,
the message is beamed to your cell phone. It reaches you just when
you are about to step off the curb. The message will warn you of the
approaching car, but it is not really needed. The mere distraction of
your buzzing cell phone causes you to pause for just a second, and the
car rushes past safely. So the accident never happens; you are no
longer in agony in the hospital, but on your Bermuda vacation as
planned. And these microchips are great for investing in the stock
market too.
Sounds good, does it not? Unfortunately, there is a hitch.
Physicists refuse to work on the underlying physics to enable this
technology. They claim it will not be workable, since it will force
them to think up answers to tough questions like: “if you did
not end up in the hospital after all, then why did you still send the
message?” Until they change their mind, our reality will be
that observable matter or radiation cannot propagate faster than the
speed of light.
Therefore, manipulating the past is not possible. An event can only
affect later events. Even more specifically, an event can only affect
a later event if the location of that later event is sufficiently
close that it can be reached with a speed of no more than the speed of
light. A look at the definition of the proper time interval then
shows that this means that the proper time interval between the events
must be real, or time-like.
And while different
observers may disagree about the location and time of the events, they
all agree about the proper time interval. So all observers,
regardless of their velocity, agree on whether an event can affect
another event. And they also all agree on which event is the earlier
one, because before the time interval 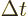 could change sign
for some observer speeds, it would have to pass through zero. It
cannot, because it must be the same for all observers. Relativity
maintains a single reality, even though observers may disagree about
precise times and locations.
could change sign
for some observer speeds, it would have to pass through zero. It
cannot, because it must be the same for all observers. Relativity
maintains a single reality, even though observers may disagree about
precise times and locations.
A more visual interpretation of those concepts can also be given.
Imagine a hypothetical spherical wave front spreading out from the
earlier event with the speed of light. Then a later event can be
affected by the earlier event only if that later event is within or on
that spherical wave front. If you restrict attention to events in the
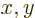 plane, you can use the
plane, you can use the  -coordinate to plot the values of
time. In such a plot, the expanding circular wave front becomes a
cone, called the “light-cone.” Only events within this light cone can be
affected. Similarly in three dimensions and time, an event can only
be affected if it is within the light cone in four-dimensional
space-time. But of course, a cone in four dimensions is hard to
visualize geometrically.
-coordinate to plot the values of
time. In such a plot, the expanding circular wave front becomes a
cone, called the “light-cone.” Only events within this light cone can be
affected. Similarly in three dimensions and time, an event can only
be affected if it is within the light cone in four-dimensional
space-time. But of course, a cone in four dimensions is hard to
visualize geometrically.
1.2.4 Four-vectors
The Lorentz transformation mixes up the space and time coordinates
badly. In relativity, it is therefore best to think of the spatial
coordinates and time as coordinates in a four-dimensional “space-time.”
Since you would surely like all components in a vector to have the
same units, you probably want to multiply time by the speed of light,
because  has units of length. So the four-dimensional “position
vector” can logically be defined to be
has units of length. So the four-dimensional “position
vector” can logically be defined to be 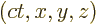 ;
;  is the
is the zeroth
component of the vector where  ,
,
 , and
, and  are components number 1, 2, and 3 as usual. This
four-dimensional position vector will be indicated by
are components number 1, 2, and 3 as usual. This
four-dimensional position vector will be indicated by
![\begin{displaymath}
\kern-1pt{\buildrel\raisebox{-1.5pt}[0pt][0pt]
{\hbox{\hspa...
... \left(\begin{array}{c}r_0\\ r_1\\ r_2\\ r_3\end{array}\right)
\end{displaymath}](img82.gif) |
(1.10) |
The hook on the arrow indicates that time has been hooked into it.
How about the important dot product between vectors? In three
dimensional space this produces such important quantities as the
length of vectors and the angle between vectors. Moreover, the dot
product between two vectors is the same regardless of the orientation
of the coordinate system in which it is viewed.
It turns out that the proper way to define the dot product for
four-vectors reverses the sign of the contribution of the time
components:
![\begin{displaymath}
\kern-1pt{\buildrel\raisebox{-1.5pt}[0pt][0pt]
{\hbox{\hspa...
...
\kern-1.3pt_2 \equiv -c^2t_1t_2 + x_1 x_2 + y_1 y_2 + z_1 z_2
\end{displaymath}](img83.gif) |
(1.11) |
It can be checked by simple substitution that the Lorentz
transformation (1.6) preserves this dot product. In more
expensive words, this inner product
is
invariant under the Lorentz transformation.
Different
observers may disagree about the individual components of
four-vectors, but not about their dot products.
The difference between the four-vector positions of two events has a
proper length
equal to the proper distance between the
events
 |
(1.12) |
So, the fact that all observers agree about proper distance can be
seen as a consequence of the fact that they all agree about dot
products.
It should be pointed out that many physicist reverse the sign of the
spatial components instead of the time in their inner product.
Obviously, this is completely inconsistent with the nonrelativistic
analysis, which is often still a valid approximation. And this
inconsistent sign convention seems to be becoming the dominant one
too. Count on physicists to argue for more than a century about a
sign convention and end up getting it all wrong in the end. One very
notable exception is [49]; you can see why he would end up
with a Nobel Prize in physics.
Some physicists also like to point out that if time is replaced by
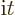 , then the above dot product becomes the normal one.
The Lorentz transformation can then be considered as a mere rotation
of the coordinate system in this four-dimensional space-time. Gee, thanks
physicists! This will be very helpful when examining what happens in
universes in which time is imaginary, unlike our own universe, in
which it is real. The good thing you can say about these physicists
is that they define the dot product the right way: the
, then the above dot product becomes the normal one.
The Lorentz transformation can then be considered as a mere rotation
of the coordinate system in this four-dimensional space-time. Gee, thanks
physicists! This will be very helpful when examining what happens in
universes in which time is imaginary, unlike our own universe, in
which it is real. The good thing you can say about these physicists
is that they define the dot product the right way: the 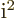 takes
care of the minus sign on the zeroth component.
takes
care of the minus sign on the zeroth component.
Returning to our own universe, the proper length of a four-vector can
be imaginary, and a zero proper length does not imply that the
four-vector is zero as it does in normal three-dimensional space. In fact,
a zero proper length merely indicates that it requires motion at the
speed of light to go from the start point of the four-vector to its
end point.
1.2.5 Index notation
The notations used in the previous subsection are not standard. In
literature, you will almost invariably find the four-vectors and the
Lorentz transform written out in index notation. Fortunately, it does
not require courses in linear algebra and tensor algebra to make some
basic sense out of it.
First of all, in the nonrelativistic case position vectors are
normally indicated by  . The three components of this
vector are commonly indicated by
. The three components of this
vector are commonly indicated by  ,
,  , and
, and  ,
or using indices, by
,
or using indices, by  ,
, 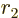 , and
, and 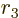 . To
handle space-time, physicists do not simply add a zeroth component
. To
handle space-time, physicists do not simply add a zeroth component
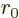 equal to
equal to  . That would make the meaning too easy to
guess. Instead physicists like to indicate the components of
four-vectors by
. That would make the meaning too easy to
guess. Instead physicists like to indicate the components of
four-vectors by 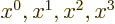 . It is harder to guess
correctly what that means, especially since the letter
. It is harder to guess
correctly what that means, especially since the letter  is already
greatly over-used as it is. A generic component may be denoted as
is already
greatly over-used as it is. A generic component may be denoted as
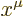 . An entire four-vector can then be indicated by
. An entire four-vector can then be indicated by
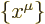 where the brackets indicate the set of all four
components. Needless to say, most physicists forget about the
brackets, because using a component where a vector is required can
have hilarious consequences.
where the brackets indicate the set of all four
components. Needless to say, most physicists forget about the
brackets, because using a component where a vector is required can
have hilarious consequences.
In short,
shows this book’s common sense notation to the left and the index
notation commonly used in physics to the right.
Recall now the Lorentz transformation (1.6). It described
the relationship between the positions and times of events as observed
by two different observers A and B. These observers were in motion
compared to each other with a relative speed  . Physicists
like to put the coefficients of such a Lorentz transformation into a
table, as follows:
. Physicists
like to put the coefficients of such a Lorentz transformation into a
table, as follows:
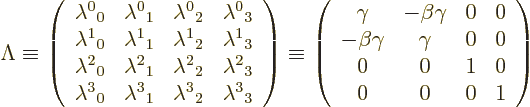 |
(1.13) |
where
A table like 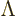 is called a
is called a matrix
or
second-order tensor.
The individual entries in the
matrix are indicated by 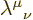 where
where  is the number
of the row and
is the number
of the row and  the number of the column. Note also the
convention of showing the first index as a superscript. That is a
tensor algebra convention. In linear algebra, you normally make all
indices subscripts.
the number of the column. Note also the
convention of showing the first index as a superscript. That is a
tensor algebra convention. In linear algebra, you normally make all
indices subscripts.
(Different sources use different letters for the Lorentz matrix and
its entries. Some common examples are  and
and
 . The name
. The name Lorentz
starts with L
and the Greek letter for L is 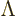 . And Lorentz was Dutch,
which makes him a European just like the Greek. Therefore
. And Lorentz was Dutch,
which makes him a European just like the Greek. Therefore 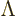 is a good choice for the name of the Lorentz matrix, and
is a good choice for the name of the Lorentz matrix, and 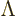 or
lower case
or
lower case 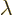 for the entries of the matrix. An
for the entries of the matrix. An  for the
matrix and
for the
matrix and  for its entries would be just too easy to guess. Also,
for its entries would be just too easy to guess. Also,
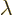 is the standard name for the eigenvalues of matrices and
is the standard name for the eigenvalues of matrices and
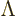 for the matrix of those eigenvalues. So there is some
potential for hilarious confusion there. An
for the matrix of those eigenvalues. So there is some
potential for hilarious confusion there. An a
for the
Lorentz matrix is good too: the name Lorentz
consists
of roman letters and a is the first letter of the roman alphabet.)
The values of the entries 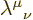 may vary. The ones
shown in the final matrix in (1.13) above apply only in
the simplest nontrivial case. In particular, they require that the
relative motion of the observers is aligned with the
may vary. The ones
shown in the final matrix in (1.13) above apply only in
the simplest nontrivial case. In particular, they require that the
relative motion of the observers is aligned with the  axes as in
figure 1.2. If that is not the case, the values become a
lot more messy.
axes as in
figure 1.2. If that is not the case, the values become a
lot more messy.
In terms of the above notations, the Lorentz transformation
(1.6) can be written as
That is obviously a lot more concise than (1.6). Some
further shorthand notation is now used. In particular, the “Einstein summation convention” is to leave away the summation
symbol  . So, you will likely find the Lorentz
transformation written more concisely as
. So, you will likely find the Lorentz
transformation written more concisely as
Whenever an index like  appears twice in an expression, summation
over that index is to be understood. In other words, you yourself are
supposed to mentally add back the missing summation over all four
values of
appears twice in an expression, summation
over that index is to be understood. In other words, you yourself are
supposed to mentally add back the missing summation over all four
values of  to the expression above. Also, if an index appears
only once, like
to the expression above. Also, if an index appears
only once, like  above, it is to be understood that the equation
is valid for all four values of that index.
above, it is to be understood that the equation
is valid for all four values of that index.
It should be noted that mathematicians call the matrix 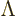 the
transformation matrix from B to A, even though it
produces the coordinates of B from those of A. However,
after you have read some more in this book, insane notation will no
longer surprise you. Just that in this case it comes from
mathematicians.
the
transformation matrix from B to A, even though it
produces the coordinates of B from those of A. However,
after you have read some more in this book, insane notation will no
longer surprise you. Just that in this case it comes from
mathematicians.
In understanding tensor algebra, it is essential to recognize one
thing. It is that a quantity like a position differential transforms
different from a quantity like a gradient:
In the first expression, the partial derivatives are by definition the
entries of the Lorentz matrix 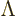 ,
,
In the second expression, the corresponding partial derivatives will
be indicated by
The entries 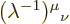 form the so-called
form the so-called
inverse
Lorentz matrix 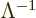 . If the
Lorentz transformation describes a transformation from an observer A
to an observer B, then the inverse transformation describes the
transformation from B to A.
. If the
Lorentz transformation describes a transformation from an observer A
to an observer B, then the inverse transformation describes the
transformation from B to A.
Assuming that the Lorentz transformation matrix is the simple one to
the right in (1.13), the inverse matrix 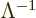 looks exactly the same as
looks exactly the same as  except that
except that 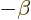 gets replaced
by
gets replaced
by 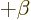 . The reason is fairly simple. The quantity
. The reason is fairly simple. The quantity 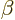 is
the velocity between the observers scaled with the speed of light.
And the relative velocity of B seen by A is the opposite of the one of
A seen by B, if their coordinate systems are aligned.
is
the velocity between the observers scaled with the speed of light.
And the relative velocity of B seen by A is the opposite of the one of
A seen by B, if their coordinate systems are aligned.
Consider now the reason why tensor analysis raises some indices.
Physicists use a superscript index on a vector if it transforms using
the normal Lorentz transformation matrix 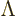 . Such a
vector is called a “contravariant” vector for reasons not worth describing. As an
example, a position differential is a contravariant vector. So the
components of a position differential are indicated by
. Such a
vector is called a “contravariant” vector for reasons not worth describing. As an
example, a position differential is a contravariant vector. So the
components of a position differential are indicated by 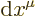 with a superscript index.
with a superscript index.
If a vector transforms using the inverse matrix 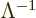 ,
it is called a “covariant” vector. In that case subscript indices are used.
For example, the gradient of a function
,
it is called a “covariant” vector. In that case subscript indices are used.
For example, the gradient of a function  is a covariant vector. So
a component
is a covariant vector. So
a component 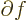

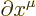 is commonly indicated by
is commonly indicated by
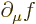 .
.
Now suppose that you flip over the sign of the zeroth, time, component
of a four-vector like a position or a position differential. It turns
out that the resulting four-vector then transforms using the inverse
Lorentz transformation matrix. That means that it has become a
covariant vector. (You can easily verify this in case of the simple
Lorentz transform above.) Therefore lower indices are used for the
flipped-over vector:
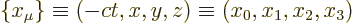
The convention of showing covariant vectors as rows instead of columns
comes from linear algebra. Tensor notation by itself does not have
such a graphical interpretation.
Keep one important thing in mind though. If you flip the sign of a
component of a vector, you get a fundamentally different vector. The
vector  is not just a somewhat different way to
write the position four-vector
is not just a somewhat different way to
write the position four-vector 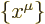 of the space-time point
that you are interested in. Now normally if you define some new
vector that is different from a vector that you are already using, you
change the name. For example, you might change the name from
of the space-time point
that you are interested in. Now normally if you define some new
vector that is different from a vector that you are already using, you
change the name. For example, you might change the name from  to
to
 or to
or to 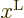 say. Tensor algebra does not do that.
Therefore the golden rule is:
say. Tensor algebra does not do that.
Therefore the golden rule is:
The names of tensors are only correct if the indices are at the
right height.
If you remember that, tensor algebra becomes a lot less confusing.
The expression 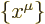 is only your space-time location named
is only your space-time location named  if the index is a superscript as shown. The four-vector
if the index is a superscript as shown. The four-vector  is simply a different animal. How do you know what is the right
height? You just have to remember, you know.
is simply a different animal. How do you know what is the right
height? You just have to remember, you know.
Now consider two different contravariant four-vectors, call them
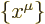 and
and 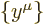 . The dot product between these two
four-vectors can be written as
. The dot product between these two
four-vectors can be written as
To see why, recall that since the index  appears twice, summation
over that index is understood. Also, the lowered index of
appears twice, summation
over that index is understood. Also, the lowered index of 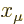 indicates that the sign of the zeroth component is flipped over. That
produces the required minus sign on the product of the time components
in the dot product.
indicates that the sign of the zeroth component is flipped over. That
produces the required minus sign on the product of the time components
in the dot product.
Note also from the above examples that summation indices appear once
as a subscript and once as a superscript. That is characteristic of
tensor algebra.
Addendum {A.4} gives a more extensive description of
the most important tensor algebra formulae for those with a good
knowledge of linear algebra.
1.2.6 Group property
The derivation of the Lorentz transformation as given earlier examined
two observers A and B. But now assume that a third observer C is in
motion compared to observer B. The coordinates of an event as
perceived by observer C may then be computed from those of B using the
corresponding Lorentz transformation, and the coordinates of B may in
turn be computed from those of A using that Lorentz transformation.
Schematically,
But if everything is OK, that means that the Lorentz transformations
from A to B followed by the Lorentz transformation from B to C must be
the same as the Lorentz transformation from A directly to C. In other
words, the combination of two Lorentz transformations must be another
Lorentz transformation.
Mathematicians say that Lorentz transformations must form a
group.
It is much like rotations of a coordinate
system in three spatial dimensions: a rotation followed by another one
is equivalent to a single rotation over some combined angle. In fact,
such spatial rotations are Lorentz transformations; just
between coordinate systems that do not move compared to each other.
Using a lot of linear algebra, it may be verified that indeed the
Lorentz transformations form a group, {D.5}.
![]() .
.![]() ;
;![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
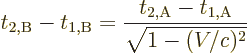
![]()
![]() :
: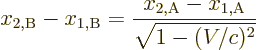
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]() .
.![]()
![]() ,
,![]()
![]()
![]() .
.![]() .
.![]() ,
,![]()
![]() .
.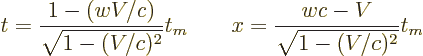
![]()
![]()
![]() -
-![]()
![]() ;
;![]()
![]() ,
,![]() ,
,![]()
![\begin{displaymath}
\kern-1pt{\buildrel\raisebox{-1.5pt}[0pt][0pt]
{\hbox{\hspa...
... \left(\begin{array}{c}r_0\\ r_1\\ r_2\\ r_3\end{array}\right)
\end{displaymath}](img82.gif)
![]() ,
,![]()
![]() .
.![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.![]()
![]() .
.![]() .
.![]()
![]() .
.![]()

![]() .
.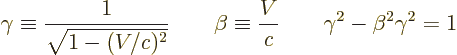
![]()
![]() .
.![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
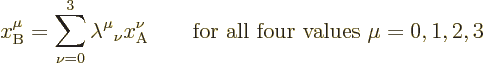
![]()
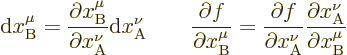

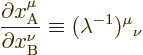
![]()
![]()
![]()
![]() .
.![]()
![]() .
.![]()
![]() ,
,![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.