| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
D.5 Lorentz group property derivation
This note verifies the group property of the Lorentz transformation.
It is not recommended unless you have had a solid course in linear
algebra.
Note first that a much more simple argument can be given by defining
the Lorentz transformation more abstractly, {A.4}
(A.13). But that is cheating. Then you have to prove that
these Lorentz transform are always the same as the physical ones.
For simplicity it will be assumed that the observers still use a
common origin of space and time coordinates.
The group property is easy to verify if the observers B and C are
going in the same direction compared to A. Just multiply two matrices
of the form (1.13) together and apply the condition that
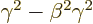
 1 for each.
1 for each.
It gets much messier if the observers move in different directions.
In that case the only immediate simplification that can be made is to
align the coordinate systems so that both relative velocities are in
the 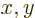 planes. Then the transformations only involve
planes. Then the transformations only involve  in a
trivial way and the combined transformation takes the generic form
in a
trivial way and the combined transformation takes the generic form
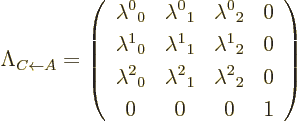
It needs to be shown that this is a Lorentz transformation from A
directly to C.
Now the spatial, 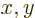 , coordinate system of observer C can be
rotated to eliminate
, coordinate system of observer C can be
rotated to eliminate  and the spatial coordinate system
of observer A can be rotated to eliminate
and the spatial coordinate system
of observer A can be rotated to eliminate 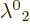 . Next
both Lorentz transformations preserve the inner products. Therefore
the dot product between the four-vectors
. Next
both Lorentz transformations preserve the inner products. Therefore
the dot product between the four-vectors 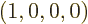 and
and  in the A system must be the same as the dot product between columns 1
and 3 in the matrix above. And that means that
in the A system must be the same as the dot product between columns 1
and 3 in the matrix above. And that means that 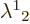 must
be zero, because
must
be zero, because 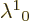 will not be zero except in the
trivial case that systems A and C are at rest compared to each other.
Next since the proper length of the vector
will not be zero except in the
trivial case that systems A and C are at rest compared to each other.
Next since the proper length of the vector  equals one in
the A system, it does so in the C system, so
equals one in
the A system, it does so in the C system, so 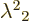 must be
one. (Or minus one, but a 180
must be
one. (Or minus one, but a 180 rotation of the spatial
coordinate system around the
rotation of the spatial
coordinate system around the  -axis can take care of that.) Next,
since the dot product of the vectors
-axis can take care of that.) Next,
since the dot product of the vectors 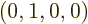 and
and  is
zero, so is
is
zero, so is 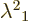 .
.
That leaves the four values relating the time and  components.
From the fact that the dot product of the vectors
components.
From the fact that the dot product of the vectors 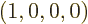 and
and
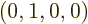 is zero,
is zero,
where 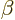 is some constant. Also, since the proper lengths of
these vectors are minus one, respectively one,
is some constant. Also, since the proper lengths of
these vectors are minus one, respectively one,
or substituting in for  and
and 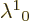 from the above
from the above
It follows that 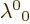 and
and 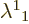 must be equal, (or
opposite, but since both Lorentz transformations have unit
determinant, so must their combination), so call them
must be equal, (or
opposite, but since both Lorentz transformations have unit
determinant, so must their combination), so call them  .
The transformation is then a Lorentz transformation of the usual form
(1.13). (Since the spatial coordinate system cannot just
flip over from left handed to right handed at some point,
.
The transformation is then a Lorentz transformation of the usual form
(1.13). (Since the spatial coordinate system cannot just
flip over from left handed to right handed at some point,  will have to be positive.) Examining the transformation of the origin
will have to be positive.) Examining the transformation of the origin
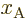

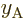

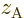
 0 identifies
0 identifies
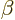 as
as 

 , with
, with  the relative velocity of system A
compared to B, and then the above two equations identify
the relative velocity of system A
compared to B, and then the above two equations identify  as
the Lorentz factor.
as
the Lorentz factor.
Obviously, if any two Lorentz transformations are equivalent to a
single one, then by repeated application any arbitrary number of them
are equivalent to a single one.
![]()
![]()
![]()
![]()
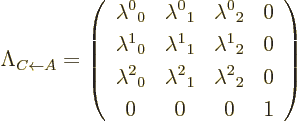
![]() ,
,![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() -
-![]()
![]()
![]() .
.![]()
![]()
![]()
