A.3 Galilean trans­for­ma­tion

The Galilean trans­for­ma­tion de­scribes co­or­di­nate sys­tem trans­for­ma­tions in non­rel­a­tivis­tic New­ton­ian physics. This note ex­plains these trans­for­ma­tion rules. Es­sen­tially the same analy­sis also ap­plies to Lorentz trans­for­ma­tions be­tween ob­servers us­ing ar­bi­trar­ily cho­sen co­or­di­nate sys­tems. The small dif­fer­ence will be in­di­cated.

Con­sider two ob­servers A' and B' that are in in­er­tial mo­tion. In other words, they do not ex­pe­ri­ence ac­cel­er­at­ing forces. The two ob­servers move with a rel­a­tive ve­loc­ity of mag­ni­tude $V$ rel­a­tive to each other. Ob­server A' de­ter­mines the time of events us­ing a suit­able clock. This clock dis­plays the time $t_{\rm {A'}}$ as a sin­gle num­ber, say as the num­ber of sec­onds since a suit­ably cho­sen ref­er­ence event. To spec­ify the po­si­tion of events, ob­server A' uses a Carte­sian co­or­di­nate sys­tem $(x_{\rm {A'}},y_{\rm {A'}},z_{\rm {A'}})$ that is at rest com­pared to him. The ori­gin of the co­or­di­nate sys­tem is cho­sen at a suit­able lo­ca­tion, maybe the lo­ca­tion of the ref­er­ence event that is used as the zero of time.

Ob­server B' de­ter­mines time us­ing a clock that in­di­cates a time $t_{\rm {B'}}$. This time might be zero at a dif­fer­ent ref­er­ence event than the time $t_{\rm {A'}}$. To spec­ify the po­si­tion of events, ob­server B' uses a Carte­sian co­or­di­nate sys­tem $(x_{\rm {B'}},y_{\rm {B'}},z_{\rm {B'}})$ that is at rest com­pared to her. The ori­gin of this co­or­di­nate sys­tem is dif­fer­ent from the one used by ob­server A'. For one, the two ori­gins are in mo­tion com­pared to each other with a rel­a­tive speed $V$.

The ques­tion is now, what is the re­la­tion­ship be­tween the times and po­si­tions that these two ob­servers at­tach to ar­bi­trary events.

To an­swer this, it is con­ve­nient to in­tro­duce two ad­di­tional ob­servers A and B. Ob­server A is at rest com­pared to ob­server A'. How­ever, she takes her zero of time and the ori­gin of her co­or­di­nate sys­tem from ob­server B'. In par­tic­u­lar, the lo­ca­tion and time that A as­so­ciates with her ori­gin at time zero is also the ori­gin at time zero for ob­server B':

$$(x_{\rm {A}},y_{\rm {A}},z_{\rm {A}},t_{\rm {A}}) = (0,0,0,... ...{\rm {B'}},y_{\rm {B'}},z_{\rm {B'}},t_{\rm {B'}}) = (0,0,0,0)$$

The other ad­di­tional ob­server, B, is at rest com­pared to B'. Like ob­server A, ob­server B uses the same ori­gin and zero of time as ob­server B':

$$(x_{\rm {B}},y_{\rm {B}},z_{\rm {B}},t_{\rm {B}}) = (0,0,0,... ...{\rm {B'}},y_{\rm {B'}},z_{\rm {B'}},t_{\rm {B'}}) = (0,0,0,0)$$

Ob­server B ori­ents her co­or­di­nate sys­tem like A does.

That makes the re­la­tion­ship be­tween A and B just like A and B as dis­cussed for the Lorentz trans­form, fig­ure 1.2. How­ever, the clas­si­cal Galilean trans­for­ma­tion is much sim­pler than the Lorentz trans­for­ma­tion. It is

$$\fbox{$\displaystyle t_{\rm{B}} = t_{\rm{A}} \qquad x_{\... ...y_{\rm{B}} = y_{\rm{A}} \qquad z_{\rm{B}} = z_{\rm{A}} $} %$$ (A.11)

Note how­ever that these clas­si­cal for­mu­lae are only an ap­prox­i­ma­tion. They can only be used if the rel­a­tive ve­loc­ity $V$ be­tween the ob­servers is much smaller than the speed of light. In fact, if you take the limit $c\to\infty$ of the Lorentz trans­for­ma­tion (1.6), you get the Galilean trans­for­ma­tion above.

The ques­tion still is how to re­late the times and lo­ca­tions that ob­server A' at­taches to events to those that ob­server B' does. To an­swer that, it is con­ve­nient to do it in stages. First re­late the times and lo­ca­tions that A' at­taches to events to the ones that A does. Then use the for­mu­lae above to re­late the times and lo­ca­tions that A at­taches to events to the ones that B does. Or, if you want the rel­a­tivis­tic trans­for­ma­tion, at this stage use the Lorentz trans­for­ma­tion (1.6). Fi­nally, re­late the times and lo­ca­tions that B at­taches to events to the ones that B' does.

Con­sider then now the re­la­tion­ship be­tween the times and lo­ca­tions that A' at­taches to events and the ones that A does. Since ob­server A and A' are at rest rel­a­tive to each other, they agree about dif­fer­ences in time be­tween events. How­ever, A' uses a dif­fer­ent zero for time. There­fore, the re­la­tion be­tween the times used by the two ob­servers is

$$\fbox{$\displaystyle t_{\rm{A}} = t_{\rm{A'}} - \tau_{\rm{AA'}} $} %$$

Here $\tau_{\rm {AA'}}$ is the time that ob­server A' as­so­ciates with the ref­er­ence event that ob­server A uses as time zero. It is a con­stant, and equal to $-\tau_{\rm {A'A}}$. The lat­ter can be seen by sim­ply set­ting $t_{\rm {A'}}$ zero in the for­mula above.

To spec­ify the lo­ca­tion of events, both ob­servers A' and A use Carte­sian co­or­di­nate sys­tems. Since the two ob­servers are at rest com­pared to each other, they agree on dis­tances be­tween lo­ca­tions. How­ever, their co­or­di­nate sys­tems have dif­fer­ent ori­gins. And they are also ori­ented un­der dif­fer­ent an­gles. That makes the unit vec­tors ${\hat\imath}$, ${\hat\jmath}$, and ${\hat k}$ along the co­or­di­nate axes dif­fer­ent. In vec­tor form the re­la­tion be­tween the co­or­di­nates is then:

$$\fbox{$\displaystyle x_{\rm{A}} {\hat\imath}_{\rm{A}} + y... ...'}} + (z_{\rm{A'}}-\zeta_{\rm{AA'}}) {\hat k}_{\rm{A'}} $} %$$ (A.12)

Here $\xi_{\rm {AA'}}$, $\eta_{\rm {AA'}}$, and $\theta_{\rm {AA'}}$ are the po­si­tion co­or­di­nates that ob­server A' as­so­ciates with the ori­gin of the co­or­di­nate sys­tem of A. By putting $(x_{\rm {A'}},y_{\rm {A'}},z_{\rm {A'}})$ to zero in the ex­pres­sion above, you can re­late this to the co­or­di­nates that A at­taches to the ori­gin of A'.

The above equa­tions can be used to find the co­or­di­nates of A in terms of those of A. To do so, you will need to know the com­po­nents of the unit vec­tors used by A' in terms of those used by A. In other words, you need to know the dot prod­ucts in

$$\begin{eqnarray*} {\hat\imath}_{\rm {A'}} & = & ({\hat\imath}_{\rm {A'}}\cdot{... ... ({\hat k}_{\rm {A'}}\cdot{\hat k}_{\rm {A}}) {\hat k}_{\rm {A}} \end{eqnarray*}$$

Then these re­la­tions al­low you to sum the ${\hat\imath}_{\rm {A}}$ com­po­nents in the right hand side of (A.12) to give $x_{\rm {A}}$. Sim­i­larly the ${\hat\jmath}_{\rm {A}}$ com­po­nents sum to $y_{\rm {A}}$ and the ${\hat k}_{\rm {A}}$ com­po­nents to $z_{\rm {A}}$.

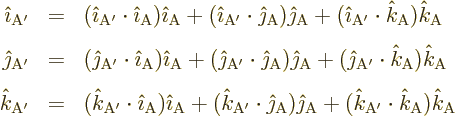
Note also that if you know these dot prod­ucts, you also know the ones for the in­verse trans­for­ma­tion, from A to A'. For ex­am­ple,

$$({\hat\imath}_{\rm {A}}\cdot{\hat\imath}_{\rm {A'}}) = ({\... ...{\rm {A'}}\cdot{\hat\imath}_{\rm {A}}) \qquad \mbox{etcetera}$$

(In terms of lin­ear al­ge­bra, the dot prod­ucts form a 3 $\times$ 3 ma­trix. This ma­trix is called “uni­tary,” or as a real ma­trix also more specif­i­cally “or­tho­nor­mal,” since it pre­serves dis­tances be­tween lo­ca­tions. The ma­trix for the re­verse trans­form is found by tak­ing a trans­pose.)

The re­la­tion­ship be­tween ob­servers B and B' is a sim­pli­fied ver­sion of the one be­tween ob­servers A and A'. It is sim­pler be­cause B and B' use the same zero of time and the same ori­gin. There­fore the for­mu­lae can be ob­tained from the ones given above by re­plac­ing A' and A by B and B' and drop­ping the terms re­lated to time and ori­gin shifts.