| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
A.4 More on index notation
Engineering students are often much more familiar with linear algebra
than with tensor algebra. So it may be worthwhile to look at the
Lorentz transformation from a linear algebra point of view. The
relation to tensor algebra will be indicated. If you do not know
linear algebra, there is little point in reading this addendum.
A contravariant four-vector like position can be pictured as a column
vector that transforms with the Lorentz matrix 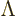 . A
covariant four-vector like the gradient of a scalar function can be
pictured as a row vector that transforms with the inverse Lorentz
matrix
. A
covariant four-vector like the gradient of a scalar function can be
pictured as a row vector that transforms with the inverse Lorentz
matrix 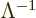 :
:
In linear algebra, a superscript 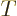 transforms columns into rows and
vice-versa. Since you think of the gradient by itself as a column
vector, the T turns it into a row vector. Note also that putting the
factors in a product in the correct order is essential in linear
algebra. In the second equation above, the gradient, written as a
row, premultiplies the inverse Lorentz matrix.
transforms columns into rows and
vice-versa. Since you think of the gradient by itself as a column
vector, the T turns it into a row vector. Note also that putting the
factors in a product in the correct order is essential in linear
algebra. In the second equation above, the gradient, written as a
row, premultiplies the inverse Lorentz matrix.
In tensor notation, the above expressions are written as
The order of the factors is now no longer a concern; the correct way
of multiplying follows from the names of the indices.
The key property of the Lorentz transformation is that it preserves
dot products. Pretty much everything else follows from that.
Therefore the dot product must now be formulated in terms of linear
algebra. That can be done as follows:
The matrix  is called the “Minkowski metric.” The effect of
is called the “Minkowski metric.” The effect of  on
on ![$\kern-1pt{\buildrel\raisebox{-1.5pt}[0pt][0pt]
{\hbox{\hspace{1pt}$\scriptscriptstyle\hookrightarrow$\hspace{0pt}}}\over r}
\kern-1.3pt_2$](img3648.gif) is to flip
over the sign of the zeroth, time, entry. Looking at it another way,
the effect of
is to flip
over the sign of the zeroth, time, entry. Looking at it another way,
the effect of  on the preceding
on the preceding ![$\kern-1pt{\buildrel\raisebox{-1.5pt}[0pt][0pt]
{\hbox{\hspace{1pt}$\scriptscriptstyle\hookrightarrow$\hspace{0pt}}}\over r}
\kern-1.3pt_1^{\,\rm {T}}$](img3649.gif) is to flip over
the sign of its zeroth entry. Either way,
is to flip over
the sign of its zeroth entry. Either way,  provides the minus sign
for the product of the time coordinates in the dot product.
provides the minus sign
for the product of the time coordinates in the dot product.
In tensor notation, the above expression must be written as
In particular, since space-time positions have superscripts, the
metric matrix  needs to be assigned subscripts. That maintains the
convention that a summation index appears once as a subscript and once
as a superscript.
needs to be assigned subscripts. That maintains the
convention that a summation index appears once as a subscript and once
as a superscript.
Since dot products are invariant,
Here the final equality substituted the Lorentz transformation from A
to B. Recall that if you take a transpose of a product, the order of
the factors gets inverted. If the expression to the far left is
always equal to the one to the far right, it follows that
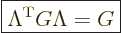 |
(A.13) |
This must be true for any Lorentz transform. In fact, many sources
define Lorentz transforms as transforms that satisfy the above
relationship. Therefore, this relationship will be called the
defining relation.
It is very convenient for doing the
various mathematics. However, this sort of abstract definition does
not really promote easy physical understanding.
And there are a couple of other problems with the defining relation.
For one, it allows Lorentz transforms in which one observer uses a
left-handed coordinate system instead of a right-handed one. Such an
observer observes a mirror image of the universe. Mathematically at
least. A Lorentz transform that switches from a normal right-handed
coordinate system to a left handed one, (or vice-versa), is called
“improper.” The simplest example of such an improper
transformation is 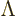


 . That is called the
“parity transformation.” Its effect is to flip over all spatial
position vectors. (If you make a picture of it, you can see that
inverting the directions of the
. That is called the
“parity transformation.” Its effect is to flip over all spatial
position vectors. (If you make a picture of it, you can see that
inverting the directions of the  ,
,  , and
, and  axes of
a right-handed coordinate system produces a left-handed system.) To
see that
axes of
a right-handed coordinate system produces a left-handed system.) To
see that 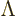


 satisfies the defining relation above,
note that
satisfies the defining relation above,
note that  is symmetric,
is symmetric, 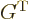

 , and its own
inverse,
, and its own
inverse, 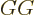

 .
.
Another problem with the defining relation is that it allows one
observer to use an inverted direction of time. Such an observer
observes the universe evolving to smaller values of her time
coordinate. A Lorentz transform that switches the direction of time
from one observer to the next is called “nonorthochronous.” (Ortho indicates correct, and chronous
time.) The simplest example of a nonorthochronous
transformation is 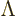

 . That transformation is
called “time-reversal.” Its effect is to simply replace the time
. That transformation is
called “time-reversal.” Its effect is to simply replace the time  by
by

 . It satisfies the defining relation for the same reasons
as the parity transformation.
. It satisfies the defining relation for the same reasons
as the parity transformation.
As a result, there are four types of Lorentz transformations that
satisfy the defining relation. First of all there are the normal
proper orthochronous ones. The simplest example is the unit matrix
 , corresponding to the case that the observers A and B are
identical. Second, there are the improper ones like
, corresponding to the case that the observers A and B are
identical. Second, there are the improper ones like 
 that
switch the handedness of the coordinate system. Third there are the
nonorthochronous ones like
that
switch the handedness of the coordinate system. Third there are the
nonorthochronous ones like  that switch the correct direction of
time. And fourth, there are improper nonorthochronous transforms,
like
that switch the correct direction of
time. And fourth, there are improper nonorthochronous transforms,
like 
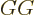


 , that switch both the handedness and
the direction of time.
, that switch both the handedness and
the direction of time.
These four types of Lorentz transforms form four distinct groups. You
cannot gradually change from a right-handed coordinate system to a
left-handed one. Either a coordinate system is right-handed or it is
left-handed. There is nothing in between. By the same token, either
a coordinate system has the proper direction of time or the exactly
opposite direction.
These four groups are reflected in mathematical properties of the
Lorentz transforms. Lorentz transform matrices have determinants that
are either 1 or  1. That is easily seen from taking determinants of
both sides of the defining equation (A.13), splitting the
left determinant in its three separate factors. Also, Lorentz
transforms have values of the entry
1. That is easily seen from taking determinants of
both sides of the defining equation (A.13), splitting the
left determinant in its three separate factors. Also, Lorentz
transforms have values of the entry 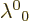 that are either
greater or equal to 1 or less or equal to
that are either
greater or equal to 1 or less or equal to  1. That is readily
seen from writing out the
1. That is readily
seen from writing out the 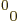 entry of (A.13).
entry of (A.13).
Proper orthochronous Lorentz transforms have a determinant 1 and an
entry 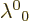 greater or equal to 1. That can readily be
checked for the simplest example
greater or equal to 1. That can readily be
checked for the simplest example 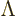

 . More
generally, it can easily be checked that
. More
generally, it can easily be checked that 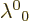 is the time
dilatation factor for events that happen right in the hands of
observer A. That is the physical reason that
is the time
dilatation factor for events that happen right in the hands of
observer A. That is the physical reason that 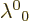 must
always be greater or equal to 1. Transforms that have
must
always be greater or equal to 1. Transforms that have
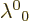 less or equal to
less or equal to  1 flip over the correct direction
of time. So they are nonorthochronous. Transforms that switch over
the handedness of the coordinate system produce a negative
determinant. But so do nonorthochronous transforms. If a transform
flips over both handedness and the direction of time, it has a time
dilatation less or equal to
1 flip over the correct direction
of time. So they are nonorthochronous. Transforms that switch over
the handedness of the coordinate system produce a negative
determinant. But so do nonorthochronous transforms. If a transform
flips over both handedness and the direction of time, it has a time
dilatation less or equal to  1 but a positive determinant.
1 but a positive determinant.
For reasons given above, if you start with some proper orthochronous
Lorentz transform like 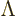

 and gradually change it, it stays
proper and orthochronous. But in addition its determinant stays 1 and
its time-dilatation entry stays greater or equal to 1. The reasons
are essentially the same as before. You cannot gradually change from
a value of 1 or above to a value of
and gradually change it, it stays
proper and orthochronous. But in addition its determinant stays 1 and
its time-dilatation entry stays greater or equal to 1. The reasons
are essentially the same as before. You cannot gradually change from
a value of 1 or above to a value of  1 or below if there is nothing
in between.
1 or below if there is nothing
in between.
One consequence of the defining relation (A.13) merits
mentioning. If you premultiply both sides of the relation by
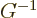 , you immediately see that
, you immediately see that
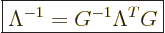 |
(A.14) |
This is the easy way to find inverses of Lorentz transforms. Also,
since 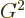

 ,
, 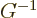

 . However, it
cannot hurt to leave the expression as written. There are other
applications in tensor algebra in which
. However, it
cannot hurt to leave the expression as written. There are other
applications in tensor algebra in which 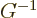 is not equal to
is not equal to
 .
.
As already illustrated above, what multiplications by  do is flip
over the sign of some entries. So to find an inverse of a Lorentz
transform, just flip over the right entries. To be precise, flip over
the entries in which one index is 0 and the other is not.
do is flip
over the sign of some entries. So to find an inverse of a Lorentz
transform, just flip over the right entries. To be precise, flip over
the entries in which one index is 0 and the other is not.
The above observations can be readily converted to tensor notation.
First an equivalent is needed to some definitions used in tensor
algebra but not normally in linear algebra. The “ lowered
covector” to a contravariant vector like position will be
defined as
In words, take a transpose and postmultiply with the metric  .
The result is a row vector while the original is a column vector.
.
The result is a row vector while the original is a column vector.
Note that the dot product can now be written as
Note also that lowered covectors are covariant vectors; they are row
vectors that transform with the inverse Lorentz transform. To check
that, simply plug in the Lorentz transformation of the original vector
and use the expression for the inverse Lorentz transform above.
Similarly, the raised contravector
to a covariant
vector like a gradient will be defined as
In words, take a transpose and premultiply by the inverse metric. The
raised contravector is a contravariant vector. Forming a raised
contravector of a lowered covector gives back the original vector.
And vice-versa. (Note that metrics are symmetric matrices in checking
that.)
In tensor notation, the lowered covector is written as
Note that the graphical effect of multiplying by the metric tensor is
to lower
the vector index.
Similarly, the raised contravector to a covector is
It shows that the inverse metric can be used to raise
indices. But do not forget the golden rule: raising or lowering an
index is much more than cosmetic: you produce a fundamentally
different vector.
(That is not true for so-called “Cartesian tensors” like purely spatial position vectors. For
these the metric  is the unit matrix. Then raising or lowering an
index has no real effect. By the way, the unit matrix is in tensor
notation
is the unit matrix. Then raising or lowering an
index has no real effect. By the way, the unit matrix is in tensor
notation 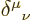 . That is called the Kronecker
delta. Its entries are 1 if the two indices are equal and 0
otherwise.)
. That is called the Kronecker
delta. Its entries are 1 if the two indices are equal and 0
otherwise.)
Using the above notations, the dot product becomes as stated in
chapter 1.2.5,
More interestingly, consider the inverse Lorentz transform. According
to the expression given above 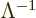

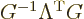 , so:
, so:
(A transpose of a matrix, in this case 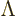 , swaps the
indices.) According the index raising/lowering conventions above, in
the right hand side the heights of the indices of
, swaps the
indices.) According the index raising/lowering conventions above, in
the right hand side the heights of the indices of 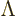 are
inverted. So you can define a new matrix with entries
are
inverted. So you can define a new matrix with entries
But note that the so-defined matrix is not the Lorentz
transform matrix:
It is a different matrix. In particular, the signs on some entries
are swapped.
(Needless to say, various supposedly authoritative sources list both
matrices as 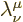 for that exquisite final bit of
confusion. It is apparently not easy to get subscripts and
superscripts straight if you use some horrible product like MS Word.
Of course, the simple answer would be to use a place holder in the
empty position that indicates whether or not the index has been raised
or lowered. For example:
for that exquisite final bit of
confusion. It is apparently not easy to get subscripts and
superscripts straight if you use some horrible product like MS Word.
Of course, the simple answer would be to use a place holder in the
empty position that indicates whether or not the index has been raised
or lowered. For example:
However, this is not possible because it would add clarity.)
Now consider another very confusing result. Start with
According to the raising conventions, that can be written
as
 |
(A.15) |
Does this not look exactly as if 

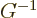 ? That may
be true in the case of Lorentz transforms and the associated Minkowski
metric. But for more general applications of tensor algebra it is
most definitely not true. Always remember the golden rule:
names of tensors are only meaningful if the indices are at the right
height. The right height for the indices of
? That may
be true in the case of Lorentz transforms and the associated Minkowski
metric. But for more general applications of tensor algebra it is
most definitely not true. Always remember the golden rule:
names of tensors are only meaningful if the indices are at the right
height. The right height for the indices of  is subscripts. So
is subscripts. So
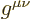 does not indicate an entry of
does not indicate an entry of  . Instead
it turns out to represent an entry of
. Instead
it turns out to represent an entry of 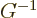 .
.
So physicists now have two options. They can write the entries of
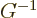 in the understandable form
in the understandable form
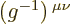 . Or they can use the
confusing, error-prone form
. Or they can use the
confusing, error-prone form 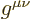 . So what do you
think they all do? If you guessed option (b), you are making real
progress in your study of modern physics.
. So what do you
think they all do? If you guessed option (b), you are making real
progress in your study of modern physics.
Often the best way to verify some arcane tensor expression is to
convert it to linear algebra. (Remember to check the heights of the
indices when doing so. If they are on the wrong height, restore the
omitted factor 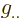 or
or 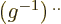 .) Some
additional results that are useful in this context are
.) Some
additional results that are useful in this context are
The first of these implies that the inverse of a Lorentz transform is
a Lorentz transform too. That is readily verified from the defining
relation (A.13) by premultiplying by 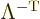 and postmultiplying by
and postmultiplying by 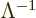 . The second expression is
simply the matrix inverse of the first. Both of these expressions
generalize to any symmetric metric
. The second expression is
simply the matrix inverse of the first. Both of these expressions
generalize to any symmetric metric  . The final expression
implies that the transpose of a Lorentz transform is a Lorentz
transform too. That is only true for Lorentz transforms and the
associated Minkowski metric. Or actually, it is also true for any
other metric in which
. The final expression
implies that the transpose of a Lorentz transform is a Lorentz
transform too. That is only true for Lorentz transforms and the
associated Minkowski metric. Or actually, it is also true for any
other metric in which 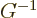

 , including Cartesian
tensors. For these metrics, the final expression above is the same as
the second expression.
, including Cartesian
tensors. For these metrics, the final expression above is the same as
the second expression.
![]() .
.![]() :
:![\begin{displaymath}
\kern-1pt{\buildrel\raisebox{-1.5pt}[0pt][0pt]
{\hbox{\hspa...
...& 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1
\end{array} \right)
\end{displaymath}](img3647.gif)
![]()
![]()
![]()
![]() .
.![]() ,
,![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]() .
.![]()
![]()
![]() .
.![]()
![]()
![]() .
.![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]() 1
1![]()
![]() 1
1![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]() 1
1![]() 1
1![]()
![]()
![]()
![]() 1
1![]() ,
,![]()
![]()
![]() .
.![]()
![]()
![]() .
.![]() .
.![]()
![]() .
.