| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
D.38 Time-dependent perturbation theory
The equations to be solved are
To simplify the use of perturbation theory, it is convenient to use a
trick that gets rid of half the terms in these equations. The trick
is to define new coefficients 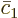 and
and 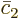 by
by
 |
(D.22) |
The new coefficients 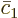 and
and 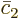 are physically just
as good as
are physically just
as good as 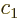 and
and  . For one, the probabilities are
given by the square magnitudes of the coefficients, and the square
magnitudes of
. For one, the probabilities are
given by the square magnitudes of the coefficients, and the square
magnitudes of 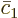 and
and 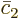 are exactly the same as
those of
are exactly the same as
those of 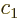 and
and  . That is because the exponentials have
magnitude one. Also, the initial conditions are unchanged, assuming
that you choose the integration constants so that the integrals are
initially zero.
. That is because the exponentials have
magnitude one. Also, the initial conditions are unchanged, assuming
that you choose the integration constants so that the integrals are
initially zero.
The evolution equations for 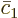 and
and 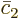 are
are
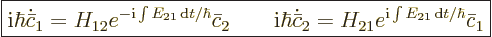 |
(D.23) |
with 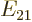

 .
Effectively, the two energy expectation values have been turned into
zero. However, the matrix element is now time-dependent, if it was
not already. To check the above evolution equations, just plug in the
definition of the coefficients.
.
Effectively, the two energy expectation values have been turned into
zero. However, the matrix element is now time-dependent, if it was
not already. To check the above evolution equations, just plug in the
definition of the coefficients.
It will from now on be assumed that the original Hamiltonian
coefficients are independent of time. That makes the difference in
expectation energies 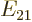 constant too.
constant too.
Now the formal way to perform time-dependent perturbation theory is to
assume that the matrix element 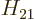 is small. Write
is small. Write 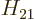 as
as
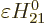 where
where  is a scale factor. Then
you can find the behavior of the solution in the limiting process
is a scale factor. Then
you can find the behavior of the solution in the limiting process
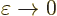 by expanding the solution in powers of
by expanding the solution in powers of
 . The definition of the scale factor
. The definition of the scale factor  is not important. You might identify it with a small physical
parameter in the matrix element. But in fact you can take
is not important. You might identify it with a small physical
parameter in the matrix element. But in fact you can take 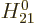 the same as
the same as 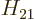 and
and  as an additional mathematical
parameter with no meaning for the physical problem. In that approach,
as an additional mathematical
parameter with no meaning for the physical problem. In that approach,
 disappears when you take it to be 1 in the final answer.
disappears when you take it to be 1 in the final answer.
But because the problem here is so trivial, there is really no need
for a formal time-dependent perturbation expansion. In particular, by
assumption the system stays close to state  , so the
coefficient
, so the
coefficient 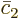 must remain small. Then the evolution
equations above show that
must remain small. Then the evolution
equations above show that 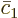 will hardly change. That allows
it to be treated as a constant in the evolution equation for
will hardly change. That allows
it to be treated as a constant in the evolution equation for
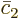 . That then allows
. That then allows 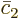 to be found by simple
integration. The integration constant follows from the condition that
to be found by simple
integration. The integration constant follows from the condition that
 is zero at the initial time. That then gives the result cited
in the text.
is zero at the initial time. That then gives the result cited
in the text.
It may be noted that for the analysis to be valid, 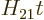

 must be small. That ensures that
must be small. That ensures that 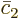 is correspondingly small
according to its evolution equation. And then the change in
is correspondingly small
according to its evolution equation. And then the change in
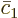 from its original value is small of order
from its original value is small of order
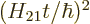 according to its evolution equation. So the
assumption that it is about constant in the equation for
according to its evolution equation. So the
assumption that it is about constant in the equation for 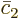 is verified. The error will be of order
is verified. The error will be of order 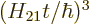 .
.
To be sure, this does not verify that this error in 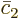 decays
to zero when
decays
to zero when 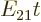

 tends to infinity. But it does, as can
be seen from the exact solution,
tends to infinity. But it does, as can
be seen from the exact solution,
By splitting it up into ranges 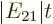

 no larger than
no larger than
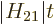

 and
and 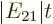

 no larger than 1, you can see
that the error is never larger than order
no larger than 1, you can see
that the error is never larger than order 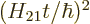 for
for
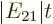

 no larger than 1. And it is of order
no larger than 1. And it is of order
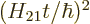

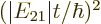 outside that range.
outside that range.
Finally, consider the case that the state cannot just transition to
one state  but to a large number
but to a large number 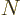 of them, each with its
own coefficient
of them, each with its
own coefficient 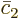 . In that case, the individual
contributions of all these states add up to change
. In that case, the individual
contributions of all these states add up to change 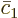 .
And
.
And 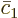 must definitely stay approximately constant for the
above analysis to be valid. Fortunately, if you plug the approximate
expressions for the
must definitely stay approximately constant for the
above analysis to be valid. Fortunately, if you plug the approximate
expressions for the 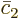 into the evolution equation for
into the evolution equation for
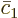 , you can see that
, you can see that 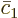 stays approximately
constant as long as the sum of all the transition probabilities does.
So as long as there is little probability of any transition at
time
stays approximately
constant as long as the sum of all the transition probabilities does.
So as long as there is little probability of any transition at
time  , time-dependent perturbation theory should be OK.
, time-dependent perturbation theory should be OK.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
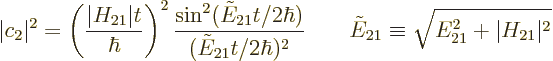
![]()
![]()
![]() .
.![]() .
.![]()
![]()
![]() ,
,![]()
![]() ,
,