| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
D.39 Selection rules
This note derives the selection rules for electric dipole transitions
between two hydrogen states  and
and  .
Some selection rules for forbidden transitions are also derived. The
derivations for forbidden transitions use some more advanced results
from later chapters. It may be noted that in any case, the
Hamiltonian assumes that the velocity of the electrons is small
compared to the speed of light.
.
Some selection rules for forbidden transitions are also derived. The
derivations for forbidden transitions use some more advanced results
from later chapters. It may be noted that in any case, the
Hamiltonian assumes that the velocity of the electrons is small
compared to the speed of light.
According to chapter 4.3, the hydrogen states take the form


 and
and


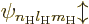 . Here 1
. Here 1 
 , 0
, 0 


 and
and 

 are integer
quantum numbers. The final
are integer
quantum numbers. The final 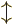 represents the electron spin state,
up or down.
represents the electron spin state,
up or down.
As noted in the text, allowed electric dipole transitions must respond
to at least one component of a constant ambient electric field. That
means that they must have a nonzero value for at least one electrical
dipole moment,
where 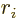 can be one of
can be one of 

 ,
, 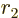

 , or
, or 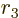

 for the three different components of
the electric field.
for the three different components of
the electric field.
The trick in identifying when these inner products are zero is based
on taking inner products with cleverly chosen commutators. Since the
hydrogen states are eigenfunctions of  , the following
commutator is useful
, the following
commutator is useful
For the 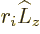 term in the right hand side, the operator
term in the right hand side, the operator  acts on
acts on  and produces a factor
and produces a factor 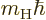 ,
while for the
,
while for the 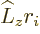 term,
term,  can be taken to the other side of
the inner product and then acts on
can be taken to the other side of
the inner product and then acts on  , producing a
factor
, producing a
factor 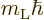 . So:
. So:
![\begin{displaymath}
\langle \psi_{\rm {L}}\vert [r_i,\L _z]\vert\psi_{\rm {H}}\...
...ar
\langle\psi_{\rm {L}}\vert r_i\vert\psi_{\rm {H}}\rangle %
\end{displaymath}](img6611.gif) |
(D.24) |
The final inner product is the dipole moment of interest. Therefore,
if a suitable expression for the commutator in the left hand side can
be found, it will fix the dipole moment.
In particular, according to chapter 4.5.4 ![$[z,\L _z]$](img6612.gif) is
zero. That means according to equation (D.24) above that the
dipole moment
is
zero. That means according to equation (D.24) above that the
dipole moment 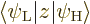 in the
right hand side will have to be zero too, unless
in the
right hand side will have to be zero too, unless 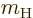

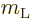 . So the first conclusion is that the
. So the first conclusion is that the  -component
of the electric field does not do anything unless
-component
of the electric field does not do anything unless 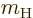

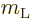 . One down, two to go.
. One down, two to go.
For the  and
and  components, from chapter 4.5.4
components, from chapter 4.5.4
Plugging that into (D.24) produces
From these equations it is seen that the  dipole moment is zero if
the
dipole moment is zero if
the  one is, and vice-versa. Further, plugging the
one is, and vice-versa. Further, plugging the  dipole
moment from the first equation into the second produces
dipole
moment from the first equation into the second produces
and if the  dipole moment is nonzero, that requires that
dipole moment is nonzero, that requires that
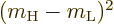 is one, so
is one, so 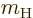

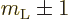 . It follows that dipole transitions can only
occur if
. It follows that dipole transitions can only
occur if 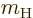

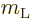 , through the
, through the  component of the electric field, or if
component of the electric field, or if 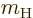

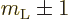 , through the
, through the  and
and  components.
components.
To derive selection rules involving the azimuthal quantum numbers
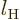 and
and 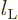 , the obvious approach would be to
try the commutator
, the obvious approach would be to
try the commutator ![$[r_i,\L ^2]$](img6619.gif) since
since 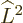 produces
produces
 . However, according to chapter
4.5.4, (4.68), this commutator will bring
in the
. However, according to chapter
4.5.4, (4.68), this commutator will bring
in the 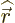

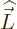 operator, which cannot be handled. The
commutator that works is the second of (4.73):
operator, which cannot be handled. The
commutator that works is the second of (4.73):
where by the definition of the commutator
Evaluating
![$\langle\psi_{\rm {L}}\vert[[r_i,\L ^2],\L ^2]\vert\psi_{\rm {H}}\rangle$](img6622.gif) according to each of the two equations above and equating the results
gives
according to each of the two equations above and equating the results
gives
For 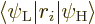 to be nonzero, the
numerical factors in the left and right hand sides must be equal,
to be nonzero, the
numerical factors in the left and right hand sides must be equal,
The right hand side is obviously zero for 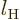

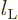 , so
, so  can be factored out of
it as
can be factored out of
it as
and the left hand side can be written in terms of these same factors
as
Equating the two results and simplifying gives
The second factor is only zero if 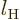

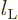
 0, but then
0, but then 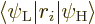 is
still zero because both states are spherically symmetric. It follows
that the first factor will have to be zero for dipole transitions to
be possible, and that means that
is
still zero because both states are spherically symmetric. It follows
that the first factor will have to be zero for dipole transitions to
be possible, and that means that 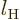

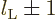 .
.
The spin is not affected by the perturbation Hamiltonian, so the
dipole moment inner products are still zero unless the spin magnetic
quantum numbers  are the same, both spin-up or both spin-down.
Indeed, if the electron spin is not affected by the electric field to
the approximations made, then obviously it cannot change. That
completes the selection rules as given in chapter 7.4.4
for electric dipole transitions.
are the same, both spin-up or both spin-down.
Indeed, if the electron spin is not affected by the electric field to
the approximations made, then obviously it cannot change. That
completes the selection rules as given in chapter 7.4.4
for electric dipole transitions.
Now consider the effect of the magnetic field on transitions. For
such transitions to be possible, the matrix element formed with the
magnetic field must be nonzero. Like the electric field, the magnetic
field can be approximated as spatially constant and quasi-steady. The
perturbation Hamiltonian of a constant magnetic field is according to
chapter 13.4
Note that now electron spin must be included in the discussion.
According to this perturbation Hamiltonian, the perturbation
coefficient 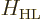 for the
for the  -component of the magnetic field
is proportional to
-component of the magnetic field
is proportional to
and that is zero because 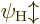 is an eigenfunction of
both operators and orthogonal to
is an eigenfunction of
both operators and orthogonal to  . So the
. So the
 -component of the magnetic field does not produce transitions to
different states.
-component of the magnetic field does not produce transitions to
different states.
However, the  -component (and similarly the
-component (and similarly the
 -component) produces a perturbation coefficient
proportional to
-component) produces a perturbation coefficient
proportional to
According to chapter 12.11, the effect of 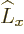 on a state
with magnetic quantum number
on a state
with magnetic quantum number 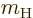 is to turn it into a linear
combination of two similar states with magnetic quantum numbers
is to turn it into a linear
combination of two similar states with magnetic quantum numbers
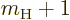 and
and 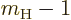 . Therefore, for the first
inner product above to be nonzero,
. Therefore, for the first
inner product above to be nonzero, 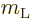 will have to be either
will have to be either
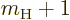 or
or 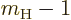 . Also the orbital azimuthal
momentum numbers
. Also the orbital azimuthal
momentum numbers  will need to be the same, and so will the spin
magnetic quantum numbers
will need to be the same, and so will the spin
magnetic quantum numbers  . And the principal quantum
numbers
. And the principal quantum
numbers  , for that matter; otherwise the radial parts of the
wave fuctions are orthogonal.
, for that matter; otherwise the radial parts of the
wave fuctions are orthogonal.
The magnetic field simply wants to rotate the orbital angular momentum
vector in the hydrogen atom. That does not change the energy, in the
absence of an average ambient magnetic field. For the second inner
product, the spin magnetic quantum numbers have to be different by one
unit, while the orbital magnetic quantum numbers must now be equal.
So, all together
and either the orbital or the spin magnetic quantum numbers must be
unequal. That are the selection rules as given in chapter
7.4.4 for magnetic dipole transitions. Since the
energy does not change in these transitions, Fermi’s golden
rule would have the decay rate zero. Fermi’s analysis
is not exact, but such transitions should be very rare.
The logical way to proceed to electric quadrupole transitions would be
to expand the electric field in a Taylor series in terms of  :
:
The first term is the constant electric field of the electric dipole
approximation, and the second would then give the electric quadrupole
approximation. However, an electric field in which 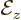 is a
multiple of
is a
multiple of  is not conservative, so the electrostatic potential
does no longer exist.
is not conservative, so the electrostatic potential
does no longer exist.
It is necessary to retreat to the so-called vector potential
 . It is then simplest to chose this potential to get rid
of the electrostatic potential altogether. In that case the typical
electromagnetic wave is described by the vector potential
. It is then simplest to chose this potential to get rid
of the electrostatic potential altogether. In that case the typical
electromagnetic wave is described by the vector potential
In terms of the vector potential, the perturbation Hamiltonian is,
chapter 13.1 and 13.4, and assuming a
weak field,
Ignoring the spatial variation of  , this expression
produces an Hamiltonian coefficient
, this expression
produces an Hamiltonian coefficient
That should be same as for the electric dipole approximation, since
the field is now completely described by  , but it is not
quite. The earlier derivation assumed that the electric field is
quasi-steady. However,
, but it is not
quite. The earlier derivation assumed that the electric field is
quasi-steady. However,  is equal to the commutator
is equal to the commutator
![${{\rm i}}m_{\rm e}[H_0,z]$](img6643.gif)

 where
where  is the unperturbed hydrogen atom
Hamiltonian. If that is plugged in and expanded, it is found that the
expressions are equivalent, provided that the perturbation frequency
is close to the frequency of the photon released in the transition,
and that that frequency is sufficiently rapid that the phase shift
from sine to cosine can be ignored. Those are in fact the normal
conditions.
is the unperturbed hydrogen atom
Hamiltonian. If that is plugged in and expanded, it is found that the
expressions are equivalent, provided that the perturbation frequency
is close to the frequency of the photon released in the transition,
and that that frequency is sufficiently rapid that the phase shift
from sine to cosine can be ignored. Those are in fact the normal
conditions.
Now consider the second term in the Taylor series of  with
respect to
with
respect to  . It produces a perturbation Hamiltonian
. It produces a perturbation Hamiltonian
The factor 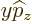 can be trivially rewritten to give
can be trivially rewritten to give
The first term has already been accounted for in the magnetic dipole
transitions discussed above, because the factor within parentheses is
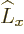 . The second term is the electric quadrupole Hamiltonian
for the considered wave.
. The second term is the electric quadrupole Hamiltonian
for the considered wave.
As second terms in the Taylor series, both Hamiltonians will be much
smaller than the electric dipole one. The factor that they are
smaller can be estimated from comparing the first and second term in
the Taylor series. Note that 

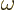 is proportional to the wave
length
is proportional to the wave
length 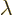 of the electromagnetic wave. Also, the additional
position coordinate in the operator scales with the atom size, call it
of the electromagnetic wave. Also, the additional
position coordinate in the operator scales with the atom size, call it
 . So the factor that the magnetic dipole and electric
quadrupole matrix elements are smaller than the electric dipole one is
. So the factor that the magnetic dipole and electric
quadrupole matrix elements are smaller than the electric dipole one is


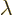 . Since transition probabilities are proportional
to the square of the corresponding matrix element, it follows that,
all else being the same, magnetic dipole and electric quadrupole
transitions are slower than electric dipole ones by a factor
. Since transition probabilities are proportional
to the square of the corresponding matrix element, it follows that,
all else being the same, magnetic dipole and electric quadrupole
transitions are slower than electric dipole ones by a factor
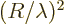 . (But note the earlier remark on the problem
for the hydrogen atom that the energy does not change in magnetic
dipole transitions.)
. (But note the earlier remark on the problem
for the hydrogen atom that the energy does not change in magnetic
dipole transitions.)
The selection rules for the electric quadrupole Hamiltonian can be
narrowed down with a bit of simple reasoning. First, since the
hydrogen eigenfunctions are complete, applying any operator on an
eigenfunction will always produce a linear combination of
eigenfunctions. Now reconsider the derivation of the electric dipole
selection rules above from that point of view. It is then seen that
 only produces eigenfunctions with the same values of
only produces eigenfunctions with the same values of  and the
values of
and the
values of  exactly one unit different. The operators
exactly one unit different. The operators  and
and  change both
change both  and
and  by exactly one unit. And the components of
linear momentum do the same as the corresponding components of
position, since
by exactly one unit. And the components of
linear momentum do the same as the corresponding components of
position, since 

![${{\rm i}}m_{\rm e}[H_0,r_i]$](img6648.gif)

 and
and  does not change the eigenfunctions, just their coefficients.
Therefore
does not change the eigenfunctions, just their coefficients.
Therefore  produces only eigenfunctions with azimuthal
quantum number
produces only eigenfunctions with azimuthal
quantum number  either equal to
either equal to  or to
or to
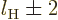 , depending on whether the two unit changes
reinforce or cancel each other. Furthermore, it produces only
eigenfunctions with
, depending on whether the two unit changes
reinforce or cancel each other. Furthermore, it produces only
eigenfunctions with  equal to
equal to 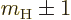 . However,
. However,
 , corresponding to a wave along another axis, will
produce values of
, corresponding to a wave along another axis, will
produce values of  equal to
equal to 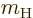 or to
or to
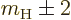 . Therefore the selection rules become:
. Therefore the selection rules become:
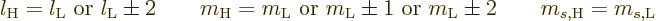
That are the selection rules as given in chapter 7.4.4
for electric quadrupole transitions. These arguments apply equally
well to the magnetic dipole transition, but there the possibilities
are narrowed down much further because the angular momentum operators
only produce a couple of eigenfunctions. It may be noted that in
addition, electric quadrupole transitions from 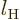
 0 to
0 to
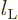
 0 are not possible because of spherical symmetry.
0 are not possible because of spherical symmetry.
![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]() .
.![]() -
-![]()
![]()
![]() .
.![]()
![]()
![]()
![]() ,
,![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
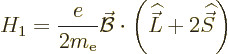
![]()
![]() -
-![]() -
-![]() -
-![]() :
:![]() .
.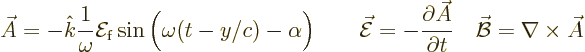
![]()
![]() .
.![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]() .
.![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]() .
.![]() ,
,![]()
![]()
![]() .
.