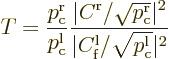| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
A.29 WKB solution near the turning points
Both the classical and tunneling WKB approximations of addendum
{A.28} fail near so-called turning points
where the classical kinetic energy  becomes zero. This note
explains how the problem can be fixed.
becomes zero. This note
explains how the problem can be fixed.
Figure A.17:
The Airy Ai and Bi
functions that solve the Hamiltonian eigenvalue problem for a
linearly varying potential energy. Bi very quickly becomes too
large to plot for positive values of its argument.
![\begin{figure}\centering
\setlength{\unitlength}{1pt}
\begin{picture}(400,13...
...makebox(0,0)[t]{1}}
\put(100,53){\makebox(0,0){Bi}}
\end{picture}
\end{figure}](img5066.gif) |
The trick is to use a different approximation near turning points. In
a small vicinity of a turning point, it can normally be assumed that
the  -derivative
-derivative  of the potential is about constant, so that
the potential varies linearly with position. Under that condition,
the exact solution of the Hamiltonian eigenvalue problem is known to
be a combination of two special functions Ai and Bi that are called
the
of the potential is about constant, so that
the potential varies linearly with position. Under that condition,
the exact solution of the Hamiltonian eigenvalue problem is known to
be a combination of two special functions Ai and Bi that are called
the Airy
functions. These functions are shown in
figure A.17. The general solution near a turning point
is:
Note that 

 is the
is the  -position measured from the point
where
-position measured from the point
where 

 , so that
, so that 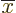 is a local,
stretched
is a local,
stretched  -coordinate.
-coordinate.
The second step is to relate this solution to the normal WKB
approximations away from the turning point. Now from a macroscopic
point of view, the WKB approximation follows from the assumption that
Planck’s constant  is very small. That implies that the
validity of the Airy functions normally extends to region where
is very small. That implies that the
validity of the Airy functions normally extends to region where
 is relatively large. For example, if you focus
attention on a point where
is relatively large. For example, if you focus
attention on a point where  is a finite multiple of
is a finite multiple of
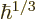 ,
,  is small, so the value of
is small, so the value of  will deviate
little from its value at the turning point: the assumption of linearly
varying potential remains valid. Still, if
will deviate
little from its value at the turning point: the assumption of linearly
varying potential remains valid. Still, if  is a finite multiple
of
is a finite multiple
of 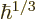 ,
,  will be proportional to
1/
will be proportional to
1/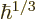 , and that is large. Such regions of large, but
not too large,
, and that is large. Such regions of large, but
not too large,  are called “matching regions,” because in them both the Airy
function solution and the WKB solution are valid. It is where the two
meet and must agree.
are called “matching regions,” because in them both the Airy
function solution and the WKB solution are valid. It is where the two
meet and must agree.
Figure A.18:
Connection formulae for a turning point from normal
motion to tunneling.
![\begin{figure}\centering
\setlength{\unitlength}{1pt}
\begin{picture}(405,22...
...\gamma}\right]$}}
\put(18,173){\makebox(0,0)[b]{t}}
\end{picture}
\end{figure}](img5071.gif) |
Figure A.19:
Connection formulae for a turning point from tunneling to
normal motion.
![\begin{figure}\centering
\setlength{\unitlength}{1pt}
\begin{picture}(405,22...
...array}\right.$}}
\put(-23,173){\makebox(0,0)[b]{t}}
\end{picture}
\end{figure}](img5072.gif) |
It is graphically depicted in figures A.18 and
A.19. Away from the turning points, the classical or
tunneling WKB approximations apply, depending on whether the total
energy is more than the potential energy or less. In the vicinity of
the turning points, the solution is a combination of the Airy
functions. If you look up in a mathematical handbook like
[1] how the Airy functions can be approximated
for large positive respectively negative 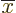 , you
find the expressions listed in the bottom lines of the figures.
(After you rewrite what you find in table books in terms of useful
quantities, that is!)
, you
find the expressions listed in the bottom lines of the figures.
(After you rewrite what you find in table books in terms of useful
quantities, that is!)
The expressions in the bottom lines must agree with what the
classical, respectively tunneling WKB approximation say about the
matching regions. At one side of the turning point, that relates the
coefficients 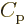 and
and 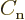 of the tunneling
approximation to the coefficients of
of the tunneling
approximation to the coefficients of 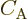 and
and 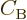 of
the Airy functions. At the other side, it relates the coefficients
of
the Airy functions. At the other side, it relates the coefficients
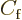 and
and 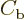 (or
(or 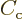 and
and 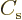 ) of
the classical WKB approximation to
) of
the classical WKB approximation to 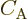 and
and
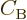 . The net effect of it all is to relate,
. The net effect of it all is to relate,
connect,
the coefficients of the classical WKB
approximation to those of the tunneling one. That is why the formulae
in figures A.18 and A.19 are called
the “connection formulae.”
You may have noted the appearance of an additional constant  in
figures A.18 and A.19. This nasty
constant is defined as
in
figures A.18 and A.19. This nasty
constant is defined as
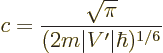 |
(A.215) |
and shows up uninvited when you approximate the Airy function solution
for large  . By cleverly absorbing it in a
redefinition of the constants
. By cleverly absorbing it in a
redefinition of the constants 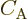 and
and 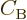 ,
figures A.18 and A.19 achieve that you
do not have to worry about it unless you specifically need the actual
solution at the turning points.
,
figures A.18 and A.19 achieve that you
do not have to worry about it unless you specifically need the actual
solution at the turning points.
As an example of how the connection formulae are used, consider a
right turning point for the harmonic oscillator or similar. Near such
a turning point, the connection formulae of figure
A.18 apply. In the tunneling region towards the
right, the term 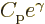 better be zero, because it
blows up at large
better be zero, because it
blows up at large  , and that would put the particle at
infinity for sure. So the constant
, and that would put the particle at
infinity for sure. So the constant 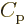 will have to be zero.
Now the matching at the right side equates
will have to be zero.
Now the matching at the right side equates 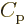 to
to
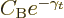 so
so 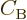 will have to be zero. That
means that the solution in the vicinity of the turning point will have
to be a pure Ai function. Then the matching towards the left shows
that the solution in the classical WKB region must take the form of a
sine that, when extrapolated to the turning point
will have to be zero. That
means that the solution in the vicinity of the turning point will have
to be a pure Ai function. Then the matching towards the left shows
that the solution in the classical WKB region must take the form of a
sine that, when extrapolated to the turning point 

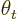 , stops short of reaching zero by an angular amount
, stops short of reaching zero by an angular amount
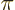
 4. Hence the assertion in addendum {A.28} that the
angular range of the classical WKB solution should be shortened by
4. Hence the assertion in addendum {A.28} that the
angular range of the classical WKB solution should be shortened by
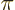
 4 for each end at which the particle is trapped by a gradually
increasing potential instead of an impenetrable wall.
4 for each end at which the particle is trapped by a gradually
increasing potential instead of an impenetrable wall.
Figure A.20:
WKB approximation of tunneling.
![\begin{figure}\centering
\setlength{\unitlength}{1pt}
\begin{picture}(405,65...
...kebox(0,0)[b]{V}}
\put(-65,35){\makebox(0,0)[b]{E}}
\end{picture}
\end{figure}](img5081.gif) |
As another example, consider tunneling as discussed in chapter
7.12 and 7.13. Figure A.20
shows a sketch. The WKB approximation may be used if the barrier
through which the particle tunnels is high and wide. In the far right
region, the energy eigenfunction only involves a term
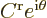 with a forward wave speed. To simplify
the analysis, the constant
with a forward wave speed. To simplify
the analysis, the constant 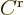 can be taken to be one,
because it does not make a difference how the wave function is
normalized. Also, the integration constant in
can be taken to be one,
because it does not make a difference how the wave function is
normalized. Also, the integration constant in  can be chosen
such that
can be chosen
such that 

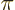
 4 at turning point 2; then the
connection formulae of figure A.19 along with the
Euler formula (2.5) show that the coefficients of the Airy
functions at turning point 2 are
4 at turning point 2; then the
connection formulae of figure A.19 along with the
Euler formula (2.5) show that the coefficients of the Airy
functions at turning point 2 are 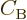
 1 and
1 and 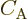

 . Next, the integration constant in
. Next, the integration constant in  can be
taken such that
can be
taken such that 
 0 at turning point 2; then the
connection formulae of figure A.19 imply that
0 at turning point 2; then the
connection formulae of figure A.19 imply that


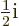 and
and 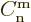
 1.
1.
Next consider the connection formulae for turning point 1 in figure
A.18. Note that  can be written as
can be written as
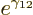 , where
, where 

 , because the integration constant in
, because the integration constant in
 was chosen such that
was chosen such that 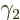
 0. The advantage of
using
0. The advantage of
using 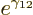 instead of
instead of  is that it is
independent of the choice of integration constant. Furthermore, under
the typical conditions that the WKB approximation applies, for a high
and wide barrier,
is that it is
independent of the choice of integration constant. Furthermore, under
the typical conditions that the WKB approximation applies, for a high
and wide barrier, 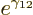 will be a very large number. It
is then seen from figure A.18 that near turning point
1,
will be a very large number. It
is then seen from figure A.18 that near turning point
1, 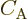

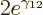 which is large while
which is large while
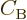 is small and will be ignored. And that then implies,
using the Euler formula to convert Ai’s sine into exponentials,
that
is small and will be ignored. And that then implies,
using the Euler formula to convert Ai’s sine into exponentials,
that 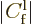

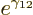 . As
discussed in chapter 7.13, the transmission coefficient
is given by
. As
discussed in chapter 7.13, the transmission coefficient
is given by
and plugging in 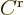
 1 and
1 and 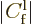

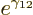 , the transmission coefficient is found to be
, the transmission coefficient is found to be
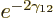 .
.
![]()
![\begin{figure}\centering
\setlength{\unitlength}{1pt}
\begin{picture}(400,13...
...makebox(0,0)[t]{1}}
\put(100,53){\makebox(0,0){Bi}}
\end{picture}
\end{figure}](img5066.gif)
![]() -
-![]()
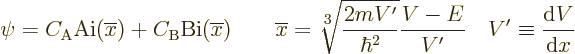
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]() ,
,![]()
![]() ,
,![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() )
)![]()
![]() .
.![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.