A.26 WKB Theory of Nearly Classical Motion

WKB theory provides simple approximate solutions for the energy eigenfunctions when the conditions are almost classical, like for the wave packets of chapter 7.11. The approximation is named after Wentzel, Kramers, and Brillouin, who refined the ideas of Liouville and Green. The bandit scientist Jeffreys tried to rob WKB of their glory by doing the same thing two years earlier, and is justly denied all credit.

Figure A.16: Harmonic oscillator potential energy $V$, eigenfunction $h_{50}$, and its energy $E_{50}$.

The WKB approximation is based on the rapid spatial variation of energy eigenfunctions with almost macroscopic energies. As an example, figure A.16 shows the harmonic oscillator energy eigenfunction $h_{50}$. Its energy $E_{50}$ is hundred times the ground state energy. That makes the kinetic energy $E-V$ quite large over most of the range, and that in turn makes the linear momentum large. In fact, the classical Newtonian linear momentum $p_{\rm {c}}=mv$ is given by

$$\fbox{$\displaystyle p_{\rm{c}} \equiv \sqrt{2m(E-V)} $} %$$ (A.206)

In quantum mechanics, the large momentum implies rapid oscillation of the wave function: quantum mechanics associates the linear momentum with the operator $\hbar{\rm d}/{\rm i}{\rm d}{x}$ that denotes spatial variation.

The WKB approximation is most appealing in terms of the classical momentum $p_{\rm {c}}$ as defined above. To find its form, in the Hamiltonian eigenvalue problem

$$-\frac{\hbar^2}{2m} \frac{{\rm d}^2\psi}{{\rm d}x^2} + V\psi = E\psi$$

take the $V\psi$ term to the other side and then rewrite $E-V$ in terms of the classical linear momentum. That produces

$$\frac{{\rm d}^2\psi}{{\rm d}x^2} = - \frac{p_{\rm {c}}^2}{\hbar^2}\psi %$$ (A.207)

Now under almost classical conditions, a single period of oscillation of the wave function is so short that normally $p_{\rm {c}}$ is almost constant over it. Then by approximation the solution of the eigenvalue problem over a single period is simply an arbitrary combination of two exponentials,

$$\psi \sim c_{\rm {f}} e^{{\rm i}p_{\rm {c}} x/\hbar} + c_{\rm {b}} e^{-{\rm i}p_{\rm {c}} x/\hbar}$$

where the constants $c_{\rm {f}}$ and $c_{\rm {b}}$ are arbitrary. (The subscripts denote whether the wave speed of the corresponding term is forward or backward.)

It turns out that to make the above expression work over more than one period, it is necessary to replace $p_{\rm {c}}x$ by the antiderivative $\int{p}_{\rm {c}}{\,\rm d}{x}$. Furthermore, the “constants” $c_{\rm {f}}$ and $c_{\rm {b}}$ must be allowed to vary from period to period proportional to $1/\sqrt{p_{\rm {c}}}$.

In short, the WKB approximation of the wave function is, {D.47}:

$$\fbox{$\displaystyle \mbox{classical WKB:} \qquad \psi... ...eta \equiv \frac{1}{\hbar} \int p_{\rm{c}} {\,\rm d}x $} %$$ (A.208)

where $C_{\rm {f}}$ and $C_{\rm {b}}$ are now true constants.

If you ever glanced at notes such as {D.12}, {D.14}, and {D.15}, in which the eigenfunctions for the harmonic oscillator and hydrogen atom were found, you recognize what a big simplification the WKB approximation is. Just do the integral for $\theta$ and that is it. No elaborate transformations and power series to grind down. And the WKB approximation can often be used where no exact solutions exist at all.

In many applications, it is more convenient to write the WKB approximation in terms of a sine and a cosine. That can be done by taking the exponentials apart using the Euler formula (2.5). It produces

$$\fbox{$\displaystyle \mbox{rephrased WKB:} \qquad \psi... ...eta \equiv \frac{1}{\hbar} \int p_{\rm{c}} {\,\rm d}x $} %$$ (A.209)

The constants $C_{\rm {c}}$ and $C_{\rm {s}}$ are related to the original constants $C_{\rm {f}}$ and $C_{\rm {b}}$ as

$$\fbox{$\displaystyle C_{\rm{c}} = C_{\rm{f}} + C_{\rm{b}... ...xtstyle\frac{1}{2}} (C_{\rm{c}} + {\rm i}C_{\rm{s}}) $} %$$ (A.210)

which allows you to convert back and forward between the two formulations as needed. Do note that either way, the constants depend on what you chose for the integration constant in the $\theta$ integral.

As an application, consider a particle stuck between two impenetrable walls at positions $x_1$ and $x_2$. An example would be the particle in a pipe that was studied way back in chapter 3.5. The wave function $\psi$ must become zero at both $x_1$ and $x_2$, since there is zero possibility of finding the particle outside the impenetrable walls. It is now smart to chose the integration constant in $\theta$ so that $\theta_1=0$. In that case, $C_{\rm {c}}$ must be zero for $\psi$ to be zero at $x_1$, (A.209). The wave function must be just the sine term. Next, for $\psi$ also to be zero at $x_2$, $\theta_2$ must be a whole multiple $n$ of $\pi$, because that are the only places where sines are zero. So $\theta_2-\theta_1=n\pi$, which means that

$$\fbox{$\displaystyle \mbox{particle between impenetrable... ...rm{c}}({\underline x}) {\,\rm d}{\underline x}= n \pi $} %$$ (A.211)

Recall that $p_{\rm {c}}$ was $\sqrt{2m(E-V)}$, so this is just an equation for the energy eigenvalues. It is an equation involving just an integral; it does not even require you to find the corresponding eigenfunctions!

It does get a bit more tricky for a case like the harmonic oscillator where the particle is not caught between impenetrable walls, but merely prevented to escape by a gradually increasing potential. Classically, such a particle would still be rigorously constrained between the so called “turning points” where the potential energy $V$ becomes equal to the total energy $E$, like the points 1 and 2 in figure A.16. But as the figure shows, in quantum mechanics the wave function does not become zero at the turning points; there is some chance for the particle to be found somewhat beyond the turning points.

A further complication arises since the WKB approximation becomes inaccurate in the immediate vicinity of the turning points. The problem is the requirement that the classical momentum can be approximated as a nonzero constant on a small scale. At the turning points the momentum becomes zero and that approximation fails.

However, it is possible to solve the Hamiltonian eigenvalue problem near the turning points assuming that the potential energy is not constant, but varies approximately linearly with position, {A.27}. Doing so and fixing up the WKB solution away from the turning points produces a simple result. The classical WKB approximation remains a sine, but at the turning points, $\sin\theta$ stays an angular amount $\pi/4$ short of becoming zero. (Or to be precise, it just seems to stay $\pi/4$ short, because the classical WKB approximation is no longer valid at the turning points.) Assuming that there are turning points with gradually increasing potential at both ends of the range, like for the harmonic oscillator, the total angular range will be short by an amount $\pi/2$.

Therefore, the expression for the energy eigenvalues becomes:

$$\fbox{$\displaystyle \mbox{particle trapped between turn... ... d}{\underline x} = (n-{\textstyle\frac{1}{2}}) \pi $} %$$ (A.212)

The WKB approximation works fine in regions where the total energy $E$ is less than the potential energy $V$. The classical momentum $p_{\rm {c}}=\sqrt{2m(E-V)}$ is imaginary in such regions, reflecting the fact that classically the particle does not have enough energy to enter them. But, as the nonzero wave function beyond the turning points in figure A.16 shows, quantum mechanics does allow some possibility for the particle to be found in regions where $E$ is less than $V$. It is loosely said that the particle can “tunnel” through, after a popular way for criminals to escape from jail. To use the WKB approximation in these regions, just rewrite it in terms of the magnitude $\vert p_{\rm {c}}\vert=\sqrt{2m(V-E)}$ of the classical momentum:

$$\fbox{$\displaystyle \mbox{tunneling WKB:}\qquad \psi ... ...\frac{1}{\hbar} \int \vert p_{\rm{c}}\vert {\,\rm d}x $} %$$ (A.213)

Note that $\gamma$ is the equivalent of the angle $\theta$ in the classical approximation.

Key Points

The WKB approximation applies to situations of almost macroscopic energy.

The WKB solution is described in terms of the classical momentum $p_{\rm {c}}\equiv\sqrt{2m(E-V)}$ and in particular its antiderivative $\theta=\int{p}_{\rm {c}}{\,\rm d}{x}/\hbar$.

The wave function can be written as (A.208) or (A.209), whatever is more convenient.

For a particle stuck between impenetrable walls, the energy eigenvalues can be found from (A.211).

For a particle stuck between a gradually increasing potential at both sides, the energy eigenvalues can be found from (A.212).

The “tunneling” wave function in regions that classically the particle is forbidden to enter can be approximated as (A.213). It is in terms of the antiderivative $\gamma=\int\vert p_{\rm {c}}\vert{\,\rm d}{x}/\hbar$.

A.26 Review Questions

1

Use the equation

$$\frac{1}{\hbar} \int_{{\underline x}=x_1}^{x_2} p_{\rm {c}}({\underline x}) {\,\rm d}{\underline x}= n \pi$$

to find the WKB approximation for the energy levels of a particle stuck in a pipe of chapter 3.5.5. The potential $V$ is zero inside the pipe, given by $0\le x\le\ell_x$

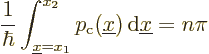
In this case, the WKB approximation produces the exact result, since the classical momentum really is constant. If there was a force field in the pipe, the solution would only be approximate.
Solution wkb-a

2

Use the equation

$$\frac{1}{\hbar} \int_{{\underline x}=x_1}^{x_2} p_{\rm {c}}(... ...e x}) {\,\rm d}{\underline x}= (n-{\textstyle\frac{1}{2}}) \pi$$

to find the WKB approximation for the energy levels of the harmonic oscillator. The potential energy is ${\textstyle\frac{1}{2}}m\omega{x}^2$ where the constant $\omega$ is the classical natural frequency. So the total energy, expressed in terms of the turning points $x_2=-x_1$ at which $E=V$, is $E={\textstyle\frac{1}{2}}m\omega{x_2}^2$.

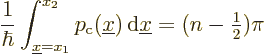
In this case too, the WKB approximation produces the exact energy eigenvalues. That, however, is just a coincidence; the classical WKB wave functions are certainly not exact; they become infinite at the turning points. As the example $h_{50}$ above shows, the true wave functions most definitely do not.
Solution wkb-b