| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
D.33 Quantum field derivations
This derivation will find the properties of a system described
by a Hamiltonian of the form:
Here 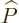 and
and  are Hermitian operators
with commutator
and
are Hermitian operators
with commutator
and 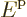 and
and 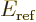 are constants with units of energy.
are constants with units of energy.
First note that the commutator (2) directly implies the uncertainty
relationship, chapter 4.5.2 (4.46):
Also note that the evolution equations for the expectation values of
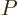 and
and  follow directly from chapter 7.2
(7.4). The commutator appearing in it is readily worked
out using the commutator (2) and the rules of chapter
4.5.4. Since energy eigenstates are stationary, according
to the evolution equations in such states the expectation values of
follow directly from chapter 7.2
(7.4). The commutator appearing in it is readily worked
out using the commutator (2) and the rules of chapter
4.5.4. Since energy eigenstates are stationary, according
to the evolution equations in such states the expectation values of
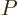 and
and  will have to be zero.
will have to be zero.
The equality of the 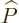 and
and  terms in the
Hamiltonian is a simple matter of symmetry. Nothing changes if you
swap
terms in the
Hamiltonian is a simple matter of symmetry. Nothing changes if you
swap 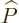 and
and  , adding a minus sign for
one. Then unavoidably the two terms in the Hamiltonian must be equal;
it is shown below that the eigenfunctions are unique.
, adding a minus sign for
one. Then unavoidably the two terms in the Hamiltonian must be equal;
it is shown below that the eigenfunctions are unique.
The commutator (2) also implies that 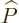 ,
,
 , and all their combinations, do not commute with
the Hamiltonian. So they are not conserved quantities of the system.
However, there are two combinations,
, and all their combinations, do not commute with
the Hamiltonian. So they are not conserved quantities of the system.
However, there are two combinations,
whose commutator with the Hamiltonian gives back a multiple of the
same thing:
In other words, 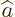 and
and 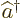 are commutator eigenoperators of the
Hamiltonian. The above relations are readily checked using the given
commutator (2) and the rules of chapter 4.5.4.
are commutator eigenoperators of the
Hamiltonian. The above relations are readily checked using the given
commutator (2) and the rules of chapter 4.5.4.
To see why that is important, multiply both sides of the eigenvalue
problems above with a system energy eigenfunction of energy  :
:
After writing out the definitions of the commutators, recognizing
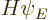 as
as 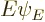 , and rearranging, that gives
, and rearranging, that gives
These results can be compared to the definition of an energy
eigenfunction. Then it is seen that  is an energy
eigenfunction with one unit
is an energy
eigenfunction with one unit 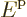 less energy than
less energy than 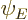 .
And
.
And 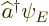 is an energy eigenfunction with one unit
is an energy eigenfunction with one unit 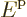 more
energy than
more
energy than 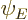 . So apparently
. So apparently 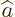 and
and 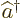 act as
annihilation and creation operators of quanta of energy
act as
annihilation and creation operators of quanta of energy 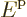 .
They act as shown to the left in figure A.6.
.
They act as shown to the left in figure A.6.
There are however two important caveats for these statements. If
 or
or 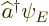 is zero, it is not an energy eigenfunction.
Eigenfunctions must be nonzero. Also, even if the states
is zero, it is not an energy eigenfunction.
Eigenfunctions must be nonzero. Also, even if the states  or
or 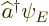 are not zero, they will not normally be normalized
states.
are not zero, they will not normally be normalized
states.
To get a better understanding of these issues, it is helpful to first
find the Hamiltonian in terms of 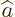 and
and 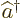 . There are two
equivalent forms,
. There are two
equivalent forms,
These expressions can be verified by plugging in the definitions (4)
of 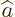 and
and 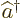 and using the commutator (2). (Note that
subtracting the two expressions gives the commutator of
and using the commutator (2). (Note that
subtracting the two expressions gives the commutator of 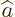 and
and
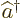 to be 1.)
to be 1.)
Now look at the first Hamiltonian first. If 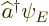 would be zero
for some state
would be zero
for some state 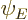 , then that state would have energy
, then that state would have energy
 . But that is not possible. If you
look at the original Hamiltonian (1), the energy must at least be
. But that is not possible. If you
look at the original Hamiltonian (1), the energy must at least be
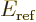 ; square Hermitian operators are nonnegative.
; square Hermitian operators are nonnegative.
(To be more precise, if you square a Hermitian operator, you square
the eigenvalues, making them nonnegative. It is said that the square
operator is positive definite,
or, if there are zero
eigenvalues, positive semi-definite. And such an operator produces
nonnegative expectation values. And the expectation values of the
operators in the Hamiltonian do add up to the total energy; just take
an inner product of the Hamiltonian eigenvalue problem with the wave
function. See chapter 4.4 for more information on
expectation values.)
It follows that 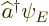 is never zero. This operator can be
applied indefinitely to find states of higher and higher energy. So
there is no maximum energy.
is never zero. This operator can be
applied indefinitely to find states of higher and higher energy. So
there is no maximum energy.
But there is a possibility that  is zero. As the second
form of the Hamiltonian in (5) shows, that requires that the energy
of state
is zero. As the second
form of the Hamiltonian in (5) shows, that requires that the energy
of state 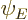 equals
equals
Now if you start from any energy state 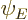 and apply
and apply 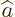 sufficiently many times, you must eventually end up at this energy
level. If not, you could go on lowering the energy forever. That
would be inconsistent with the fact that the energy cannot be lower
than
sufficiently many times, you must eventually end up at this energy
level. If not, you could go on lowering the energy forever. That
would be inconsistent with the fact that the energy cannot be lower
than 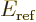 . It follows that the above energy is the
lowest energy that a state can have. So it is the ground state
energy.
. It follows that the above energy is the
lowest energy that a state can have. So it is the ground state
energy.
And any other energy must be a whole multiple of 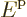 higher than the
ground state energy. Otherwise you could not end up at the ground
state energy by applying
higher than the
ground state energy. Otherwise you could not end up at the ground
state energy by applying 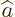 . Therefore, the energy
eigenstates can be denoted more meaningfully by
. Therefore, the energy
eigenstates can be denoted more meaningfully by 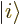 rather than
rather than
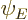 . Here
. Here  is the number of quanta
is the number of quanta 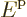 that the
energy is above the ground state level.
that the
energy is above the ground state level.
Now assume that the ground state is unique. In that case, there is
one unique energy eigenfunction at each energy level. That is a
consequence of the fact that if you go down a unit in energy with 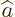 and then up a unit again with
and then up a unit again with 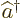 , (or vice versa), you must
end up not just at the same energy, but at the same state. Otherwise
the state would not be an eigenfunction of the Hamiltonian in one of
the forms given in (5). Repeated application shows that if you go
down any number of steps, and then up the same number of steps, you
end up at the same state. Since every state must end up at the unique
ground state, every state must be the result of applying
, (or vice versa), you must
end up not just at the same energy, but at the same state. Otherwise
the state would not be an eigenfunction of the Hamiltonian in one of
the forms given in (5). Repeated application shows that if you go
down any number of steps, and then up the same number of steps, you
end up at the same state. Since every state must end up at the unique
ground state, every state must be the result of applying 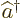 to the
ground state sufficiently many times. There is just one such state
for each energy level.
to the
ground state sufficiently many times. There is just one such state
for each energy level.
If there are two independent ground states, applying 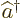 on each
gives two separate sets of energy eigenstates. And similar if there
are still more ground states. Additional symbols will need to be
added to the kets to keep the different families apart.
on each
gives two separate sets of energy eigenstates. And similar if there
are still more ground states. Additional symbols will need to be
added to the kets to keep the different families apart.
It was already mentioned that the states produced by the operators
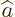 and
and 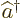 are usually not normalized. For example, the state
are usually not normalized. For example, the state
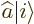 will have a square magnitude given by the inner product
will have a square magnitude given by the inner product
Now if you take 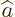 or
or 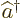 to the other side of an inner product,
it will change into the other one; the
to the other side of an inner product,
it will change into the other one; the  in the definitions (4)
will change sign. So the square magnitude of
in the definitions (4)
will change sign. So the square magnitude of 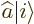 becomes
becomes
From the second form of the Hamiltonian in (5), it is seen that
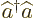 gives the number of energy quanta
gives the number of energy quanta  . And since the
state
. And since the
state 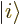 is normalized, the square magnitude of
is normalized, the square magnitude of 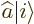 is
therefore
is
therefore  . That means that
. That means that
where  is some number of magnitude 1. Similarly
is some number of magnitude 1. Similarly
But note that you can always change the definition of an energy
eigenfunction by a constant of magnitude 1. That allows you, while
going up from 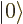 using
using 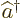 , to redefine each state so
that
, to redefine each state so
that 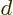 is 1. And if
is 1. And if 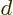 is always one, then so is
is always one, then so is  .
Otherwise
.
Otherwise 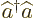 would not be
would not be  .
.
In the ground state, the expectation values of 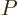 and
and  are zero,
while the expectation values of
are zero,
while the expectation values of 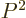 and
and 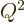 are equal to the
minimum
are equal to the
minimum  allowed by the uncertainty relation (3). The
derivations of these statements are the same as those for the harmonic
oscillator ground state in {D.13}.
allowed by the uncertainty relation (3). The
derivations of these statements are the same as those for the harmonic
oscillator ground state in {D.13}.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]() ,
,![]() ,
,![]() :
:![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]() ,
,![]() .
.![]() ;
;![]()
![]()
![]()
![]()
![]() .
.![]()
![]() .
.![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()