|
|
|
|
|
Next: 4.5 The Commutator |
|
It is a striking consequence of quantum mechanics that physical
quantities may not have a value. This occurs whenever the wave
function is not an eigenfunction of the quantity of interest. For
example, the ground state of the hydrogen atom is not an eigenfunction
of the position operator ![]() ,
,![]() -
-
However, it is possible to say something if the same measurement is
done on a large number of systems that are all the same before the
measurement. An example would be ![]() -
-expectation value,
of all
the measurements will be.
The expectation value is certainly not a replacement for the classical value of physical quantities. For example, for the hydrogen atom in the ground state, the expectation position of the electron is in the nucleus by symmetry. Yet because the nucleus is so small, measurements will never find it there! (The typical measurement will find it a distance comparable to the Bohr radius away.) Actually, that is good news, because if the electron would be in the nucleus as a classical particle, its potential energy would be almost minus infinity instead of the correct value of about -27 eV. It would be a very different universe. Still, having an expectation value is of course better than having no information at all.
The average discrepancy between the expectation value and the actual
measurements is called the standard deviation.
. In
the hydrogen atom example, where typically the electron is found a
distance comparable to the Bohr radius away from the nucleus, the
standard deviation in the ![]() -
-![]()
![]()
In general, the standard deviation is the quantitative measure for how much uncertainty there is in a physical value. If the standard deviation is very small compared to what you are interested in, it is probably OK to use the expectation value as a classical value. It is perfectly fine to say that the electron of the hydrogen atom that you are measuring is in your lab but it is not OK to say that it has countless electron volts of negative potential energy because it is in the nucleus.
This section discusses how to find expectation values and standard deviations after a brief introduction to the underlying ideas of statistics.
Key Points
- The expectation value is the average value obtained when doing measurements on a large number of initially identical systems. It is as close as quantum mechanics can come to having classical values for uncertain physical quantities.
- The standard deviation is how far the individual measurements on average deviate from the expectation value. It is the quantitative measure of uncertainty in quantum mechanics.
Since it seems to us humans as if, in Einstein's words, God is playing dice with the universe, it may be a worthwhile idea to examine the statistics of a die first.
For a fair die, each of the six numbers will, on average, show up a fraction 1/6 of the number of throws. In other words, each face has a probability of 1/6.
The average value of a large number of throws is called the
expectation value. For a fair die, the
expectation value is 3.5. After all, number 1 will show up in about
1/6 of the throws, as will numbers 2 through 6, so the average is
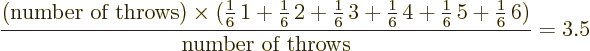
Note that the name expectation value
is very poorly
chosen. Even though the average value of a lot of throws will
be 3.5, you would surely not expect to throw 3.5. But it is
probably too late to change the name now.
The maximum possible deviation from the expectation value does of
course occur when you throw a 1 or a 6; the absolute deviation is then
![]()
![]()
![]()
![]()
However, the maximum possible deviation from the average is not a
useful concept for quantities like position, or for the energy levels
of the harmonic oscillator, where the possible values extend all the
way to infinity. So, instead of the maximum deviation from the
expectation value, some average deviation is better. The most
useful of those is called the “standard deviation”, denoted by ![]() .
.
![\begin{eqnarray*}
\sigma & = & \big[
{\textstyle\frac{1}{6}}(1-3.5)^2+{\textst...
...^2+{\textstyle\frac{1}{6}}(6-3.5)^2
\big]^{1/2} \\
& = & 1.71
\end{eqnarray*}](img734.gif)
Key Points
- The expectation value is obtained by summing the possible values times their probabilities.
- To get the standard deviation, first find the average square deviation from the expectation value, then take a square root of that.
Suppose you toss a coin a large number of times, and count heads as one, tails as two. What will be the expectation value?
Continuing this example, what will be the maximum deviation?
Continuing this example, what will be the standard deviation?
Have I got a die for you! By means of a small piece of lead integrated into its light-weight structure, it does away with that old-fashioned uncertainty. It comes up six every time! What will be the expectation value of your throws? What will be the standard deviation?
The expectation values of the operators of quantum mechanics are defined in the same way as those for the die.
Consider an arbitrary physical quantity, call it ![]() ,
,![]() .
.![]()
![]() ,
,![]()
![]() .
.
The equivalent of the face values of the die are the values that the
quantity ![]()
Next, the probabilities of getting those values are according to
quantum mechanics the square magnitudes of the coefficients when the
wave function is written in terms of the eigenfunctions of ![]() .
.![]() ,
,![]() ,
,![]() ,
,![]() ,
,
The expectation value is written as ![]() ,
,![]() ,
,
Of course, the eigenfunctions might be numbered using multiple
indices; that does not really make a difference.
For example, the eigenfunctions ![]()
Key Points
- The expectation value of a physical quantity is found by summing its eigenvalues times the probability of measuring that eigenvalue.
- To find the probabilities of the eigenvalues, the wave function
can be written in terms of the eigenfunctions of the physical quantity. The probabilities will be the square magnitudes of the coefficients of the eigenfunctions.
The 2![]()
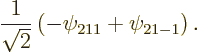
Continuing the previous question, what are the standard deviations in energy, square angular momentum, and ![]()
The procedure described in the previous section to find the expectation value of a quantity is unwieldy: it requires that first the eigenfunctions of the quantity are found, and next that the wave function is written in terms of those eigenfunctions. There is a quicker way.
Assume that you want to find the expectation value, ![]()
![]() ,
,![]()
![]() .
.
| (4.43) |
leaving outfrom the inner product bracket. The reason that
The simplified expression for the expectation value can also be used
to find the standard deviation, ![]()
![]() :
:
Key Points
- The expectation value of a quantity
with operator can be found as .
- Similarly, the standard deviation can be found using the expression
.
The 2![]()
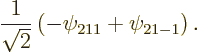
Continuing the previous question, evaluate the standard deviations in energy, square angular momentum, and ![]()
![]()
This section gives some examples of expectation values and standard deviations for known wave functions.
First consider the expectation value of the energy of the hydrogen
atom in its ground state ![]() .
.![]()
![]()
![]() 1
1![]() ,
,
Clearly, if all measurements return the value ![]() ,
,![]()
![]() .
.![]() ,
,![]()
It is instructive to check those conclusions using the simplified
expressions for expectation values and standard deviations from the
previous subsection. The expectation value can be found as:
The standard deviation
In general,
If the wave function is an eigenfunction of the measured variable, the expectation value will be the eigenvalue, and the standard deviation will be zero.To get uncertainty, in other words, a nonzero standard deviation, the wave function should not be an eigenfunction of the quantity being measured.
For example, the ground state of the hydrogen atom is an energy
eigenfunction, but not an eigenfunction of the position operators.
The expectation value for the position coordinate ![]()

The position coordinates ![]()
![]()
![]()
![]()
In fact, all basic energy eigenfunctions ![]()
![]()
![]()
But don’t really expect to ever find the electron in the
negligible small nucleus! You will find it at locations that are on
average one standard deviation away from it. For example, in
the ground state
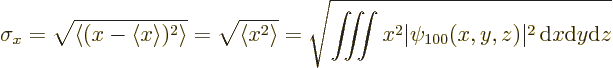
If you actually do the integral above, (it is not difficult in
spherical coordinates,) you find that the standard deviation in ![]()
![]() -
-![]()
![]()
The expectation value of linear momentum in the ground state can be
found from the linear momentum operator ![]()
![]()
![]()
![]()
![]() :
:

More generally, the expectation value for linear momentum is zero for all the energy eigenfunctions; that is a consequence of Ehrenfest's theorem covered in chapter 7.2.1. The standard deviations are again nonzero, so that linear momentum is uncertain like position is.
All these observations carry over in the same way to the
eigenfunctions ![]()
If combinations of energy eigenfunctions are considered, it changes. Such combinations may have nontrivial expectation positions and linear momenta. A discussion will have to wait until chapter 7.
Key Points
- Examples of definite and uncertain quantities were given for example wave functions.
- A quantity has a definite value when the wave function is an eigenfunction of the operator corresponding to that quantity.