11.5 The Canon­i­cal Prob­a­bil­ity Dis­tri­b­u­tion

The par­ti­cle en­ergy dis­tri­b­u­tion func­tions in the pre­vi­ous sec­tion were de­rived as­sum­ing that the en­ergy is given. In quan­tum-me­chan­i­cal terms, it was as­sumed that the en­ergy had a def­i­nite value. How­ever, that can­not re­ally be right, for one be­cause of the en­ergy-time un­cer­tainty prin­ci­ple.

As­sume for a sec­ond that a lot of boxes of par­ti­cles are care­fully pre­pared, all with a sys­tem en­ergy as pre­cise as it can be made. And that all these boxes are then stacked to­gether into one big sys­tem. In the com­bined sys­tem of stacked boxes, the en­ergy is pre­sum­ably quite un­am­bigu­ous, since the ran­dom er­rors are likely to can­cel each other, rather than add up sys­tem­at­i­cally. In fact, sim­plis­tic sta­tis­tics would ex­pect the rel­a­tive er­ror in the en­ergy of the com­bined sys­tem to de­crease like the square root of the num­ber of boxes.

But for the care­fully pre­pared in­di­vid­ual boxes, the fu­ture of their lack of en­ergy un­cer­tainty is much bleaker. Surely a sin­gle box in the stack may ran­domly ex­change a bit of en­ergy with the other boxes. Of course, when a box ac­quires much more en­ergy than the oth­ers, the ex­change will no longer be ran­dom, but al­most cer­tainly go from the hot­ter box to the cooler ones. Still, it seems un­avoid­able that quite a lot of un­cer­tainty in the en­ergy of the in­di­vid­ual boxes would re­sult. The boxes still have a pre­cise tem­per­a­ture, be­ing in ther­mal equi­lib­rium with the larger sys­tem, but no longer a pre­cise en­ergy.

Then the ap­pro­pri­ate way to de­scribe the in­di­vid­ual boxes is no longer in terms of given en­ergy, but in terms of prob­a­bil­i­ties. The proper ex­pres­sion for the prob­a­bil­i­ties is de­duced in de­riva­tion {D.58}. It turns out that when the tem­per­a­ture $T$, but not the en­ergy of a sys­tem is cer­tain, the sys­tem en­ergy eigen­func­tions $\psi^{\rm S}_q$ can be as­signed prob­a­bil­i­ties of the form

$$\fbox{$\displaystyle P_q = \frac{1}{Z} e^{-{\vphantom' E}^{\rm S}_q/{k_{\rm B}}T} $} %$$ (11.4)

where $k_{\rm B}$ $\vphantom0\raisebox{1.5pt}{$=$}$ 1.380 65 10$\POW9,{-23}$ J/K is the Boltz­mann con­stant. This equa­tion for the prob­a­bil­i­ties is called the Gibbs canon­i­cal prob­a­bil­ity dis­tri­b­u­tion. Feyn­man [18, p. 1] calls it the sum­mit of sta­tis­ti­cal me­chan­ics.

The ex­po­nen­tial by it­self is called the “Boltz­mann fac­tor.” The nor­mal­iza­tion fac­tor $Z$, which makes sure that the prob­a­bil­i­ties all to­gether sum to one, is called the “par­ti­tion func­tion.” It equals

$$\fbox{$\displaystyle Z = \sum_{{\rm all}\;q} e^{-{\vphantom' E}^{\rm S}_q/{k_{\rm B}}T} $} %$$ (11.5)

You might won­der why a mere nor­mal­iza­tion fac­tor war­rants its own name. It turns out that if an an­a­lyt­i­cal ex­pres­sion for the par­ti­tion func­tion $Z(T,V,I)$ is avail­able, var­i­ous quan­ti­ties of in­ter­est may be found from it by tak­ing suit­able par­tial de­riv­a­tives. Ex­am­ples will be given in sub­se­quent sec­tions.

The canon­i­cal prob­a­bil­ity dis­tri­b­u­tion con­forms to the fun­da­men­tal as­sump­tion of quan­tum sta­tis­tics that eigen­func­tions of the same en­ergy have the same prob­a­bil­ity. How­ever, it adds that for sys­tem eigen­func­tions with dif­fer­ent en­er­gies, the higher en­er­gies are less likely. Mas­sively less likely, to be sure, be­cause the sys­tem en­ergy ${\vphantom' E}^{\rm S}_q$ is a macro­scopic en­ergy, while the en­ergy ${k_{\rm B}}T$ is a mi­cro­scopic en­ergy level, roughly the ki­netic en­ergy of a sin­gle atom in an ideal gas at that tem­per­a­ture. So the Boltz­mann fac­tor de­cays ex­tremely rapidly with en­ergy.

Fig­ure 11.7: Prob­a­bil­i­ties of shelf-num­ber sets for the sim­ple 64 par­ti­cle model sys­tem if there is un­cer­tainty in en­ergy. More prob­a­ble shelf-num­ber dis­tri­b­u­tions are shown darker. Left: iden­ti­cal bosons, mid­dle: dis­tin­guish­able par­ti­cles, right: iden­ti­cal fermi­ons. The tem­per­a­ture is the same as in the pre­vi­ous two fig­ures.

So, what hap­pens to the sim­ple model sys­tem from sec­tion 11.3 when the en­ergy is no longer cer­tain, and in­stead the prob­a­bil­i­ties are given by the canon­i­cal prob­a­bil­ity dis­tri­b­u­tion? The an­swer is in the mid­dle graphic of fig­ure 11.7. Note that there is no longer a need to limit the dis­played en­er­gies; the strong ex­po­nen­tial de­cay of the Boltz­mann fac­tor takes care of killing off the high en­ergy eigen­func­tions. The rapid growth of the num­ber of eigen­func­tions does re­main ev­i­dent at lower en­er­gies where the Boltz­mann fac­tor has not yet reached enough strength.

There is still an oblique en­ergy line in fig­ure 11.7, but it is no longer lim­it­ing en­ergy; it is merely the en­ergy at the most prob­a­ble shelf oc­cu­pa­tion num­bers. Equiv­a­lently, it is the ex­pec­ta­tion en­ergy of the sys­tem, de­fined fol­low­ing the ideas of chap­ter 4.4.1 as

$$\langle E \rangle \equiv \sum_{{\rm all}\;q} P_q {\vphantom' E}^{\rm S}_q \equiv E$$

be­cause for a macro­scopic sys­tem size, the most prob­a­ble and ex­pec­ta­tion val­ues are the same. That is a di­rect re­sult of the black blob col­laps­ing to­wards a sin­gle point for in­creas­ing sys­tem size: in a macro­scopic sys­tem, es­sen­tially all sys­tem eigen­func­tions have the same macro­scopic prop­er­ties.

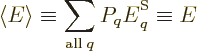
In ther­mo­dy­nam­ics, the ex­pec­ta­tion en­ergy is called the in­ter­nal en­ergy and in­di­cated by $E$ or $U$. This book will use $E$, drop­ping the an­gu­lar brack­ets. The dif­fer­ence in no­ta­tion from the sin­gle-par­ti­cle/shelf/sys­tem en­er­gies is that the in­ter­nal en­ergy is plain $E$ with no sub­scripts or su­per­scripts.

Fig­ure 11.7 also shows the shelf oc­cu­pa­tion num­ber prob­a­bil­i­ties if the ex­am­ple 64 par­ti­cles are not dis­tin­guish­able, but iden­ti­cal bosons or iden­ti­cal fermi­ons. The most prob­a­ble shelf num­bers are not the same, since bosons and fermi­ons have dif­fer­ent num­bers of eigen­func­tions than dis­tin­guish­able par­ti­cles, but as the fig­ure shows, the ef­fects are not dra­matic at the shown tem­per­a­ture, ${k_{\rm B}}T$ $\vphantom0\raisebox{1.5pt}{$=$}$ 1.85 in the ar­bi­trary en­ergy units.