| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
11.13 Microscopic Meaning of the Variables
The new variables introduced in the previous section assume the
temperature to be defined, hence there must be thermodynamic
equilibrium in some meaningful sense. That is important for
identifying their microscopic descriptions, since the canonical
expression 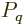

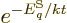

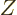 can be used for the
probabilities of the energy eigenfunctions.
can be used for the
probabilities of the energy eigenfunctions.
Consider first the Helmholtz free energy:
This can be simplified by taking apart the logarithm, and noting that
the probabilities must sum to one, 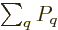
 1, to give
1, to give
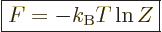 |
(11.40) |
That makes strike three for the partition function 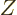 , since it
already was able to produce the internal energy
, since it
already was able to produce the internal energy  ,
(11.7), and the pressure
,
(11.7), and the pressure 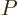 , (11.9).
Knowing
, (11.9).
Knowing 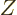 as a function of volume
as a function of volume  , temperature
, temperature 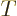 ,
and number of particles
,
and number of particles  is all that is needed to figure out the
other variables. Indeed, knowing
is all that is needed to figure out the
other variables. Indeed, knowing  is just as good as knowing the
entropy
is just as good as knowing the
entropy 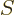 , since
, since 

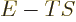 . It illustrates why
the partition function is much more valuable than you might expect
from a mere normalization factor of the probabilities.
. It illustrates why
the partition function is much more valuable than you might expect
from a mere normalization factor of the probabilities.
For the Gibbs free energy, add 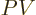 from (11.9):
from (11.9):
![\begin{displaymath}
\fbox{$\displaystyle
G
=
- k_{\rm B}T
\left[
\ln Z - V \left(\frac{\partial \ln Z}{\partial V}\right)_T
\right]
$} %
\end{displaymath}](img2525.gif) |
(11.41) |
Dividing by the number of moles gives the molar specific Gibbs energy
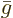 , equal to the chemical potential
, equal to the chemical potential 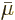 .
.
How about showing that this chemical potential is the same one as in
the Maxwell-Boltzmann, Fermi-Dirac, and Bose-Einstein distribution
functions for weakly interacting particles? It is surprisingly
difficult to show it; in fact, it cannot be done for distinguishable
particles for which the entropy does not exist. It further appears
that the best way to get the result for bosons and fermions is to
elaborately re-derive the two distributions from scratch, each
separately, using a new approach. Note that they were already derived
twice earlier, once for given system energy, and once for the
canonical probability distribution. So the dual derivations in
{D.61} make three. Please note that whatever this book
tells you thrice is absolutely true.
![]()
![]()
![]()
![]()
![]()
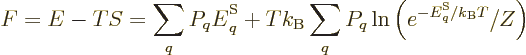
![]()