| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
Subsections
11.14 Application to Particles in a Box
This section applies the ideas developed in the previous sections to
weakly interacting particles in a box. This allows some of the
details of the shelves
in figures 11.1
through 11.3 to be filled in for a concrete case.
For particles in a macroscopic box, the single-particle energy levels
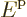 are so closely spaced that they can be taken to be continuously
varying. The one exception is the ground state when Bose-Einstein
condensation occurs; that will be ignored for now. In continuum
approximation, the number of single-particle energy states in a
macroscopically small energy range
are so closely spaced that they can be taken to be continuously
varying. The one exception is the ground state when Bose-Einstein
condensation occurs; that will be ignored for now. In continuum
approximation, the number of single-particle energy states in a
macroscopically small energy range 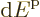 is approximately,
following (6.6),
is approximately,
following (6.6),
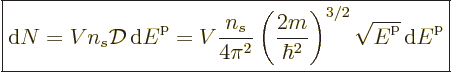 |
(11.42) |
Here 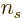

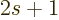 is the number of spin states.
is the number of spin states.
Now according to the derived distributions, the number of particles in
a single energy state at energy 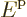 is
is
where the plus sign applies for fermions and the minus sign for
bosons. The term can be ignored completely for distinguishable
particles.
To get the total number of particles, just integrate the particles per
state 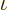 over all states:
over all states:
and to get the total energy, integrate the energy of each
single-particle state times the number of particles in that state over
all states:
The expression for the number of particles can be nondimensionalized
by rearranging and taking a root to give
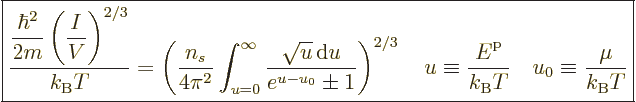 |
(11.43) |
Note that the left hand side is a nondimensional ratio of a typical
quantum microscopic energy, based on the average particle spacing
![$\sqrt[3]{V/I}$](img2533.gif) , to the typical classical microscopic energy
, to the typical classical microscopic energy
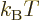 . This ratio is a key nondimensional number governing
weakly interacting particles in a box. To put the typical quantum
energy into context, a single particle in its own volume of size
. This ratio is a key nondimensional number governing
weakly interacting particles in a box. To put the typical quantum
energy into context, a single particle in its own volume of size


 would have a ground state energy
would have a ground state energy
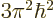

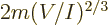 .
.
Some references, [4], define a “thermal de Broglie wavelength” 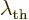 by writing
the classical microscopic energy
by writing
the classical microscopic energy 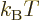 in a quantum-like way:
in a quantum-like way:
In some simple cases, you can think of this as roughly the quantum
wavelength corresponding to the momentum of the particles. It allows
various results that depend on the nondimensional ratio of energies
to be reformulated in terms of a nondimensional ratio of lengths,
as in
Since the ratio of energies is fully equivalent, and has an
unambiguous meaning, this book will refrain from making theory harder
than needed by defining superfluous quantities. But in practice,
thinking in terms of numerical values that are lengths is likely to be
more intuitive than energies, and then the numerical value of the
thermal wavelength would be the one to keep in mind.
Note that (11.43) provides a direct relationship between the
ratio of typical quantum/classical energies on one side, and
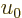 , the ratio of atomic chemical potential
, the ratio of atomic chemical potential  to typical
classical microscopic energy
to typical
classical microscopic energy 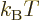 on the other side. While the
two energy ratios are not the same, (11.43) makes them
equivalent for systems of weakly interacting particles in boxes. Know
one and you can in principle compute the other.
on the other side. While the
two energy ratios are not the same, (11.43) makes them
equivalent for systems of weakly interacting particles in boxes. Know
one and you can in principle compute the other.
The expression for the system energy may be nondimensionalized in
a similar way to get
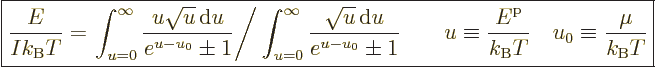 |
(11.44) |
The integral in the bottom arises when getting rid of the ratio of
energies that forms using (11.43).
The quantity in the left hand side is the nondimensional ratio of the
actual system energy over the system energy if every particle had the
typical classical energy 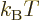 . It too is a unique function
of
. It too is a unique function
of 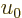 , and as a consequence, also of the ratio of typical
microscopic quantum and classical energies.
, and as a consequence, also of the ratio of typical
microscopic quantum and classical energies.
11.14.1 Bose-Einstein condensation
Bose-Einstein condensation is said to have occurred when in a
macroscopic system the number of bosons in the ground state becomes a
finite fraction of the number of particles  . It happens when
the temperature is lowered sufficiently or the particle density is
increased sufficiently or both.
. It happens when
the temperature is lowered sufficiently or the particle density is
increased sufficiently or both.
According to derivation {D.57}, the number of particles in the
ground state is given by
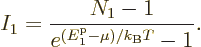 |
(11.45) |
In order for this to become a finite fraction of the large number of
particles  of a macroscopic system, the denominator must become
extremely small, hence the exponential must become extremely close to
one, hence
of a macroscopic system, the denominator must become
extremely small, hence the exponential must become extremely close to
one, hence  must come extremely close to the lowest energy level
must come extremely close to the lowest energy level
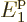 . To be precise,
. To be precise, 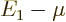 must be small of order
must be small of order
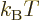

 ; smaller than the classical microscopic
energy by the humongous factor
; smaller than the classical microscopic
energy by the humongous factor  . In addition, for a
macroscopic system of weakly interacting particles in a box,
. In addition, for a
macroscopic system of weakly interacting particles in a box, 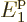 is extremely close to zero, (it is smaller than the microscopic
quantum energy defined above by a factor
is extremely close to zero, (it is smaller than the microscopic
quantum energy defined above by a factor 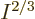 .) So
condensation occurs when
.) So
condensation occurs when 
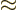
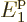
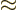 0, the
approximations being extremely close. If the ground state is unique,
0, the
approximations being extremely close. If the ground state is unique,

 1, Bose-Einstein condensation simply occurs when
1, Bose-Einstein condensation simply occurs when 

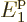
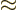 0.
0.
You would therefore expect that you can simply put 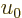



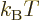 to zero in the integrals (11.43) and
(11.44). However, if you do so (11.43) fails to
describe the number of particles in the ground state; it only gives
the number of particles
to zero in the integrals (11.43) and
(11.44). However, if you do so (11.43) fails to
describe the number of particles in the ground state; it only gives
the number of particles  not in the ground state:
not in the ground state:
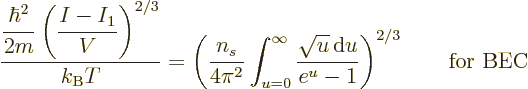 |
(11.46) |
To see that the number of particles in the ground state is indeed not
included in the integral, note that while the integrand does become
infinite when 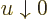 , it becomes infinite proportionally
to 1/
, it becomes infinite proportionally
to 1/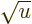 , which integrates as proportional to
, which integrates as proportional to
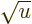 , and
, and 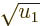

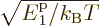 is
vanishingly small, not finite. Arguments given in derivation
{D.57} do show that the only significant error occurs
for the ground state; the above integral does correctly approximate
the number of particles not in the ground state when condensation has
occurred.
is
vanishingly small, not finite. Arguments given in derivation
{D.57} do show that the only significant error occurs
for the ground state; the above integral does correctly approximate
the number of particles not in the ground state when condensation has
occurred.
The value of the integral can be found in mathematical handbooks,
[41, p. 201, with typo], as
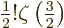 with
with 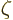 the so-called Riemann
zeta function, due to, who else, Euler. Euler showed that it is equal
to a product of terms ranging over all prime numbers, but you do not
want to know that. All you want to know is that
the so-called Riemann
zeta function, due to, who else, Euler. Euler showed that it is equal
to a product of terms ranging over all prime numbers, but you do not
want to know that. All you want to know is that

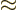 2.612 and that
2.612 and that 

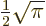 .
.
The Bose-Einstein temperature 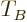 is the temperature at which
Bose-Einstein condensation starts. That means it is the
temperature for which
is the temperature at which
Bose-Einstein condensation starts. That means it is the
temperature for which 
 0 in the expression above, giving
0 in the expression above, giving
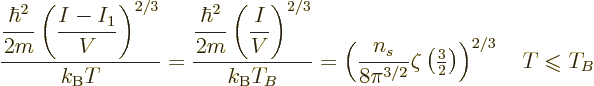 |
(11.47) |
It implies that for a given system of bosons, at Bose-Einstein
condensation there is a fixed numerical ratio between the microscopic
quantum energy based on particle density and the classical microscopic
energy 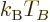 . That also illustrates the point made at the
beginning of this subsection that both changes in temperature and
changes in particle density can produce Bose-Einstein condensation.
. That also illustrates the point made at the
beginning of this subsection that both changes in temperature and
changes in particle density can produce Bose-Einstein condensation.
The first equality in the equation above can be cleaned up to give the
fraction of bosons in the ground state as:
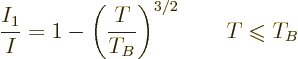 |
(11.48) |
11.14.2 Fermions at low temperatures
Another application of the integrals (11.43) and
(11.44) is to find the Fermi energy 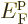 and internal
energy
and internal
energy  of a system of weakly interacting fermions for vanishing
temperature.
of a system of weakly interacting fermions for vanishing
temperature.
For low temperatures, the nondimensional energy ratio 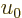



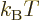 blows up, since
blows up, since 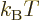 becomes zero and the chemical
potential
becomes zero and the chemical
potential  does not;
does not;  becomes the Fermi energy
becomes the Fermi energy
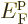 , chapter 6.10. To deal with the blow
up, the integrals can be rephrased in terms of
, chapter 6.10. To deal with the blow
up, the integrals can be rephrased in terms of 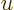

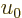

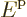

 , which does not blow up.
, which does not blow up.
In particular, the ratio (11.43) involving the typical
microscopic quantum energy can be rewritten by taking a factor
 out of the integral and root and to the other side to
give:
out of the integral and root and to the other side to
give:
Now since 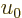 is large, the exponential in the denominator becomes
extremely large for
is large, the exponential in the denominator becomes
extremely large for 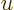

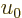
 1, making the integrand negligibly
small. Therefore the upper limit of integration can be limited to
1, making the integrand negligibly
small. Therefore the upper limit of integration can be limited to
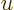

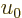
 1. In that range, the exponential is vanishingly small,
except for a negligibly small range around
1. In that range, the exponential is vanishingly small,
except for a negligibly small range around 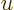

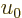
 1, so it can
be ignored. That gives
1, so it can
be ignored. That gives
It follows that the Fermi energy is
Physicist like to define a “Fermi temperature” as the temperature where the classical
microscopic energy 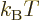 becomes equal to the Fermi energy. It is
becomes equal to the Fermi energy. It is
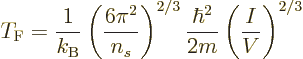 |
(11.49) |
It may be noted that except for the numerical factor, the expression
for the Fermi temperature 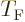 is the same as that for the
Bose-Einstein condensation temperature
is the same as that for the
Bose-Einstein condensation temperature 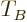 given in the previous
subsection.
given in the previous
subsection.
Electrons have 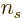
 2. For the valence electrons in typical metals,
the Fermi temperatures are in the order of ten thousands of degrees
Kelvin. The metal will melt before it is reached. The valence
electrons are pretty much the same at room temperature as they are at
absolute zero.
2. For the valence electrons in typical metals,
the Fermi temperatures are in the order of ten thousands of degrees
Kelvin. The metal will melt before it is reached. The valence
electrons are pretty much the same at room temperature as they are at
absolute zero.
The integral (11.44) can be integrated in the same way and
then shows that 

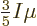

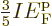 . In short, at absolute zero, the average
energy per particle is
. In short, at absolute zero, the average
energy per particle is 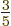 times
times 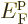 , the
maximum single-particle energy.
, the
maximum single-particle energy.
It should be admitted that both of the results in this subsection have
been obtained more simply in chapter 6.10. However, the
analysis in this subsection can be used to find the corrected
expressions when the temperature is fairly small but not zero,
{D.62}, or for any temperature by brute-force
numerical integration. One result is the specific heat at constant
volume of the free-electron gas for low temperatures:
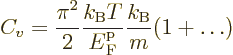 |
(11.50) |
where 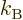

 is the gas constant
is the gas constant  . All low-temperature
expansions proceed in powers of
. All low-temperature
expansions proceed in powers of 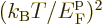 , so
the dots in the expression for
, so
the dots in the expression for 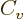 above are of that order. The
specific heat vanishes at zero temperature and is typically small.
above are of that order. The
specific heat vanishes at zero temperature and is typically small.
11.14.3 A generalized ideal gas law
While the previous subsections produced a lot of interesting
information about weakly interacting particles near absolute zero, how
about some info about conditions that you can check in a T-shirt? And
how about something mathematically simple, instead of elaborate
integrals that produce weird functions?
Well, there is at least one. By definition, (11.8), the
pressure is the expectation value of 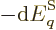

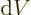 where the
where the
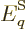 are the system energy eigenvalues. For weakly interacting
particles in a box, chapter 6.2 found that the single
particle energies are inversely proportional to the squares of the
linear dimensions of the box, which means proportional to
are the system energy eigenvalues. For weakly interacting
particles in a box, chapter 6.2 found that the single
particle energies are inversely proportional to the squares of the
linear dimensions of the box, which means proportional to
 . Then so are the system energy eigenfunctions, since
they are sums of single-particle ones:
. Then so are the system energy eigenfunctions, since
they are sums of single-particle ones: 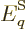

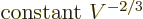 Differentiating produces
Differentiating produces
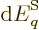

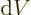

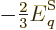

 and taking the
expectation value
and taking the
expectation value
 |
(11.51) |
This expression is valid for weakly interacting bosons and fermions
even if the symmetrization requirements cannot be ignored.
11.14.4 The ideal gas
The weakly interacting particles in a box can be approximated as an
ideal gas if the number of particles is so small, or the box so large,
that the average number of particles in an energy state is much less
than one.
Since the number of particles per energy state is given by
ideal gas conditions imply that the exponential must be much greater
than one, and then the  can be ignored. That means that the
difference between fermions and bosons, which accounts for the
can be ignored. That means that the
difference between fermions and bosons, which accounts for the
 , can be ignored for an ideal gas. Both can be
approximated by the distribution derived for distinguishable
particles.
, can be ignored for an ideal gas. Both can be
approximated by the distribution derived for distinguishable
particles.
The energy integral (11.44) can now easily be done; the
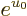 factor divides away and an integration by parts in the
numerator produces
factor divides away and an integration by parts in the
numerator produces 

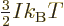 . Plug it into the
generalized ideal gas law (11.51) to get the normal “ideal gas law”
. Plug it into the
generalized ideal gas law (11.51) to get the normal “ideal gas law”
 |
(11.52) |
Also, following (11.34),
but note that these formulae are specific to the simplistic ideal
gases described by the model, (like noble gases.) For ideal gases
with more complex molecules, like air, the specific heats are not
constants, but vary with temperature, as discussed in section
11.15.
The ideal gas equation is identical to the one derived in classical
physics. That is important since it establishes that what was defined
to be the temperature in this chapter is in fact the ideal gas
temperature that classical physics defines.
The integral (11.43) can be done using integration by parts
and a result found in the notations under !
. It gives
an expression for the single-particle chemical potential  :
:
Note that the argument of the logarithm is essentially the ratio
between the classical microscopic energy and the quantum microscopic
energy based on average particle spacing. This ratio has to be big
for an accurate ideal gas, to get the exponential in the particle
energy distribution 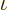 to be big.
to be big.
Next is the specific entropy  . Recall that the chemical
potential is just the Gibbs free energy. By the definition of the
Gibbs free energy, the specific entropy
. Recall that the chemical
potential is just the Gibbs free energy. By the definition of the
Gibbs free energy, the specific entropy  equals
equals 

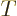 .
Now the specific Gibbs energy is just the Gibbs energy per unit mass,
in other words,
.
Now the specific Gibbs energy is just the Gibbs energy per unit mass,
in other words, 

 while
while 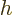

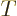

 as above. So
as above. So
![\begin{displaymath}
\fbox{$\displaystyle
s =
C_v
\ln
\left[
{k_{\rm B}}T\l...
...}\right.
\left(\frac{I}{V}\right)^{2/3}
\right]
+ C_p
$} %
\end{displaymath}](img2582.gif) |
(11.53) |
In terms of classical thermodynamics, 

 is
is  times the
specific volume
times the
specific volume 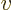 . So classical thermodynamics takes the
logarithm above apart as
. So classical thermodynamics takes the
logarithm above apart as
and then promptly forgets about the constant, damn units.
11.14.5 Blackbody radiation
This section takes a closer look at blackbody radiation, discussed
earlier in chapter 6.8. Blackbody radiation is the basic
model for absorption and emission of electromagnetic radiation.
Electromagnetic radiation includes light and a wide range of other
radiation, like radio waves, microwaves, and X-rays. All surfaces
absorb and emit radiation; otherwise we would not see anything. But
black
surfaces are the most easy to understand
theoretically.
No, a black body need not look black. If its temperature is high
enough, it could look like the sun. What defines an ideal black body
is that it absorbs, (internalizes instead of reflects,) all radiation
that hits it. But it may be emitting its own radiation at the same
time. And that makes a difference. If the black body is cool, you
will need your infrared camera to see it; it would look really black
to the eye. It is not reflecting any radiation, and it is not
emitting any visible amount either. But if it is at the temperature
of the sun, better take out your sunglasses. It is still absorbing
all radiation that hits it, but it is emitting large amounts of its
own too, and lots of it in the visible range.
So where do you get a nearly perfectly black surface? Matte black
paint? A piece of blackboard? Soot? Actually, pretty much all
materials will reflect in some range of wave lengths. You get the
blackest surface by using no material at all. Take a big box and
paint its interior the blackest you can. Close the box, then drill a
very tiny hole in its side. From the outside, the area of the hole
will be truly, absolutely black. Whatever radiation enters there is
gone. Still, when you heat the box to very high temperatures, the
hole will shine bright.
While any radiation entering the hole will most surely be absorbed
somewhere inside, the inside of the box itself is filled with
electromagnetic radiation, like a gas of photons, produced by the hot
inside surface of the box. And some of those photons will manage to
escape through the hole, making it shine.
The amount of photons in the box may be computed from the
Bose-Einstein distribution with a few caveats. The first is that
there is no limit on the number of photons; photons will be created or
absorbed by the box surface to achieve thermal equilibrium at whatever
level is most probable at the given temperature. This means the
chemical potential  of the photons is zero, as you can check from
the derivations in notes {D.57} and
{D.58}.
of the photons is zero, as you can check from
the derivations in notes {D.57} and
{D.58}.
The second caveat is that the usual density of states (6.6)
is nonrelativistic. It does not apply to photons, which move at the
speed of light. For photons you must use the density of modes
(6.7).
The third caveat is that there are only two independent spin states
for a photon. As a spin-one particle you would expect that photons
would have the spin values 0 and  , but the zero value does
not occur in the direction of propagation, addendum
{A.21.6}. Therefore the number of independent states
that exist is two, not three. A different way to understand this is
classical: the electric field can only oscillate in the two
independent directions normal to the direction of propagation,
(13.10); oscillation in the direction of propagation
itself is not allowed by Maxwell’s laws because it would make the
divergence of the electric field nonzero. The fact that there are
only two independent states has already been accounted for in the
density of modes (6.7).
, but the zero value does
not occur in the direction of propagation, addendum
{A.21.6}. Therefore the number of independent states
that exist is two, not three. A different way to understand this is
classical: the electric field can only oscillate in the two
independent directions normal to the direction of propagation,
(13.10); oscillation in the direction of propagation
itself is not allowed by Maxwell’s laws because it would make the
divergence of the electric field nonzero. The fact that there are
only two independent states has already been accounted for in the
density of modes (6.7).
The energy per unit box volume and unit frequency range found under
the above caveats is Planck’s blackbody spectrum already given in
chapter 6.8:
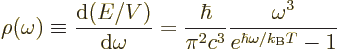 |
(11.54) |
The expression for the total internal energy per unit volume is called
the “Stefan-Boltzmann formula.” It is found by integration of
Planck’s spectrum over all frequencies just like for the
Stefan-Boltzmann law in chapter 6.8:
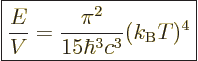 |
(11.55) |
The number of particles may be found similar to the energy, by
dropping the 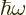 energy per particle from the integral. It
is, [41, 36.24, with typo]:
energy per particle from the integral. It
is, [41, 36.24, with typo]:
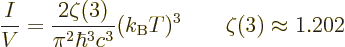 |
(11.56) |
Taking the ratio with (11.55), the average energy per photon
may be found:
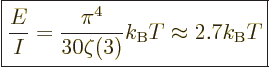 |
(11.57) |
The temperature has to be roughly 9 000 K for the average photon to
become visible light. That is one reason a black body will look black
at a room temperature of about 300 K. The solar surface has a
temperature of about 6 000 K, so the visible light photons it emits
are more energetic than average, but there are still plenty of them.
The entropy 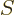 of the photon gas follows from integrating
of the photon gas follows from integrating
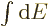

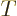 using (11.55), starting from absolute zero and
keeping the volume constant:
using (11.55), starting from absolute zero and
keeping the volume constant:
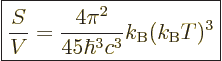 |
(11.58) |
Dividing by (11.56) shows the average entropy per photon to be
 |
(11.59) |
independent of temperature.
The generalized ideal gas law (11.51) does not apply to the
pressure exerted by the photon gas, because the energy of the photons
is 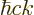 and that is proportional to the wave number instead of its
square. The corrected expression is:
and that is proportional to the wave number instead of its
square. The corrected expression is:
 |
(11.60) |
11.14.6 The Debye model
To explain the heat capacity of simple solids, Debye modeled the
energy in the crystal vibrations very much the same way as the photon
gas of the previous subsection. This subsection briefly outlines the
main ideas.
For electromagnetic waves propagating with the speed of light
 , substitute acoustical waves propagating with the speed of
sound
, substitute acoustical waves propagating with the speed of
sound 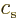 . For photons with energy
. For photons with energy
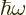 , substitute phonons with energy
, substitute phonons with energy
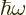 . Since unlike electromagnetic waves, sound waves
can vibrate in the direction of wave propagation, for the
number of spin states substitute
. Since unlike electromagnetic waves, sound waves
can vibrate in the direction of wave propagation, for the
number of spin states substitute 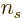
 3 instead of 2; in other
words, just multiply the various expressions for photons by 1.5.
3 instead of 2; in other
words, just multiply the various expressions for photons by 1.5.
The critical difference for solids is that the number of modes, hence
the frequencies, is not infinitely large. Since each individual atom
has three degrees of freedom (it can move in three individual
directions), there are 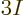 degrees of freedom, and reformulating the
motion in terms of acoustic waves does not change the number of
degrees of freedom. The shortest wave lengths will be comparable to
the atom spacing, and no waves of shorter wave length will exist. As
a result, there will be a highest frequency
degrees of freedom, and reformulating the
motion in terms of acoustic waves does not change the number of
degrees of freedom. The shortest wave lengths will be comparable to
the atom spacing, and no waves of shorter wave length will exist. As
a result, there will be a highest frequency 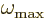 .
The “Debye temperature”
.
The “Debye temperature” 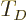 is defined as the temperature at which
the typical classical microscopic energy
is defined as the temperature at which
the typical classical microscopic energy 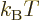 becomes equal to the
maximum quantum microscopic energy
becomes equal to the
maximum quantum microscopic energy 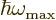
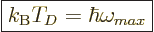 |
(11.61) |
The expression for the internal energy becomes, from (6.11)
times 1.5:
 |
(11.62) |
If the temperatures are very low the exponential will make the
integrand zero except for very small frequencies. Then the upper
limit is essentially infinite compared to the range of integration.
That makes the energy proportional to 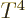 just like for the photon
gas and the heat capacity is therefore proportional to
just like for the photon
gas and the heat capacity is therefore proportional to 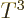 .
At the other extreme, when the temperature is large, the exponential
in the bottom can be expanded in a Taylor series and the energy
becomes proportional to
.
At the other extreme, when the temperature is large, the exponential
in the bottom can be expanded in a Taylor series and the energy
becomes proportional to 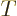 , making the heat capacity constant.
, making the heat capacity constant.
The maximum frequency, hence the Debye temperature, can be found from
the requirement that the number of modes is 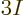 , to be applied
by integrating (6.7), or an empirical value can be used to
improve the approximation for whatever temperature range is of
interest. Literature values are often chosen to approximate the low
temperature range accurately, since the model works best for low
temperatures. If integration of (6.7) is used at high
temperatures, the law of Dulong and Petit results, as described in
section 11.15.
, to be applied
by integrating (6.7), or an empirical value can be used to
improve the approximation for whatever temperature range is of
interest. Literature values are often chosen to approximate the low
temperature range accurately, since the model works best for low
temperatures. If integration of (6.7) is used at high
temperatures, the law of Dulong and Petit results, as described in
section 11.15.
More sophisticated versions of the analysis exist to account for some
of the very nontrivial differences between crystal vibrations and
electromagnetic waves. They will need to be left to literature.
![]()
![]()
![]()
![]()


![]()
![]()
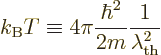
![\begin{displaymath}
\frac{\displaystyle \frac{\hbar^2}{2m}\left(\frac{I}{V}\rig...
...\left[\frac{\lambda_{\rm th}}{\left(V/I\right)^{1/3}}\right]^2
\end{displaymath}](img2538.gif)
![]() ,
,![]()
![]()
![]() .
.![]() ,
,![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
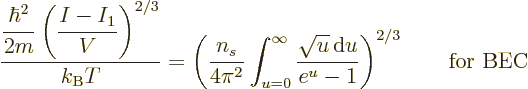
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
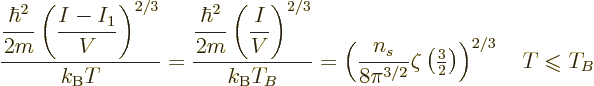
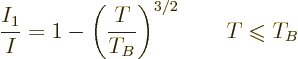
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![\begin{displaymath}
\frac{\displaystyle \frac{\hbar^2}{2m} \left(\frac{I}{V}\ri...
...{u/u_0}{\,\rm d}(u/u_0)}{e^{u_0[(u/u_0)-1]}+ 1}
\right)^{2/3}
\end{displaymath}](img2559.gif)
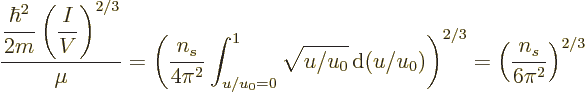
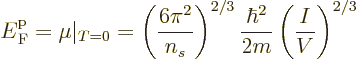
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]() ,
,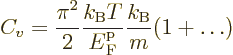
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]() :
:![\begin{displaymath}
-\frac{\mu}{{k_{\rm B}}T}
=
{\textstyle\frac{3}{2}}
\ln
...
...c{\hbar^2}{2m}\right.
\left(\frac{I}{V}\right)^{2/3}
\right]
\end{displaymath}](img2580.gif)
![]() .
.![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]() .
.![]() ,
,![]() .
.![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]() ,
,