| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
Subsections
1.3 Relativistic Mechanics
1.3.1 Intro to relativistic mechanics
Nonrelativistic mechanics is often based on the use of a potential
energy to describe the forces. For example, in a typical molecular
dynamics computation, the forces between the molecules are derived
from a potential that depends on the differences in position between
the atoms. Unfortunately, this sort of description fails badly in the
truly relativistic case.
The basic problem is not difficult to understand. If a potential
depends only on the spatial configuration of the atoms involved, then
the motion of an atom instantaneously affects all the other ones.
Relativity simply cannot handle instantaneous effects; they must be
limited by the speed of light or major problems appear. It makes
relativistic mechanics more difficult.
The simplest way to deal with the problem is to look at collisions
between particles. Direct collisions inherently avoid erroneous
action at a distance. They allow simple dynamics to be done without
the use of a potential between particles that is relativistically
suspect.
Figure 1.3:
Example elastic collision seen by different observers.
![\begin{figure}\centering
\setlength{\unitlength}{1pt}
\begin{picture}(405,52...
...f
\put(0,-20){\makebox(0,0)[b]{.}}
\end{picture} }
\end{picture}
\end{figure}](img130.gif) |
As a first example, consider two particles of equal mass and opposite
speeds that collide as shown in the center of figure
1.3. You might think of the particles as two helium
atoms. It will be assumed that while the speed of the atoms may be
quite high, the collision is at a shallow enough angle that it does
not excite the atoms. In other words, it is assumed that the
collision is elastic.
As seen by observer C, the collision is perfectly symmetric.
Regardless of the mechanics of the actual collision, observer C sees
nothing wrong with it. The energy of the helium atoms is the same
after the collision as before. Also, the net linear momentum was zero
before the collision and still zero afterwards. And whatever little
angular momentum there is, it too is still the same after the
collision.
But now consider an observer A that moves horizontally along with the
top helium atom. For this observer, the top helium atom comes down
vertically and bounces back vertically. Observer B moves along with
the bottom helium atom in the horizontal direction and sees that atom
moving vertically. Now consider the Lorentz transformation
(1.7) of the vertical velocity 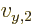 of the top atom
as seen by observer A into the vertical velocity
of the top atom
as seen by observer A into the vertical velocity  of that atom as
seen by observer B:
of that atom as
seen by observer B:
They are different! In particular,  is smaller than
is smaller than
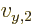 . Therefore, if the masses of the helium atoms that
the observers perceive would be their rest mass, linear momentum would
not be conserved. For example, observer A would perceive a net
downwards linear momentum before the collision and a net upwards
linear momentum after it.
. Therefore, if the masses of the helium atoms that
the observers perceive would be their rest mass, linear momentum would
not be conserved. For example, observer A would perceive a net
downwards linear momentum before the collision and a net upwards
linear momentum after it.
Clearly, linear momentum conservation is too fundamental a concept to
be summarily thrown out. Instead, observer A perceives the mass of the
rapidly moving lower atom to be the moving mass 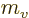 , which is
larger than the rest mass
, which is
larger than the rest mass  by the Lorentz factor:
by the Lorentz factor:
and that exactly compensates for the lower vertical velocity in the
expression for the momentum. (Remember that it was assumed that the
collision is under a shallow angle, so the vertical velocity
components are too small to have an effect on the masses.)
It is not difficult to understand why things are like this. The
nonrelativistic definition of momentum allows two plausible
generalizations to the relativistic case:
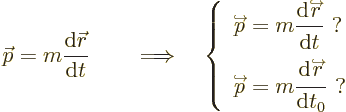
Indeed, nonrelativistically, all observers agree about time intervals.
However, relativistically the question arises whether the right time
differential in momentum is 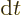 as perceived by the observer, or
the proper time difference
as perceived by the observer, or
the proper time difference 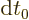 as perceived by a hypothetical
second observer moving along with the particle.
as perceived by a hypothetical
second observer moving along with the particle.
A little thought shows that the right time differential has to be
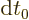 . For, after collisions the sum of the momenta should
be the same as before them. However, the Lorentz velocity
transformation (1.7) shows that perceived velocities
transform nonlinearly from one observer to the next. For a nonlinear
transformation, there is no reason to assume that if the momenta after
a collision are the same as before for one observer, they are also so
for another observer. On the other hand, since all observers agree
about the proper time intervals, momentum based on the proper time
interval
. For, after collisions the sum of the momenta should
be the same as before them. However, the Lorentz velocity
transformation (1.7) shows that perceived velocities
transform nonlinearly from one observer to the next. For a nonlinear
transformation, there is no reason to assume that if the momenta after
a collision are the same as before for one observer, they are also so
for another observer. On the other hand, since all observers agree
about the proper time intervals, momentum based on the proper time
interval 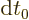 transforms like
transforms like ![${\rm d}\kern-1pt{\buildrel\raisebox{-1.5pt}[0pt][0pt]
{\hbox{\hspace{1pt}$\scriptscriptstyle\hookrightarrow$\hspace{0pt}}}\over r}
\kern-1.3pt$](img138.gif) , like position,
and that is linear. A linear transformation does assure that if an
observer A perceives that the sum of the momenta of a collection of
particles
, like position,
and that is linear. A linear transformation does assure that if an
observer A perceives that the sum of the momenta of a collection of
particles 
 1,2,...is the same before and after,
1,2,...is the same before and after,
then so does any other observer B:
Using the chain rule of differentiation, the components of
the momentum four-vector ![$\kern-1pt{\buildrel\raisebox{-1.5pt}[0pt][0pt]
{\hbox{\hspace{1pt}$\scriptscriptstyle\hookrightarrow$\hspace{0pt}}}\over p}
\kern-1.3pt$](img142.gif) can be written out as
can be written out as
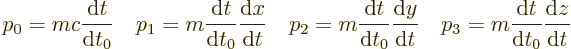 |
(1.14) |
The components 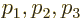 can be written in the same form as in the
nonrelativistic case by defining a moving mass
can be written in the same form as in the
nonrelativistic case by defining a moving mass
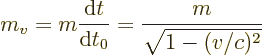 |
(1.15) |
How about the zeroth component? Since it too is part of the
conservation law, reasonably speaking it can only be the relativistic
equivalent of the nonrelativistic kinetic energy. Indeed, it equals
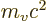 except for a trivial scaling factor 1
except for a trivial scaling factor 1
 to give it units of
momentum.
to give it units of
momentum.
Figure 1.4:
A completely inelastic collision.
![\begin{figure}\centering
\setlength{\unitlength}{1pt}
\begin{picture}(405,59...
...x(0,0)[r]{$M$}}
\put(330,10){\vector(0,-1){12}}
\end{picture}\par\end{figure}](img146.gif) |
Note that so far, this only indicates that the difference between
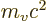 and
and 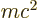 gives the kinetic energy. It does not imply that
gives the kinetic energy. It does not imply that
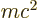 by itself also corresponds to a meaningful energy. However,
there is a beautifully simple argument to show that indeed kinetic
energy can be converted into rest mass, [21]. Consider
two identical rest masses
by itself also corresponds to a meaningful energy. However,
there is a beautifully simple argument to show that indeed kinetic
energy can be converted into rest mass, [21]. Consider
two identical rest masses  that are accelerated to high speed and
then made to crash into each other head-on, as in the left part of
figure 1.4. In this case, think of the masses as
macroscopic objects, so that thermal energy is a meaningful concept
for them. Assume that the collision has so much energy that the
masses melt and merge without any rebound. By symmetry, the combined
mass
that are accelerated to high speed and
then made to crash into each other head-on, as in the left part of
figure 1.4. In this case, think of the masses as
macroscopic objects, so that thermal energy is a meaningful concept
for them. Assume that the collision has so much energy that the
masses melt and merge without any rebound. By symmetry, the combined
mass  has zero velocity. Momentum is conserved: the net momentum
was zero before the collision because the masses had opposite
velocity, and it is still zero after the collision. All very
straightforward.
has zero velocity. Momentum is conserved: the net momentum
was zero before the collision because the masses had opposite
velocity, and it is still zero after the collision. All very
straightforward.
But now consider the same collision from the point of view of a second
observer who is moving upwards slowly compared to the first observer
with a small speed 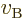 . No relativity involved here at
all; going up so slowly, the second observer sees almost the same
thing as the first one, with one difference. According to the second
observer, the entire collision process seems to have a small downward
velocity
. No relativity involved here at
all; going up so slowly, the second observer sees almost the same
thing as the first one, with one difference. According to the second
observer, the entire collision process seems to have a small downward
velocity 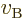 . The two masses have a slight downward
velocity
. The two masses have a slight downward
velocity 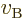 before the collision and so has the mass
before the collision and so has the mass  after the collision. But then vertical momentum conservation
inevitably implies
after the collision. But then vertical momentum conservation
inevitably implies
So  must be twice the moving mass
must be twice the moving mass 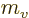 . The combined rest
mass
. The combined rest
mass  is not the sum of the rest masses
is not the sum of the rest masses  , but of
the moving masses
, but of
the moving masses 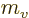 . All the kinetic energy given to
the two masses has ended up as additional rest mass in
. All the kinetic energy given to
the two masses has ended up as additional rest mass in  .
.
1.3.2 Lagrangian mechanics
Lagrangian mechanics can simplify many complicated dynamics problems.
As an example, in this section it is used to derive the relativistic
motion of a particle in an electromagnetic field.
Consider first the nonrelativistic motion of a particle in an
electrostatic field. That is an important case for this book, because
it is a good approximation for the electron in the hydrogen atom. To
describe such purely nonrelativistic motion, physicists like to define
a Lagrangian as
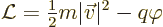 |
(1.16) |
where  is the mass of the particle,
is the mass of the particle,  its velocity, and
its velocity, and  its charge, while
its charge, while 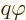 is the potential energy due to the
electrostatic field, which depends on the position of the particle.
(It is important to remember that the Lagrangian should mathematically
be treated as a function of velocity and position of the particle.
While for a given motion, the position and velocity are in turn
functions of time, time derivatives must be implemented through the
chain rule, i.e. by means of total derivatives of the Lagrangian.)
is the potential energy due to the
electrostatic field, which depends on the position of the particle.
(It is important to remember that the Lagrangian should mathematically
be treated as a function of velocity and position of the particle.
While for a given motion, the position and velocity are in turn
functions of time, time derivatives must be implemented through the
chain rule, i.e. by means of total derivatives of the Lagrangian.)
Physicists next define canonical, or generalized, momentum as the
partial derivative of the Lagrangian with respect to velocity. An
arbitrary component 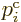 of the canonical momentum is found as
of the canonical momentum is found as
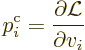 |
(1.17) |
This works out to be simply component 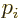

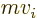 of the normal
momentum. The equations of motion are taken to be
of the normal
momentum. The equations of motion are taken to be
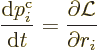 |
(1.18) |
which is found to be
That is simply Newton’s second law; the left hand side is just
mass times acceleration while in the right hand side minus the spatial
derivative of the potential energy gives the force. It can also be
seen that the sum of kinetic and potential energy of the particle
remains constant, by multiplying Newton’s equation by 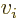 and
summing over
and
summing over  .
.
Since the Lagrangian is a just a scalar, it is relatively simple to
guess its form in the relativistic case. To get the momentum right,
simply replace the kinetic energy by an reciprocal Lorentz factor,
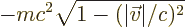
For velocities small compared to the speed of light, a two term Taylor
series shows this is equivalent to 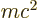 plus the kinetic energy.
The constant
plus the kinetic energy.
The constant 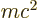 is of no importance since only derivatives of the
Lagrangian are used. For any velocity, big or small, the canonical
momentum as defined above produces the relativistic momentum based on
the moving mass as it should.
is of no importance since only derivatives of the
Lagrangian are used. For any velocity, big or small, the canonical
momentum as defined above produces the relativistic momentum based on
the moving mass as it should.
The potential energy part of the Lagrangian is a bit trickier. The
previous section showed that momentum is a four-vector including
energy. Therefore, going from one observer to another mixes up energy
and momentum nontrivially, just like it mixes up space and time. That
has consequences for energy conservation. In the classical solution,
kinetic energy of the particle can temporarily be stored away as
electrostatic potential energy and recovered later intact. But
relativistically, the kinetic energy seen by one observer becomes
momentum seen by another one. If that momentum is to be recovered
intact later, there should be something like potential momentum.
Since momentum is a vector, obviously so should potential momentum be:
there must be something like a vector potential  .
.
Based on those arguments, you might guess that the Lagrangian should
be something like
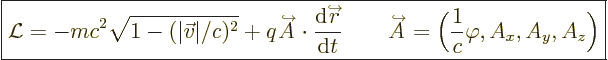 |
(1.19) |
And that is in fact right. Component zero of the potential
four-vector is the classical electrostatic potential. The spatial
vector 

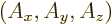 is called the “magnetic vector
potential.”
is called the “magnetic vector
potential.”
The canonical momentum is now
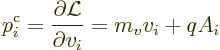 |
(1.20) |
and that is no longer just the normal momentum, 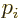

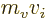 , but includes the magnetic vector potential.
, but includes the magnetic vector potential.
The Lagrangian equations of motion become, the same way as before, but
after clean up and in vector notation, {D.6}:
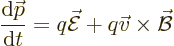 |
(1.21) |
The right-hand side in this equation of motion is called the Lorentz
force. In it,  is called the electric field and
is called the electric field and 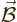 the magnetic field. These fields are related to the four-vector
potential as
the magnetic field. These fields are related to the four-vector
potential as
where by definition
is the vector operator called nabla or del.
Of course, if the Lagrangian above is right, it should apply to all
observers, regardless of their relative motion. In particular, all
observers should agree that the so-called action
integral 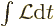 is stationary for the way that the particle
moves, {A.1.3}, {D.3.1} That
requires that
is stationary for the way that the particle
moves, {A.1.3}, {D.3.1} That
requires that ![${\buildrel\raisebox{-1.5pt}[0pt][0pt]
{\hbox{\hspace{2.5pt}$\scriptscriptstyle\hookrightarrow$\hspace{0pt}}}\over A}$](img174.gif) transforms according to the Lorentz
transformation.
transforms according to the Lorentz
transformation.
(To see why, recall that dot products are the same for all observers,
and that the square root in the Lagrangian (1.19) equals
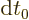

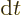 where the proper time interval
where the proper time interval 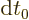 is the
same for all observers. So the action is the same for all observers.)
is the
same for all observers. So the action is the same for all observers.)
From the Lorentz transformation of ![${\buildrel\raisebox{-1.5pt}[0pt][0pt]
{\hbox{\hspace{2.5pt}$\scriptscriptstyle\hookrightarrow$\hspace{0pt}}}\over A}$](img174.gif) , that of the electric
and magnetic fields may be found; that is not a Lorentz
transformation. Note that this suggests that
, that of the electric
and magnetic fields may be found; that is not a Lorentz
transformation. Note that this suggests that ![${\buildrel\raisebox{-1.5pt}[0pt][0pt]
{\hbox{\hspace{2.5pt}$\scriptscriptstyle\hookrightarrow$\hspace{0pt}}}\over A}$](img174.gif) might be more
fundamental physically than the more intuitive electric and magnetic
fields. And that is in fact exactly what more advanced quantum
mechanics shows, chapter 13.1.
might be more
fundamental physically than the more intuitive electric and magnetic
fields. And that is in fact exactly what more advanced quantum
mechanics shows, chapter 13.1.
It may be noted that the field strengths are unchanged in a “gauge transformation” that modifies  and
and  into
into
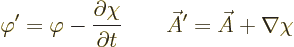 |
(1.22) |
where 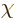 is any arbitrary function of position and time. This
might at first seem no more than a neat mathematical trick. But
actually, in advanced quantum mechanics it is of decisive importance,
chapter 7.3, {A.19.5}.
is any arbitrary function of position and time. This
might at first seem no more than a neat mathematical trick. But
actually, in advanced quantum mechanics it is of decisive importance,
chapter 7.3, {A.19.5}.
The energy can be found following addendum {A.1} as
The Hamiltonian is the energy expressed in terms of the canonical
momentum  instead of
instead of  ; that works out
to
; that works out
to
using the formula given in the overview subsection. The Hamiltonian
is of great importance in quantum mechanics.
![]()
![]()
![]() ,
,![]()
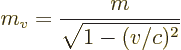

![]() .
.![]()
![]() ,
,![]()
![]()
![\begin{displaymath}
\sum_j \kern-1pt{\buildrel\raisebox{-1.5pt}[0pt][0pt]
{\hbo...
...ightarrow$\hspace{0pt}}}\over p}
\kern-1.3pt_{jA,{\rm before}}
\end{displaymath}](img140.gif)

![]()
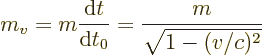
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]() .
.![]()
![]()
![]()
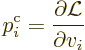
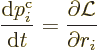
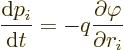
![]() .
.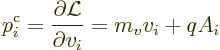
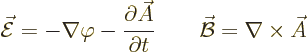
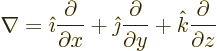
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()