1.1 Overview of Rel­a­tiv­ity

1.1.1 A note on the his­tory of the the­ory

Spe­cial rel­a­tiv­ity is com­monly at­trib­uted to Al­bert Ein­stein’s 1905 pa­pers. That is cer­tainly jus­ti­fi­able. How­ever, Ein­stein swiped the big ideas of rel­a­tiv­ity from Henri Poin­caré, (who de­vel­oped and named the prin­ci­ple of rel­a­tiv­ity in 1895 and a mass-en­ergy re­la­tion in 1900), with­out giv­ing him any credit or even men­tion­ing his name.

He may also have swiped the un­der­ly­ing math­e­mat­ics he used from Lorentz, (who is men­tioned, but not in con­nec­tion with the Lorentz trans­for­ma­tion.) How­ever, in case of Lorentz, it is pos­si­ble to be­lieve that Ein­stein was un­aware of his ear­lier work, if you are so trust­ing. Be­fore you do, it must be pointed out that a re­view of Lorentz’ 1904 work ap­peared in the sec­ond half of Feb­ru­ary 1905 in Beiblätter zu den An­nalen der Physik. Ein­stein was well aware of that jour­nal, since he wrote 21 re­views for it him­self in 1905. Sev­eral of these were in the very next is­sue af­ter the one with the Lorentz re­view, in the first half of March. Ein­stein’s first pa­per on rel­a­tiv­ity was re­ceived June 30 1905 and pub­lished Sep­tem­ber 26 in An­nalen der Physik. Ein­stein had been reg­u­larly writ­ing pa­pers for An­nalen der Physik since 1901. You do the math.

In case of Poin­caré, it is known that Ein­stein and a friend pored over Poin­caré’s 1902 book “Sci­ence and Hy­poth­e­sis.” In fact the friend noted that it kept them breath­less for weeks on end. So Ein­stein can­not pos­si­bly have been un­aware of Poin­caré’s work.

How­ever, Ein­stein should not just be blamed for his bold­ness in swip­ing most of the ideas in his pa­per from then more fa­mous au­thors, but also be com­mended for his bold­ness in com­pletely aban­don­ing the ba­sic premises of New­ton­ian me­chan­ics, where ear­lier au­thors wa­vered.

It should also be noted that gen­eral rel­a­tiv­ity can surely be cred­ited to Ein­stein fair and square. But he was a lot less hun­gry then. And had a lot more false starts. (There is a pos­si­bil­ity that the math­e­mati­cian Hilbert may have some par­tial claim on com­plet­ing gen­eral rel­a­tiv­ity, but it is clearly Ein­stein who de­vel­oped it. In fact, Hilbert wrote in one pa­per that his dif­fer­en­tial equa­tions seemed to agree with the “mag­nif­i­cent the­ory of gen­eral rel­a­tiv­ity es­tab­lished by Ein­stein in his later pa­pers.” Clearly then, Hilbert him­self agreed that Ein­stein es­tab­lished gen­eral rel­a­tiv­ity.)

1.1.2 The mass-en­ergy re­la­tion

The most im­por­tant re­sult of rel­a­tiv­ity for the rest of this book is with­out doubt Ein­stein’s fa­mous re­la­tion $E$ $\vphantom0\raisebox{1.5pt}{$=$}$ $mc^2$. Here $E$ is en­ergy, $m$ mass, and $c$ the speed of light. (A very lim­ited ver­sion of this re­la­tion was given be­fore Ein­stein by Poin­caré.)

The re­la­tion im­plies that the ki­netic en­ergy of a par­ti­cle is not $\frac12mv^2$, with $m$ the mass and $v$ the ve­loc­ity, as New­ton­ian physics would have it. In­stead the ki­netic en­ergy is the dif­fer­ence be­tween the en­ergy $m_vc^2$ based on the mass $m_v$ of the par­ti­cle in mo­tion and the en­ergy $mc^2$ based on the mass $m$ of the same par­ti­cle at rest. Ac­cord­ing to spe­cial rel­a­tiv­ity the mass in mo­tion is re­lated to the mass at rest as

$$m_v=\frac{m}{\sqrt{1-(v/c)^2}} %$$ (1.1)

There­fore the true ki­netic en­ergy can be writ­ten as

$$T = \frac{m}{\sqrt{1 - (v/c)^2}} c^2 - m c^2$$

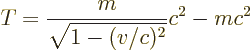
For ve­loc­i­ties small com­pared to the tremen­dous speed of light, this is equiv­a­lent to the clas­si­cal $\frac12mv^2$. That can be seen from Tay­lor se­ries ex­pan­sion of the square root. But when the par­ti­cle speed ap­proaches the speed of light, the above ex­pres­sion im­plies that the ki­netic en­ergy ap­proaches in­fin­ity. Since there is no in­fi­nite sup­ply of en­ergy, the ve­loc­ity of a ma­te­r­ial ob­ject must al­ways re­main less than the speed of light.

The pho­tons of elec­tro­mag­netic ra­di­a­tion, (which in­cludes ra­dio waves, mi­crowaves, light, x-rays, gamma rays, etcetera), do travel at the speed of light through a vac­uum. How­ever, the only rea­son that they can do so is be­cause they have zero rest mass $m$. There is no way that pho­tons in vac­uum can be brought to a halt, or even slowed down, be­cause there would be noth­ing left.

If the ki­netic en­ergy is the dif­fer­ence be­tween $m_vc^2$ and $mc^2$, then both of these terms must have units of en­ergy. That does of course not prove that each term is a phys­i­cally mean­ing­ful en­ergy by it­self. But it does look plau­si­ble. It sug­gests that a par­ti­cle at rest still has a rest mass en­ergy $mc^2$ left. And so it turns out to be. For ex­am­ple, an elec­tron and a positron can com­pletely an­ni­hi­late each other, re­leas­ing their rest mass en­er­gies as two pho­tons that fly apart in op­po­site di­rec­tions. Sim­i­larly, a pho­ton of elec­tro­mag­netic ra­di­a­tion with enough en­ergy can cre­ate an elec­tron-positron pair out of noth­ing. (This does re­quire that a heavy nu­cleus is around to ab­sorb the pho­ton’s lin­ear mo­men­tum with­out ab­sorb­ing too much of its en­ergy; oth­er­wise it would vi­o­late mo­men­tum con­ser­va­tion.) Per­haps more im­por­tantly for en­gi­neer­ing ap­pli­ca­tions, the en­ergy re­leased in nu­clear re­ac­tions is pro­duced by a re­duc­tion in the rest masses of the nu­clei in­volved.

Quan­tum me­chan­ics does not use the speed $v$ of a par­ti­cle, but its mo­men­tum $p$ $\vphantom0\raisebox{1.5pt}{$=$}$ $m_vv$. In those terms the to­tal en­ergy, ki­netic plus rest mass en­ergy, can be rewrit­ten as

$$\fbox{$\displaystyle E = T + mc^2 = \sqrt{(mc^2)^2 + p^2c^2} $} %$$ (1.2)

This ex­pres­sion is read­ily checked by sub­sti­tut­ing in for $p$, then for $m_v$, and clean­ing up.

1.1.3 The uni­ver­sal speed of light

The key dis­cov­ery of rel­a­tiv­ity is that the ob­served speed of light through vac­uum is the same re­gard­less of how fast you are trav­el­ing. One his­tor­i­cal step that led to this dis­cov­ery was a fa­mous ex­per­i­ment by Michel­son & Mor­ley. In sim­pli­fied terms, Michel­son & Mor­ley tried to de­ter­mine the ab­solute speed of the earth through space by horse-rac­ing it against light. If a pas­sen­ger jet air­plane flies at three quar­ters of the speed of sound, then sound waves go­ing in the same di­rec­tion as the plane only have a speed ad­van­tage of one quar­ter of the speed of sound over the plane. Seen from in­side the plane, that sound seems to move away from it at only a quar­ter of the nor­mal speed of sound.

Es­sen­tially, Michel­son & Mor­ley rea­soned that the speed of the earth could sim­i­larly be ob­served by mea­sur­ing how much it re­duces the ap­par­ent speed of light mov­ing in the same di­rec­tion through a vac­uum. But it proved that the mo­tion of the earth pro­duced no re­duc­tion in the ap­par­ent speed of light what­so­ever. It is as if you are rac­ing a fast horse, but re­gard­less of how fast you are go­ing, you do not re­duce the ve­loc­ity dif­fer­ence any more than if you would just stop your horse and have a drink.

The sim­plest ex­pla­na­tion would be that earth is at rest com­pared to the uni­verse. But that can­not pos­si­bly be true. Earth is a mi­nor planet in an outer arm of the galaxy. And earth moves around the sun once a year. Ob­vi­ously, the en­tire uni­verse could not pos­si­bly fol­low that non­in­er­tial mo­tion.

So how come that earth still seems to be at rest com­pared to light waves mov­ing through vac­uum? You can think up a hun­dred ex­cuses. In par­tic­u­lar, the sound in­side a plane does not seem to move any slower in the di­rec­tion of mo­tion. But of course, sound is trans­mit­ted by real air mol­e­cules that can be trapped in­side a plane by well es­tab­lished mech­a­nisms. It is not trans­mit­ted through empty space like light.

But then, at the time of the Michel­son & Mor­ley ex­per­i­ment the pre­vail­ing the­ory was that light did move through some hy­po­thet­i­cal medium. This made-up medium was called the ether. It was sup­pos­edly maybe dragged along by the earth, or maybe dragged along a bit, or maybe not af­ter all. In fact, Michel­son & Mor­ley were re­ally try­ing to de­cide how much it was be­ing dragged along. Look­ing back, it seems self-ev­i­dent that this ether was an un­sub­stan­ti­ated the­ory full of holes. But at the time most sci­en­tists took it very se­ri­ously.

The re­sults of the Michel­son & Mor­ley ex­per­i­ment and oth­ers upped the ante. To what could rea­son­ably be taken to be ex­per­i­men­tal er­ror, the earth did not seem to move rel­a­tive to light waves in vac­uum. So in 1895 Poin­caré rea­soned that ex­per­i­ments like the one of Michel­son & Mor­ley sug­gested that it is im­pos­si­ble to de­tect ab­solute mo­tion. In 1900 he pro­posed the Prin­ci­ple of Rel­a­tive Mo­tion. It pro­posed that the laws of move­ment would be the same in all co­or­di­nate sys­tems re­gard­less of their ve­loc­ity, as long as they are not ac­cel­er­at­ing. In 1902, in the book read by Ein­stein, he dis­cussed philo­soph­i­cal as­sess­ments on the rel­a­tiv­ity of space, time, and si­mul­tane­ity, and the idea that a vi­o­la­tion of the rel­a­tiv­ity prin­ci­ple can never be de­tected. In 1904 he called it

“The prin­ci­ple of rel­a­tiv­ity, ac­cord­ing to which the laws of phys­i­cal phe­nom­ena must be the same for a sta­tion­ary ob­server as for one car­ried along in a uni­form mo­tion of trans­la­tion, so that we have no means, and can have none, of de­ter­min­ing whether or not we are be­ing car­ried along in such a mo­tion.”

In short, if two ob­servers are mov­ing at dif­fer­ent, but con­stant speeds, it is im­pos­si­ble to say which one, if any, is at rest. The laws of physics ob­served by the two ob­servers are ex­actly the same. In par­tic­u­lar, the

mov­ing ob­servers see the same speed of light re­gard­less of their dif­fer­ent phys­i­cal mo­tion.

(Do note how­ever that if an ob­server is ac­cel­er­at­ing or spin­ning around, that can be de­ter­mined through the gen­er­ated in­er­tia forces. Not all mo­tion is rel­a­tive. Just an im­por­tant sub­set of it.)

A cou­ple of ad­di­tional his­tor­i­cal notes may be ap­pro­pri­ate. Quite a num­ber of his­to­ri­ans of sci­ence ar­gue that Poin­caré did not re­ally pro­pose rel­a­tiv­ity, be­cause he con­tin­ued to use the ether in var­i­ous com­pu­ta­tions af­ter­wards. This ar­gu­ment is un­jus­ti­fied. To this very day, the over­whelm­ing ma­jor­ity of physi­cists and en­gi­neers still use New­ton­ian physics in their com­pu­ta­tions. That does not mean that these physi­cists and en­gi­neers do not be­lieve in spe­cial rel­a­tiv­ity. It means that they find do­ing the New­ton­ian com­pu­ta­tion a lot eas­ier, and it gives the right an­swer for their ap­pli­ca­tions. Sim­i­larly, Poin­caré him­self clearly stated that he still con­sid­ered the ether a “con­ve­nient hy­poth­e­sis.” There were well es­tab­lished pro­ce­dures for com­put­ing such things as the prop­a­ga­tion of light in mov­ing me­dia us­ing an as­sumed ether that had been well ver­i­fied by ex­per­i­ment.

A more in­ter­est­ing hy­poth­e­sis ad­vanced by his­to­ri­ans is that Ein­stein may have been more in­clined to do away with the ether from the start than other physi­cists. The con­cept of the ether was with­out doubt sig­nif­i­cantly mo­ti­vated by the prop­a­ga­tion of other types of waves like sound waves and wa­ter waves. In such waves, there is some ma­te­r­ial sub­stance that per­forms a wave mo­tion. Un­like waves, how­ever, par­ti­cles of all kinds read­ily prop­a­gate through empty space; they do not de­pend on a sep­a­rate medium that waves. That did not seem rel­e­vant to light, be­cause its wave-like na­ture had been well es­tab­lished. But in quan­tum me­chan­ics, the com­ple­men­tary na­ture of light as par­ti­cles called pho­tons was emerg­ing. And Ein­stein may have been more com­fort­able with the quan­tum me­chan­i­cal con­cept of light than most at the time. He was a ma­jor de­vel­oper of it.

1.1.4 Dis­agree­ments about space and time

At first, it may not seem such a big deal that the speed of light is the same re­gard­less of the mo­tion of the ob­server. But when this no­tion is ex­am­ined in some more de­tail, it leads to some very counter-in­tu­itive con­clu­sions.

It turns out that if ob­servers are in mo­tion com­pared to each other, they will un­avoid­ably dis­agree about such things as spa­tial dis­tances and the time that things take. Of­ten, dif­fer­ent ob­servers can­not even agree on which of two phys­i­cal events takes place ear­lier than the other. As­sum­ing that they de­ter­mine the times cor­rectly in their own co­or­di­nate sys­tem, they will come up with dif­fer­ent an­swers.

Self-ev­i­dently, if ob­servers can­not even agree on which of two events hap­pened first, then an ab­solute time scale that every­one can agree on is not pos­si­ble ei­ther. And nei­ther is a sys­tem of ab­solute spa­tial co­or­di­nates that every­body can agree upon.

Fig­ure 1.1: Dif­fer­ent views of the same ex­per­i­ment. Left is the view of ob­servers on the plan­ets. Right is the view of an alien space ship.

Con­sider a ba­sic thought ex­per­i­ment. A thought ex­per­i­ment is an ex­per­i­ment that should in prin­ci­ple be pos­si­ble, but you do not want to be in charge of ac­tu­ally do­ing it. Sup­pose that the plan­ets Venus and Mars hap­pen to be at op­po­site sides of earth, and at roughly the same dis­tance from it. The left side of fig­ure 1.1 shows the ba­sic idea. Ex­per­i­menters on earth flash si­mul­ta­ne­ous light waves at each planet. Since Venus hap­pens to be a bit closer than Mars, the light hits Venus first. All very straight­for­ward. Ob­servers on Venus and Mars would agree com­pletely with ob­servers on earth that Venus got hit first. They also agree with earth about how many min­utes it took for the light to hit Venus and Mars.

To be sure, the plan­ets move with speeds of the or­der of 100,000 mph rel­a­tive to one an­other. But that speed, while very large in hu­man terms, is so small com­pared to the tremen­dous speed of light that it can be ig­nored. For the pur­poses of this dis­cus­sion, it can be as­sumed that the plan­ets are at rest rel­a­tive to earth.

Next as­sume that a space ship with aliens was just pass­ing by and watched the whole thing, like in the right half of fig­ure 1.1. As seen by ob­servers on earth, the aliens are mov­ing to the right with half the speed of light. How­ever, the aliens can ar­gue that it is they that are at rest, and that the three plan­ets are mov­ing to­wards the left with half the speed of light. Ac­cord­ing to the prin­ci­ple of rel­a­tiv­ity, both points of view are equally valid. There is noth­ing that can show whether the space ship or the plan­ets are at rest, or nei­ther one.

In par­tic­u­lar, the speed of the light waves that the aliens ob­serve is iden­ti­cal to the speed that earth sees. But now note that as far as the aliens are con­cerned, Venus moves with half the speed of light away from its in­com­ing light wave. Of course, that sig­nif­i­cantly in­creases the time that the light needs to reach Venus. On the other hand, the aliens see Mars mov­ing at half the speed of light to­wards its in­com­ing light wave. That roughly halves the time needed for the light wave to hit Mars. In short, un­like earth, the aliens ob­serve that the light hits Mars a lot ear­lier than it hits Venus.

That ex­am­ple demon­strates that ob­servers in rel­a­tive mo­tion dis­agree about the time dif­fer­ence be­tween events oc­cur­ring at dif­fer­ent lo­ca­tions. Worse, even if two events hap­pen right in the hands of one of the ob­servers, the ob­servers will dis­agree about how long the en­tire thing takes. In that case, the ob­server com­pared to which the lo­ca­tion of the events is in mo­tion will think that it takes longer. This is called “time-di­la­tion.” The time dif­fer­ence be­tween two events slows down ac­cord­ing to

$$\fbox{$\displaystyle \Delta t_v = \frac{\Delta t_0}{\sqrt{1 - (v/c)^2}} $} %$$ (1.3)

Here $\Delta{t}_0$ is short­hand for the time dif­fer­ence be­tween the two events as seen by an ob­server com­pared to whom the two events oc­cur at the same lo­ca­tion. Sim­i­larly $\Delta{t}_v$ is the time dif­fer­ence be­tween the two events as per­ceived by an ob­server com­pared to whom the lo­ca­tion of the events is mov­ing at speed $v$.

An event can be any­thing with an un­am­bigu­ous phys­i­cal mean­ing, like when the hands of a clock reach a cer­tain po­si­tion. So clocks are found to run slow when they are in mo­tion com­pared to the ob­server. The best cur­rent clocks are ac­cu­rate enough to di­rectly mea­sure this ef­fect at hu­man-scale speeds, as low as 20 mph. But rel­a­tiv­ity has al­ready been ver­i­fied in myr­iad other ways. The time is long gone that se­ri­ous sci­en­tists still doubted the con­clu­sions of rel­a­tiv­ity.

As a more prac­ti­cal ex­am­ple, cos­mic rays can cre­ate ra­dioac­tive par­ti­cles in the up­per at­mos­phere that sur­vive long enough to reach the sur­face of the earth. The sur­pris­ing thing is that at rest in a lab­o­ra­tory these same par­ti­cles would not sur­vive that long by far. The par­ti­cles cre­ated by cos­mic rays have ex­tremely high speed when seen by ob­servers stand­ing on earth. That slows down the de­cay process due to time di­la­tion.

Which of course raises the ques­tion: should then not an ob­server mov­ing along with one such par­ti­cle ob­serve that the par­ti­cle does not reach the earth? The an­swer is no; rel­a­tiv­ity main­tains a sin­gle re­al­ity; a par­ti­cle ei­ther reaches the earth or not, re­gard­less of who is do­ing the ob­serv­ing. It is quan­tum me­chan­ics, not rel­a­tiv­ity, that does away with a sin­gle re­al­ity. The ob­server mov­ing with the par­ti­cle ob­serves that the par­ti­cle reaches the earth, not be­cause the par­ti­cle seems to last longer than usual, but be­cause the dis­tance to travel to the sur­face of the earth has be­come much shorter! This is called “Lorentz-Fitzger­ald con­trac­tion.”

For the ob­server mov­ing with the par­ti­cle, it seems that the en­tire earth sys­tem, in­clud­ing the at­mos­phere, is in mo­tion with al­most the speed of light. The size of ob­jects in mo­tion seems to con­tract in the di­rec­tion of the mo­tion ac­cord­ing to

$$\fbox{$\displaystyle \Delta x_v = \Delta x_0\sqrt{1 - (v/c)^2} $} %$$ (1.4)

Here the $x$-​axis is taken to be in the di­rec­tion of mo­tion. Also $\Delta{x}_0$ is the dis­tance in the x-di­rec­tion be­tween any two points as seen by an ob­server com­pared to whom the points are at rest. Sim­i­larly, $\Delta{x}_v$ is the dis­tance as seen by an ob­server com­pared to whom the points are mov­ing with speed $v$ in the $x$-​di­rec­tion.

In short, for the ob­server stand­ing on earth, the par­ti­cle reaches earth be­cause its mo­tion slows down the de­cay process by a fac­tor 1/$\sqrt{1-(v/c)^2}$. For the ob­server mov­ing along with the par­ti­cle, the par­ti­cle reaches earth be­cause the dis­tance to travel to the sur­face of the earth has be­come shorter by ex­actly that same fac­tor. The rec­i­p­ro­cal square root is called the “Lorentz fac­tor.”

Lorentz-Fitzger­ald con­trac­tion is also ev­i­dent in how the aliens see the plan­ets in fig­ure 1.1. But note that the dif­fer­ence in the wave lengths of the light waves is not a sim­ple mat­ter of Lorentz-Fitzger­ald con­trac­tion. The light waves are in mo­tion com­pared to both ob­servers, so Lorentz-Fitzger­ald con­trac­tion sim­ply does not ap­ply.

The cor­rect equa­tion that gov­erns the dif­fer­ence in ob­served wave length $\lambda$ of the light, and the cor­re­spond­ing dif­fer­ence in ob­served fre­quency $\omega$, is

$$\fbox{$\displaystyle \lambda_v = \lambda_0 \sqrt{\frac{1 +... ... \omega_v = \omega_0 \sqrt{\frac{1 - (v/c)}{1 + (v/c)}} $} %$$ (1.5)

Here the sub­script 0 stands for the emit­ter of the light, and sub­script $v$ for an ob­server mov­ing with speed $v$ away from the emit­ter. If the ob­server moves to­wards the emit­ter, $v$ is neg­a­tive. (To be true, the for­mu­lae above ap­ply whether the ob­server 0 is emit­ting the light or not. But in most prac­ti­cal ap­pli­ca­tions, ob­server 0 is in­deed the emit­ter.)

In terms of the ex­am­ple fig­ure 1.1, 0 in­di­cates the emit­ter earth, and $v$ in­di­cates the aliens ob­serv­ing the ra­di­a­tion. If the aliens are still to the left of earth, they are still clos­ing in on it and $v$ is neg­a­tive. Then the for­mu­lae above say that the wave length seen by the aliens is shorter than the one seen by earth. Also, the fre­quency seen by the aliens is higher than the one seen by earth, and so is the en­ergy of the light. When the aliens get to the right of earth, they are mov­ing away from it. That makes $v$ pos­i­tive, and the light from earth that is reach­ing them now seems to be of longer wave length, of lower fre­quency, and less en­er­getic. These changes are re­ferred to as Doppler shifts.

One re­lated ef­fect is cos­mic red­shift. The en­tire uni­verse is ex­pand­ing. As a re­sult, far away galax­ies move away from us at ex­tremely high speeds. That causes wave length shifts; the ra­di­a­tion emit­ted or ab­sorbed by var­i­ous ex­cited atoms in these galax­ies ap­pears to us to have wave lengths that are too long. The re­ceived wave lengths are longer than those that these same atoms would emit or ab­sorb on earth. In par­tic­u­lar, the col­ors of vis­i­ble light are shifted to­wards the red side of the spec­trum. To ob­servers in the galax­ies them­selves, how­ever, the col­ors would look per­fectly fine.

Note that the cos­mic red­shift can only qual­i­ta­tively be un­der­stood from the for­mu­lae above. It is more ac­cu­rate to say that the pho­tons trav­el­ing to us from re­mote galax­ies get stretched due to the ex­pan­sion of the uni­verse. The cos­mic red­shift is not due to the mo­tion of the galax­ies through space, but due to the mo­tion of space it­self. If the ex­pan­sion of space is rephrased in terms of a rel­a­tive ve­loc­ity of the galax­ies com­pared to us, that ve­loc­ity can ex­ceed the speed of light. That would pro­duce non­sense in the for­mu­lae above. Ob­jects can­not move faster than the speed of light through space, but the ve­loc­ity of dif­fer­ent re­gions of space com­pared to each other can ex­ceed the speed of light.

Re­turn­ing to the nor­mal Doppler shift, the changes in wave length are not di­rectly due to Lorentz-Fitzger­ald con­trac­tion. In­stead, they can in part be at­trib­uted to time di­la­tion. In fig­ure 1.1 both the aliens and earth can de­duce the wave length from how fre­quently the peaks of the wave leave the emit­ter earth. But in do­ing so, one source of dis­agree­ment is time di­la­tion. Since earth is in mo­tion com­pared to the aliens, the aliens think that the peaks leave earth less fre­quently than earth does. In ad­di­tion, the aliens and earth dis­agree about the rel­a­tive ve­loc­ity be­tween the light waves and earth. Earth thinks that the light waves leave with the speed of light rel­a­tive to earth. The aliens also think that the light waves travel with the speed of light, but in ad­di­tion they see earth mov­ing to­wards the left with half the speed of light. Com­bine the two ef­fects, for ar­bi­trary ve­loc­ity of the aliens, and the re­la­tion be­tween the wave lengths is as given above. Fur­ther, since the speed of light is the same for both earth and aliens, the ob­served fre­quency of the light is in­versely pro­por­tional to the ob­served wave length.